贵州省遵义市余庆县2024-2025学年九年级上学期11月期中考试数学试题

这是一份贵州省遵义市余庆县2024-2025学年九年级上学期11月期中考试数学试题，共11页。试卷主要包含了如图，，直线与分别相交于和，如图，矩形与反比例函数等内容，欢迎下载使用。
注意事项：
1．你拿到的试卷满分150分，考试时间为120分钟。
2．本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页，“答题卷”共6页。
3．请务必在“答题卷”上答题，在“试题卷”上答题是无效的。
4．考试结束后，请将“试题卷”和“答题卷”一并交回。
一、选择题（本大题共10小题，每小题4分，满分40分）
每小题都给出A、B、C、D四个选项，其中只有一个是正确的。
1．地图上淮北到合肥的距离为2.4厘米，比例尺是，那么淮北到合肥的实际距离是（ ）
A．2400米B．24000米C．240000米D．2400000米
2．若抛物线与的形状相同，则的值为（ ）
A．2B．3或C．1D．2或
3．如图，已知，那么添加下列一个条件后，仍无法判定的是（ ）
第3题图
A．B．C．D．
4．已知蓄电池的电压为定值，使用蓄电池时，电流（单位：A）与电阻（单位：）是反比例函数关系．下列反映电流与电阻之间函数关系的图象大致是（ ）
A．B．C．D．
5．如图，，直线与分别相交于和．若，，则的长是（ ）
第5题图
A．B．C．6D．10
6．如表给出了二次函数的自变量与函数值的部分对应值，那么方程的一个根的近似值可能是（ ）
A．1.09B．1.19C．1.29D．1.39
7．如图，是面积为的等边三角形，被一矩形所截，被截成三等分，，则图中阴影部分的面积为（ ）
第7题图
A．B．C．D．
8．如图，矩形与反比例函数（是非零常数，）的图象交于点，与反比例函数（是非零常数，）的图象交于点，连接，ON．若四边形的面积为3，则（ ）
第8题图
A．3B．C．D．
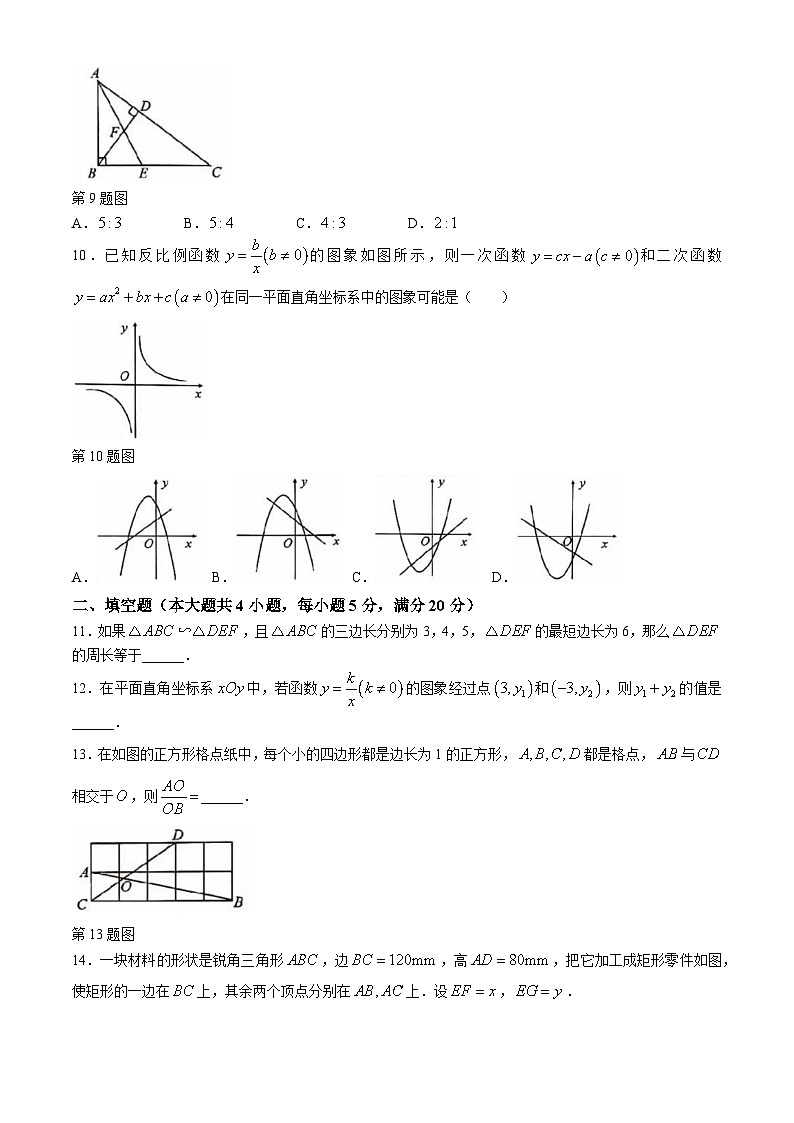
9．如图，中，，，垂足为，平分，分别交，于点．若，则为（ ）
第9题图
A．B．C．D．
10．已知反比例函数的图象如图所示，则一次函数和二次函数在同一平面直角坐标系中的图象可能是（ ）
第10题图
A．B．C．D．
二、填空题（本大题共4小题，每小题5分，满分20分）
11．如果，且的三边长分别为3，4，5，的最短边长为6，那么的周长等于______．
12．在平面直角坐标系中，若函数的图象经过点和，则的值是______．
13．在如图的正方形格点纸中，每个小的四边形都是边长为1的正方形，都是格点，与相交于，则______．
第13题图
14．一块材料的形状是锐角三角形，边，高，把它加工成矩形零件如图，使矩形的一边在上，其余两个顶点分别在上．设，．
第14题图
（1）______（用含的式子表示）；
（2）这个矩形的最大面积是______．
三、（本大题共2小题，每小题8分，满分16分）
15．已知，求的值．
16．已知二次函数．
第16题图
（1）画出这个函数的图象；
（2）根据图象，直接写出当时，的取值范围．
四、（本大题共2小题，每小题8分，满分16分）
17．如图，已知，，，，．求证：．
第17题图
18．“黄金三角形”是几何历史上的瑰宝，它有两种类型，其中一种是顶角为的等腰三角形，如图，在中，，．
第18题图
（1）利用尺规作的平分线，交边于点（要求：尺规作图并保留作图痕迹，不写作法，标明字母）；
（2）证明：．
五、（本大题共2小题，每小题10分，满分20分）
19．在校园科技节期间，科普员为同学们进行了水火箭的发射表演，图1是某型号水火箭的实物图，水火箭发射后的运动路线可以看作是一条抛物线．为了解水火箭的相关性能，同学们进一步展开研究．如图2建立直角坐标系，水火箭发射后落在水平地面处，科普员提供了该型号水火箭与地面成一定角度时，从发射到着陆过程中，水火箭距离地面的竖直高度与离发射点的水平距离的几组关系数据如下：
（1）根据表格，试确定抛物线的表达式；
（2）请计算当水火箭飞行至离发射点的水平距离为5m时，水火箭距离地面的竖直高度．
第19题图
20．已知菱形中，为的中点，交于，且．
第20题图
（1）求证：；
（2）若，求的长．
六、（本题满分12分）
21．如图，一次函数的图象与反比例函数的图象交于点、．
第21题图
（1）求反比例函数和一次函数的表达式；
（2）利用图象，直接写出不等式的解集；
（3）已知点在轴上，点在反比例函数图象上，若四边形是平行四边形，求点的坐标．
七、（本题满分12分）
22．定义：在平面直角坐标系中，抛物线与轴的交点坐标为，那么我们把经过点且平行于轴的直线称为这条抛物线的极限分割线．
【特例感知】
（1）抛物线的极限分割线与这条抛物线的交点坐标为______；
【深入探究】
（2）经过点和的抛物线与轴交于点，它的极限分割线与该抛物线的另一个交点为，请用含的代数式表示点的坐标；
【拓展运用】
（3）在（2）的条件下，设抛物线的顶点为，直线垂直平分，垂足为，交该抛物线的对称轴于点，，求点的坐标．
八、（本题满分14分）
23．如图，直角中，，在上，连接，作分别交于，于．
第23题图
（1）如图1，若，求证：；
（2）如图2，若，取的中点，连接交于，求证：
①；
②．
数学参考答案及评分标准
一、选择题（本大题共10小题，每小题4分，满分40分）
9．A ，设，，，，
，，，，，，，平分，，又，
．．故选A．
10．D 反比例函数的图象位于一、三象限，；、的抛物线都是开口向下，，根据同左异右，对称轴应该在轴的右侧，故A、B都是错误的．、的抛物线都是开口向上，，根据同左异右，对称轴应该在轴的左侧，抛物线与轴交于负半轴，，由，，排除C．故选D．
二、填空题（本大题共4小题，每小题5分，满分20分）
11．24 12．0 13．
14．（1） （2）2400
（1），，，；
（2）矩形面积，
故当时，此时矩形的面积最大，最大面积为．
三、（本大题共2小题，每小题8分，满分16分）
15．解：设，则，，，．
16．解：（1）已知二次函数，列表如下：
函数图像如下所示：
第16题答案图
（2）或．
四、（本大题共2小题，每小题8分，满分16分）
17．解：证明：，，，，，．
，，．
18．解：（1）如图所示，即为所求；
第18题答案图
（2）证明：在中，，，，
平分，，，，，，
，，，，，．
五、（本大题共2小题，每小题10分，满分20分）
19．解：（1）由题意可得，抛物线的对称轴是直线，
抛物线的顶点为，可设抛物线为．又抛物线过，．，抛物线的表达式为；
（2）由题意，结合（1），
令，则，水火箭距离地面的竖直高度为5m．
20．解：（1）证明：四边形是菱形，，，，
，，，，．
，为中点，，，；
（2）设，则，，
，，，，
，，（负值舍去），．
六、（本题满分12分）
21．解：（1）将点、的坐标代入反比例函数表达式得：，
解得：，，即反比例函数的表达式为：，点；
将点、的坐标代入一次函数表达式得：，解得：，
则一次函数表达式为：；
（2）或；
（3）设点的坐标为：，点，当为对角线时，由中点坐标公式得：，解得：，则点．
七、（本题满分12分）
22．解：（1）和．
（2）抛物线经过点，，．
，
对称轴为直线，点的坐标为；
（3）设与对称轴交于点，若．则．
，或．
当时，，点的坐标为；
当时，，点的坐标为，
点的坐标为或．
八、（本题满分14分）
23．解：（1）证明：在和中，，；
（2）①如图，过作交于，
，，，设，，，
，，；
②如图，过作交的延长线于．则．
，，由①知，，
，，
，，，，
，．
第23题答案图
…
1
1.1
1.2
1.3
1.4
…
…
1
0.49
…
水平距离
0
3
4
10
15
20
22
27
竖直高度
0
3.24
4.16
8
9
8
7.04
3.24
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
D
C
B
C
B
A
D
…
－1
0
1
2
3
…
…
0
2
0
…