

湖北省武汉市青山区2024-2025学年八年级上学期期中数学试题
展开
这是一份湖北省武汉市青山区2024-2025学年八年级上学期期中数学试题,共11页。试卷主要包含了11等内容,欢迎下载使用。
(请将答案写在答题卡上 满分:120分 时间:120分钟)
第Ⅰ卷(选择题,共30分)
一、选择题(共10小题,每小题3分,共30分)
下列各题有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.
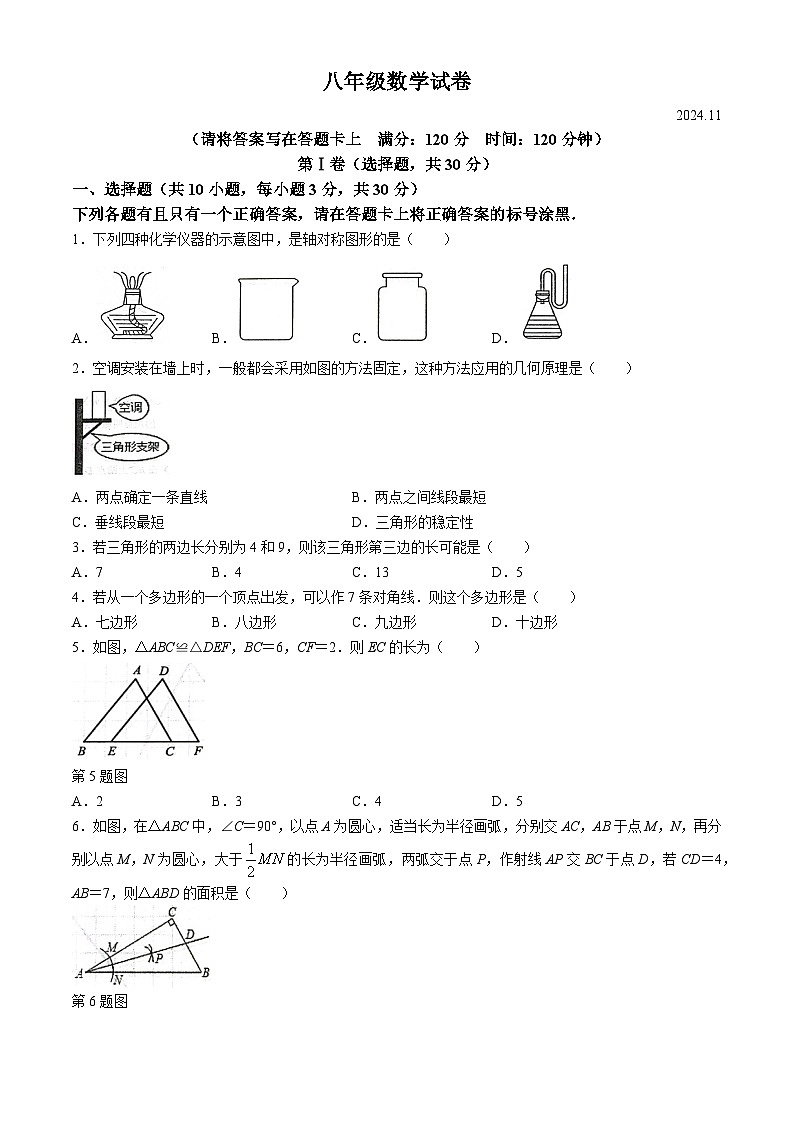
1.下列四种化学仪器的示意图中,是轴对称图形的是( )
A.B.C.D.
2.空调安装在墙上时,一般都会采用如图的方法固定,这种方法应用的几何原理是( )
A.两点确定一条直线B.两点之间线段最短
C.垂线段最短D.三角形的稳定性
3.若三角形的两边长分别为4和9,则该三角形第三边的长可能是( )
A.7B.4C.13D.5
4.若从一个多边形的一个顶点出发,可以作7条对角线.则这个多边形是( )
A.七边形B.八边形C.九边形D.十边形
5.如图,△ABC≌△DEF,BC=6,CF=2.则EC的长为( )
第5题图
A.2B.3C.4D.5
6.如图,在△ABC中,∠C=90°,以点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交BC于点D,若CD=4,AB=7,则△ABD的面积是( )
第6题图
A.5B.7C.14D.28
7.在如图的三角形纸片中,AB=8cm,BC=6cm,AC=5cm,沿过点B的直线折叠这个三角形,使点C落在边AB上的点E处,折痕为BD,则△AED的周长为( )
第7题图
A.5cmB.6cmC.7cmD.8cm
8.如图,在△ABC中,AB=BC,∠ABC=120°,AB的垂直平分线交AC于点D.若AC=9,则AD的长为( )
第8题图
A.2B.3C.4D.5
9.如图,∠ABD与∠ACD的角平分线交于点P,∠A=60°,∠D=10°,则∠P为( )
第9题图
A.30°B.25°C.20°D.15°
10.如图,在△ABC中,AB=AC,BC=6,,直线EF垂直平分线段AB,若点D为边BC的中点,点G为直线EF上一动点,则△BDG周长的最小值为( )
第10题图
A.12B.13C.10D.14
第Ⅱ卷(非选择题,共90分)
二、填空题(共6小题,每小题3分,共18分)
下列各题不需要写出解答过程,请将结论直接填写在答题卡的指定位置.
11.已知点P(a,2)和点Q(-4,b)关于x轴对称.则a+b=______.
12.若n边形的内角和与外角和相等.则n=______.
13.如图,点D在AB上,点E在AC上,AB=AC,请补充一个条件,使△ABE≌△ACD,你补充的条件是______.
第13题图
14.已知等腰三角形一个内角的度数为80°.则这个等腰三角形底角的度数为______.
15.如图,在△ABC中,∠ACB=36°,∠BAC=117°,过A作AD⊥BC于点D,CO为△ABC的角平分线,连接OD,过O作OE⊥AB交BC于点E,交AD延长线于点F.
则下列四个结论,其中一定正确的是______.(填写正确序号)
①∠AOC=45°;
②;
③∠COD=∠B;
④BC-AC=AF.
第15题图
16.如图,在△ABC中,∠ACB=90°,∠B=50°,O是射线CB上的一个动点,连接OA,将△ACO沿着AO翻折得到△ADO,当△ADO的三边与△ABC的三边有一组边垂直时,则∠AOC=______°.
第16题图
三、解答题(共8小题,共72分)
下列各题需要在答题卷的指定位置写出文字说明、证明过程、演算步骤或画出图形.
17.(本题满分8分)如图,AD⊥BC,垂足为D,∠1=∠2,∠C=60°.求∠BAC的度数.
18.(本题满分8分)如图,AE⊥BC,DF⊥BC,垂足分别为E,F,且BF=CE,AE=DF.求证:AB∥CD.
19.(本题满分8分)如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠BAD=∠C+10°.求∠C的度数.
20.(本题满分8分)如图,在等边△ABC中,D为射线BA上一点,过D作DE∥BC交射线CA于点E,点F为AB边上一点,BF=DE,过F作FH⊥CE,垂足为点H.
(1)求证:DF=BC;
(2)求证:H为CE中点.
21.(本题满分8分)如图,是由边长为1的小正方形组成的15×9的网格,每个小正方形的顶点叫做格点.△ABC的三个顶点都是格点,AB=AC=10,仅用无刻度直尺在给定的网格中完成画图,画图的过程用虚线表示.
(1)在BC上画点D,使得AD平分△ABC的面积;
(2)在AB边上画点E,使得∠BCE=∠BAD;
(3)M为AC边上一点,在AB边上画点N,使得AN=AM;
(4)在平面内画点G,使得NG=2ND.
22.(本题满分10分)已知,在△ABC与△ADE中,AE=AC,AB=AD,∠BAC+∠DAE=180°.
(1)如图1,若AB=AC,AM⊥BC于点M.
①求证:∠E=∠BAM;
②猜想AM与DE之间的数量关系,并证明.
(2)如图2,求证:.
23.(本题满分10分)如图,O是△ABM内一点,OB=OM,,.
(1)已知,△ABC为等边三角形.
①如图1,若点C与点M重合,请补充条件:______°,可得结论:OA=OB=OM;
②如图2,若点C在边AM上,在①补充的条件下,结论OA=OB=OM是否仍成立?并说明理由;
(2)如图3,请探究当与之间满足什么数量关系时,结论OA=OB=OM仍然成立,并说明理由.
24.(本题满分12分)如图,在平面直角坐标系中,点A(a,0),点B(0,b),且a,b满足.
(1)直接写出△AOB的面积;
(2)如图1,若点C为线段OB上一点,连接AC,作CD⊥AC,且CD=AC,连接BD.求∠DBA的度数;
(3)如图2,在(2)的条件下,连接OD,点E,F分别为OD,AB的中点,连接CE,EF,请探究线段CE与EF之间的关系,并证明你的结论.
2024~2025学年度第一学期期中质量检测
八年级数学参考答案
一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确答案的标号填在下面的表格中.)
二、填空题(本大题共6个小题,每小题3分,共18分.把答案填在题中横线上.)
11.-6;12.4;13.AD=AE或∠B=∠C或∠AEB=∠ADC等;
14.80°或50°;15.①③④;16.70°或45°或25°.
三、解答题:(本大题共8个小题.共72分.解答应写出文字说明、证明过程或演算步骤.)
17.解:∵AD⊥BC ∴∠ADC=∠ADB=90°,∴∠1+∠2=90°,∠DAC+∠C=90°
∵∠1=∠2,∠C=60°,∴∠1=∠2=45°,∠DAC=90°-∠C=30°
∴∠BAC=∠1+∠DAC=45°+30°=75°.
注:本题其它解法参照评分.
18.证明:∵AE⊥BC,DF⊥BC,∴∠AEB=∠DFC=90°,
∵BF=CE ∴BF-EF=CE-BC 即:BE=CF
在△ABE和△DCF中 △ABE≌△DCF(SAS)
∴∠B=∠C ∴AB∥CD.
注:本题其它解法参照评分.
19.解:∵AB=AD=DC,∴设∠C=∠DAC=x° 则∠B=∠ADB=2x.
∵∠BAD=∠C+10° ∴∠BAD=(x+10)°
在△ABD中 ∠B+∠BAC+∠C=180° ∴x+10+2x+2x=180.
解得:x=34;∴∠C的度数为34°.
20.证明:(1)∵△ABC为等边△,∴AB=BC,∠B=∠C=∠BAC=60°
∵DE∥BC ∴∠B=∠D=60°,∠E=∠C=60°.
∴∠D=∠E=∠DAE=60°.∴△DAE为等边△.∴DE=AD.
∵BF=DE ∴AB=BF+AF=AD+AF=DF.∵AB=BC
∴DF=BC.
(2)连接EF,CF.
在△EDF和△FBC中 △EDF≌△FBC(SAS)
∴EF=CF.∵FH⊥CE,∴EH=HC.
即:H为CE中点.
注:本题两问其它解法参照评分.
21.(1)如图,点D即为所求;(2)如图,点E即为所求;
(3)如图,点N即为所求;(4)如图,点G即为所求.
注:本题几问其它画法参照评分.
22.(1)①证明:∵AE=AC,AB=AD,AB=AC,∴AE=AD
∴∠E=∠D ∴2∠E+∠DAE=180°
∵∠BAC+∠DAE=180°,∴∠BAC=2∠E.
∵AB=AC,AM⊥BC,∴∠BAC=2∠BAM.
∴∠E=∠BAM.
②猜想:.
证明:过A作AF⊥DE于F.
∵AE=AD ∴ ∵AM⊥BC ∴∠EFA=∠AMB=90°
在△EFA和△AMB中 △EFA≌△AMB(AAS)
∴.
(2)延长EA至G,使AE=AG,连接DG.
则∠EAD+∠DAG=180°,
∵∠BAC+∠DAE=180° ∴∠DAG=∠BAC
在△DAG和△BAC中 △DAG≌△BAC(SAS)
∴.
注:本题两问其它解法参照评分.
23.(1)①补充条件:,可得结论:OA=OB=OM;
②在①补充的条件下,结论OA=OB=OM成立,理由如下:
证明:连接OC,在BC上截取BD=CM,连接OD.
∵△ABC为等边三角形 ∴AB=AC=BC,∠ACB=60°.
∴∠BCM=180°-∠ACM=120°=∠BOM.
又∵∠BOM+∠OBC=∠BCM+∠CMO=∠1 ∴∠OBC=∠OMC.
在△OBD和△OMC中 ∴△OBD≌△OMC(SAS)
∴OD=OC,∠BOD=∠MOC.
∴∠DOC=∠DOM+∠MOC=∠DOM+∠BOD=∠BOM=120°.
∴∠OCD=∠ODC=30°.又∵∠ACB=60°
∴∠AOC=∠ACB-∠OCD=30°.
在△AOC和△BOC中 ∴△AOC≌△BOC(SAS)
∴OA=OB.又∵OB=OM
∴OA=OB=OM.
(2)解:当时,①中结论OA=OB=OM成立
证明:在AM上找一点C,使
在BC上截取BD=CM,连接OD.
又∵∠BOM+∠OBC=∠BCM+∠CMO=∠1 ∴∠OBC=∠CMO.
在△OBD和△OMC中 ∴△OBD≌△OMC(SAS)
∴OD=OC.
∠BOD=∠MOC ∴
∴
∵ ∴
∴ ∴∠ACO=∠BCO
∵,
∴ ∴∠ABC=∠BAC ∴AC=CB
在△ACO和△BCO中 ∴△ACO≌△BCO(SAS)
∴AO=OB 又∵OB=OM ∴AO=OB=OM.
注:本题几问其它解法参照评分.
24.(1)△AOB的面积为8.
(2)作DH⊥y轴于H,
∵CD⊥AC,∴∠DHC=∠COA=∠DCA=90°.
∴∠DCH+∠OCA=∠OCA+∠OAC=90°.
∴∠DCH=∠CAO.
在△DHC和△COA中 ∴△DHC≌△COA(AAS)
∴DH=OC,CH=OA=OB=4.∴BH+BC=BC+OC.
∴BH=OC=DH.∴∠HBD=∠HDB=45°.
∵OA=OB,∠AOB=90° ∴∠OBA=∠OAB=45°.
∴∠DBA=90°.
(3)连接OF,延长FE交BD于G,连接CG,CF.
∵OB=OA,F为AB中点,∴OF⊥AB.∴∠OFB=∠DBA=90°.
∴DB∥OF.∴∠BDE=∠FOE.∵E为OD中点,∴ED=EO,
在△DEG和△OEF中 ∵ ∴△DEG≌△OEF(ASA)
∴DG=OF,EG=EF.
∵∠DHA=∠DBA+∠BDH=∠DCA+∠CAH,∠DBA=∠DCA=90°
∴∠BDH=∠CAF.
在△GDC和△FAC中 ∵ ∴△GDC≌△FAC(SAS)
∴GC=CF,∠GCD=∠FCA.∴∠GCF=∠DCA=90°.
∴△GCF为等腰直角三角形.
∵EG=EF ∴CE⊥EF,CE=EF.
注:本题两问其它解法参照评分.
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
D
C
C
C
B
B
A
相关试卷
这是一份湖北省武汉市青山区2024-2025学年八年级上学期期中数学试题,文件包含湖北省武汉市青山区2024-2025学年八年级上学期11月期中数学试题pdf、八上期中答案pdf等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
这是一份2020-2021学年湖北省武汉市青山区八年级下学期期中数学试题及答案,共26页。
这是一份湖北省武汉市青山区2023-2024学年八年级下学期期中数学试题,共29页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









