
江西省赣州市于都县2024-2025学年 上学期九年级数学期中试卷(无答案)
展开
这是一份江西省赣州市于都县2024-2025学年 上学期九年级数学期中试卷(无答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
(考试时间为120分钟,满分为120分)
一、选择题(本大题共6小题,每小题3分,共18分)
1.《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来,下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )
A.B.C.D.
2.若关于x的一元二次方程有一个根为0,则a的值为( )
A.B.1C.D.0
3.用配方法解一元二次方程,下列变形正确的是( )
A.B.C.D.
4.如图,将绕着点O逆时针旋转至,使点B恰好落在线段上,若,则的度数为( )
A.B.C.D.
5.关于二次函数;下列叙述正确的是( )
A.函数的图象开口向下B.对称轴是y轴
C.当时,y有最大值D.当时,y随x的增大而增大
6.生物学研究表明、在一定的温度范围内,酶的活性会随温度的升高逐渐增强,在最适宜温度时,酶的活性最强,超过一定温度范围时,酶的活性又随温度的升高逐渐减弱,甚至会失去活性.现已知某种酶的活性值y(单位:IU)与温度t(单位:℃)的关系可以近似用二次函数来表示.则当温度为最适宜时,该种酶的活性值为( )
A.14B.C.240D.44
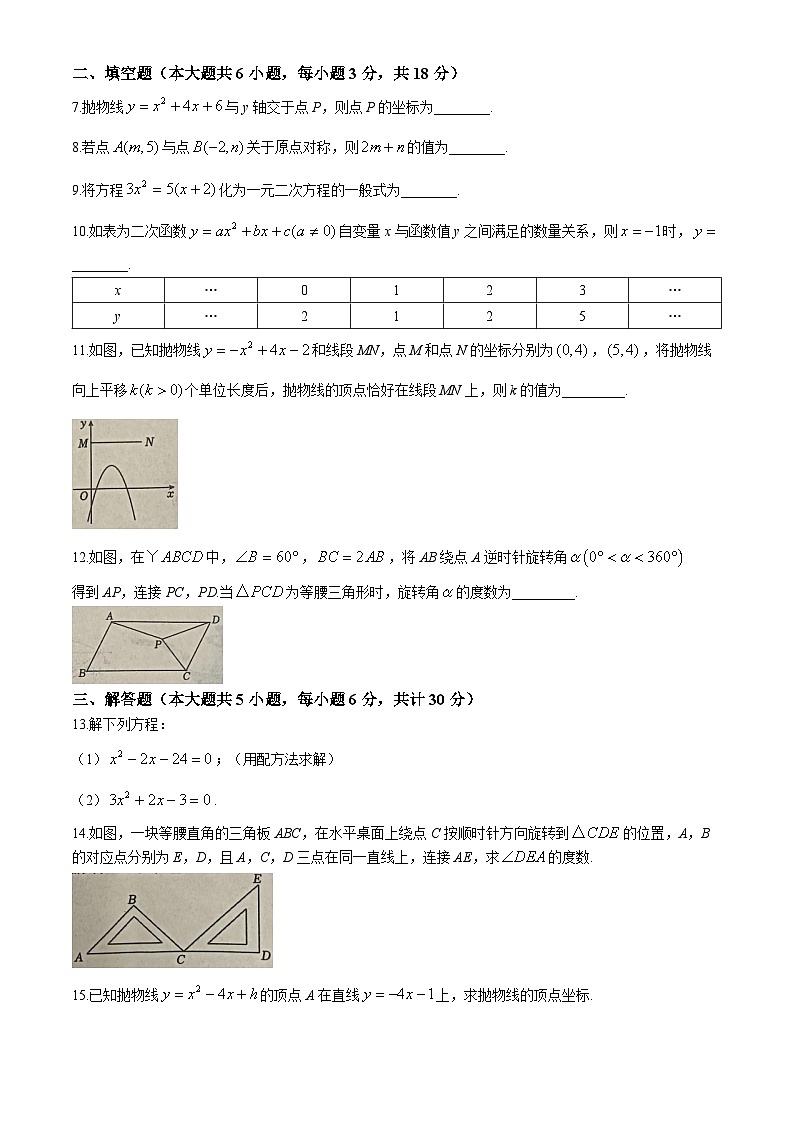
二、填空题(本大题共6小题,每小题3分,共18分)
7.抛物线与y轴交于点P,则点P的坐标为________.
8.若点与点关于原点对称,则的值为________.
9.将方程化为一元二次方程的一般式为________.
10.如表为二次函数自变量x与函数值y之间满足的数量关系,则时,________.
11.如图,已知拋物线和线段MN,点M和点N的坐标分别为,,将抛物线向上平移个单位长度后,抛物线的顶点恰好在线段MN上,则k的值为_________.
12.如图,在中,,,将AB绕点A逆时针旋转角
得到AP,连接PC,PD.当为等腰三角形时,旋转角的度数为_________.
三、解答题(本大题共5小题,每小题6分,共计30分)
13.解下列方程:
(1);(用配方法求解)
(2).
14.如图,一块等腰直角的三角板ABC,在水平桌面上绕点C按顺时针方向旋转到的位置,A,B的对应点分别为E,D,且A,C,D三点在同一直线上,连接AE,求的度数.
15.已知抛物线的顶点A在直线上,求抛物线的顶点坐标.
16.若点关于原点对称的点是第一象限的点,求a的取值范围.
17.图1、图2均为的正方形网格,每个小正方形的顶点称为格点,的顶点和点D均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求作图、并保留作图痕迹.
图1图2
(1)在图1中,画出将绕点D顺时针旋转得到的;
(2)在图2中,画出,使与关于点D成中心对称.
四、解答题(本大题共3小题,每小题8分,共24分)
18.如图是一张长12dm,宽6dm的长方形纸板,将纸板四个角各剪去一个同样的边长为x dm的正方形,然后将四周突出部分折起,可制成一个无盖长方体纸盒.
(1)无盖方盒盒底的长为_________dm,宽为_________dm(用含x的式子表示).
(2)若要制作一个底面积是的一个无盖长方体纸盒,求剪去的正方形边长x.
19.若二次函数的x与y的部分对应值如表:
(1)求此二次函数的解析式;
(2)画出此函数图象.
20.已知关于x的一元二次方程.
(1)求证:该方程总有两个实数根;
(2)若该方程有一个根小于2,求k的取值范围.
五、解答题(本大题共2小题,每小题9分,共计18分)
21.阅读与思考
下面是小文撰写的数学小论文,请仔细阅读并完成相应任务.
任务:
(1)已知p,q是两个常数,一元二次方程的两个实数根为,,则二次三项式分解因式的结果是________.
(2)因式分解:的结果是________.
(3)请用阅读内容中的方法,因式分解:.
22.我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两段抛物线组合而成封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示,如果把锅纵断面的抛物线记为,把锅盖纵断面的抛物线记为.
实物图图①
(1)求和的解析式;
(2)如果炒菜时锅的水位高度是1dm,求此时水面的直径;
(3)如果将一个底面直径为3dm,高度为3.2dm的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
六、解答题(本大题共12分)
23.通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.
原题:如图1,点E、F分别在正方形ABCD的边BC,CD上,,连接EF,试猜想EF,BE,DF之间的数量关系.
图1图2图3
(1)思路梳理:把绕点A逆时针旋转至,可使AB与AD重合,由,得,即点F,D,G共线,易证_________,故EF,BE,DF之间的数量关系为________.
(2)类比引申:如图2,点E,F分别在正方形ABCD的边CB,DC的延长线上,.连接EF,试猜想EF,BE,DF之间的数量关系为__________,并给出证明.
(3)联想拓展:如图3,在中,已知,垂足于点D,且,.求AD的长.x
…
0
1
2
3
…
y
…
2
1
2
5
…
x
…
0
1
…
y
…
0
3
4
3
0
…
通过解一元二次方程分解某些二次三项式我们把形如(a,b,c是常数,)的多项式叫做关于x的二次三项式.通过初中学习可知,利用因式分解可解某些一元二次方程.反过来,是否可以利用求出一元二次方程两个根的方法,把某些二次三项式分解因式呢?根据下面代数推理,可以得出结果,设一元二次方程的两个实数根为,,直接计算:.下面是代数推理过程:
解:
.
即.
这就是说,在因式分解二次三项式时,可先求一元二次方程的两个实数根,然后写成.即通过解一元二次方程可以将某些二次三项式分解因式.
相关试卷
这是一份江西省赣州市于都县丰田初级中学 2024-2025学年九年级上学期10月月考数学试题(无答案),共4页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。
这是一份江西省赣州市于都县丰田初级中学 2024-2025学年九年级上学期10月月考数学试题,共6页。
这是一份江西省赣州市于都县2023-2024学年七年级下学期期末数学试题(无答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








