2023-2024学年高二数学下学期期末考试模拟03

这是一份2023-2024学年高二数学下学期期末考试模拟03，文件包含2023-2024学年高二数学下学期期末考试模拟03教师版docx、2023-2024学年高二数学下学期期末考试模拟03学生版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
1. 在等差数列中，，则的值是（ ）
A. 12B. 18C. 24D. 30
【答案】D
【解析】
【分析】利用等差数列的性质计算即可.
【详解】由题意可知：.
故选:D
2. 若随机变量服从两点分布，其中，分别为随机变量的均值与方差，则下列结论不正确的是（ ）
A B.
C. D.
【答案】C
【解析】
【分析】根据随机变量服从两点分布推出，根据公式先计算出、，由此分别计算四个选项得出结果.
【详解】随机变量服从两点分布，其中，，
，
，
在A中，，故A正确；
在B中，，故B正确；
在C中，，故C错误；
D中，，故D正确.
故选：C
3. 离散型随机变量X的分布列中部分数据丢失，丢失数据以x，代替，分布列如下：则 （ ）
A. 0.35B. 0.45C. 0.55D. 0.65
【答案】B
【解析】
【分析】根据概率之和为1得到方程组，求出，得到答案.
【详解】由题意得，解得，
，解得，
故.
故选：B
4. 元宵节是中国传统节日，当天人们会吃汤圆、赏花灯、猜灯谜.小华爸爸手里有6个灯谜，其中4个事物谜，2个字谜，小华随机抽取2个灯谜，事件A为“取到的2个为同一类灯谜”，事件B为“取到的2个为事物谜”，则（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据题意，由条件概率公式代入计算，即可得到结果.
【详解】由题意可得，，，
所以，
故选：B.
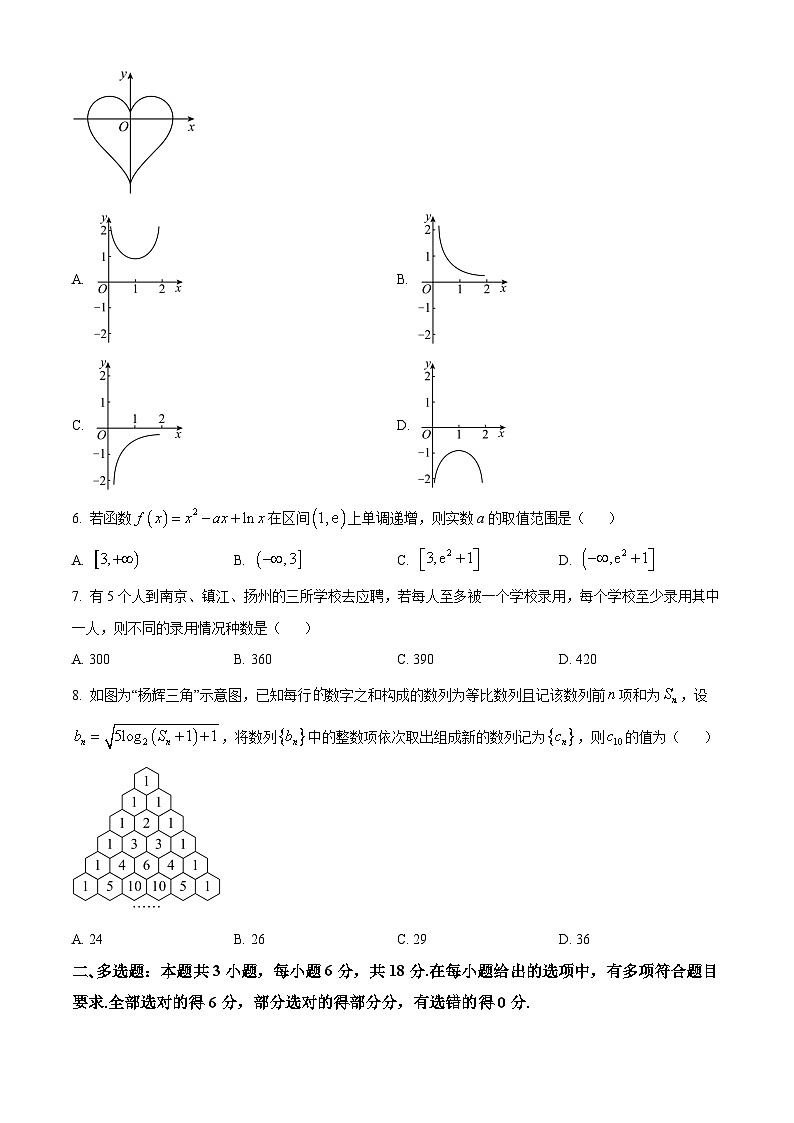
5. 某同学利用电脑软件将函数，的图象画在同一直角坐标系中，得到如图的“心形线”.观察图形，当时，的导函数的图象大致为（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】根据导数的几何意义判断即可.
【详解】，，
所以轴下方的图象为函数的图象，
当时，函数单调递增，所以，故排除CD；
根据导数的几何意义可知，时，函数图象上每点处的切线斜率应先变小，再增大，故排除B，只有A正确.
故选：A
6. 若函数在区间上单调递增，则实数a的取值范围是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据函数的单调性与导函数之间的关系，将单调性转化为导函数恒大于或等于0，即可求解.
【详解】依题意在区间上恒成立，即在区间上恒成立.
令，则，所以在上单调递增，则，所以.
故选:B.
7. 有5个人到南京、镇江、扬州的三所学校去应聘，若每人至多被一个学校录用，每个学校至少录用其中一人，则不同的录用情况种数是（ ）
A. 300B. 360C. 390D. 420
【答案】C
【解析】
【分析】由排列、组合及简单计数问题，结合分类加法计数原理及平均分组问题求解.
【详解】(1)当5人中有三人被录取，则不同的录取情况数为;
(2)当5人中有四人被录取，则不同的录取情况数为；
(3)当5人全部被录取，则不同的录取情况数为；
综上不同的录取情况数共有.
故选：C
8. 如图为“杨辉三角”示意图，已知每行的数字之和构成的数列为等比数列且记该数列前项和为，设，将数列中的整数项依次取出组成新的数列记为，则的值为（ ）

A. 24B. 26C. 29D. 36
【答案】B
【解析】
【分析】根据已知等比数列求得其前项和，代入，整理得到，要求中的整数项，需使的最末位是1或6，列出数列的相关项，即得的值.
【详解】依题意，题中的等比数列为，故该数列前项和，则，
要使数列中只取得整数项，需使是5的正整倍数即可，即使的最末位是1或6即可，
于是新的数列的项依次为：4，6，9，11，14，16，19，21，24，26，29，31，，
故
故选：B.
二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9. 为数列的前n项和，已知对任意的，，下列说法正确的是（ ）
A. B. C. D.
【答案】AC
【解析】
【分析】根据给定的递推公式，结合前n项和的意义计算判断AC；分析判断BD.
【详解】数列中，对任意的，，
，，AC正确；
由，知的值无法确定，则通项也无法确定，BD错误.
故选：AC
10. 已知的展开式中第4项与第7项的二项式系数相等，且各项系数的和为0，则（ ）
A.
B. 的展开式中的有理项有5项
C. 的展开式中偶数项的二项式系数之和为512
D. 除以9的余数为8
【答案】BD
【解析】
【分析】由二项式系数的概念和组合数的性质可判断选项A；结合有理项的概念，根据二项式的通项可判断选项B；由偶数项的二项式系数和可判断选项C；结合二项式定理可判断选项D.
【详解】由的展开式中第4项与第7项的二项式系数相等可得：，
由组合数的对称性可得：，故选项A错误；
因为的展开式中各项系数的和为0，
所以令可得：，解得：.
则的二项式通项为.
由为整数可得：，
所以的展开式中的有理项有5项，故选项B正确；
因为展开式中偶数项的二项式系数之和为，故选项C错误；
因为
所以除以9的余数为8，故选项D正确.
故选：BD.
11. 关于函数，下列判断正确的是（ ）．
A. 是的极大值点
B. 函数有且只有1个零点
C. 存在正实数，使得成立
D. 对任意两个正实数，且，若，则．
【答案】BD
【解析】
【分析】求导后讨论单调性可判断A；求导后讨论的单调性，利用零点存在定理判断B；利用常数分离法，构造函数，利用导数分析得的单调性可判断C；利用极值点偏移问题的解法求解，从而可判断D.
【详解】对于选项A，函数的定义域为，函数的导数，
所以在内，，函数单调递减；
在上，，函数单调递增，
所以是的极小值点，故A错误；
对于选项B，由，得，
由于分子判别式小于零，所以恒成立，
所以函数在，上单调递减，
且，
所以函数有且只有1个零点，故B正确；
对于选项C，若，可得，
令，则，
令，则，
所以在内，，函数单调递增；
在上，，函数单调递减，
所以，所以，
所以函数在上单调递减．
又因为当时，，
所以不存在正实数，使得恒成立，故C不正确；
对于选项D，设，即有，
，即为，
化为，
故，所以，
则，
设（），可得，
令，则在上恒成立，
可得，所以，故单调递增，
可得，故成立，故D正确．
故选：BD.
【点睛】方法点睛：
（1）函数的极值点与零点可用导数分析单调性后再结合具体函数值分析；
（2）对于含参数的函数不等式恒成立问题可分离参数后求导，分析单调性再求参数的范围；
（3）极值点平移问题，先构造函数求导，再赋值，最后可得
三､填空题：本题共3小题，每小题5分，共15分.
12. 某座山，若从东侧通往山顶的道路有3条，从西侧通往山顶的道路有2条，那么游客从上山到下山共有______种不同的走法
【答案】25
【解析】
【分析】根据给定条件，利用分步乘法计数原理计算作答.
【详解】依题意，游客上山有5种方法，下山有5种方法，由分步计数乘法原理知，从上山到下山方法共有种，
所以游客从上山到下山共有25种不同的走法.
故答案为：25
13. 某公司定期对流水线上的产品进行质量检测，以此来判定产品是否合格可用．已知某批产品的质量指标服从正态分布，其中的产品为“可用产品”，则在这批产品中任取1件，抽到“可用产品”的概率约为________．
参考数据：若，则，，．
【答案】0.84##
【解析】
【分析】由正态分布的性质可知，有，结合原则即可求解.
【详解】由题意知，该产品服从，则，
所以
，
又，
，
所以，
所以，
即.
所以抽到“可用产品”的概率为.
故答案为：0.84.
14. 若曲线有两条过点的切线，则的取值范围是______.
【答案】
【解析】
【分析】先利用导数求曲线过坐标的切线方程，再列出关于的不等式，进而求得的取值范围.
【详解】由得，设切点坐标，
则切线斜率，
切线方程为，
又因为切线过，所以，整理得，
又曲线有两条过坐标原点的切线，所以该方程有两个实数解，
所以，解得或，
所以的取值范围是，
故答案为：.
四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.
15. 已如曲线在处的切线与直线垂直.
（1）求的值；
（2）若恒成立，求的取值范围.
【答案】（1）
（2）
【解析】
【分析】（1）根据斜率关系，即可求导求解，
（2）求导判断函数的单调性，即可求解函数的最值求解.
【小问1详解】
由于的斜率为，所以，
又,故，解得，
【小问2详解】
由（1）知，所以，
故当时，单调递增，
当时，单调递减，
故当时，取最小值，
要使恒成立，故，解得，
故的取值范围为
16. 在某诗词大会的“个人追逐赛”环节中，参赛选手应从8个不同的题目中随机抽取3个题目进行作答．已知这8个题目中，选手甲只能正确作答其中的6个，而选手乙正确作答每个题目的概率均为0.8，且甲、乙两位选手对每个题目作答都是相互独立的．
（1）求选手甲恰好正确作答2个题目的概率；
（2）记选手乙正确作答的题目个数为X，求X的分布列和数学期望；
（3）如果在抽取的3个题目中答对2个题目就可以晋级，你认为甲、乙两位选手谁晋级的可能性更大？请说明理由．
【答案】（1）
（2）分布列见解析，
（3）选手乙，理由见解析
【解析】
【分析】（1）由题意选手甲需要从能正确作答其中的6个的题目中正确作答2个题目，在剩余的2个不会的题目中答1个，再求解概率即可；
（2）由题意得，，再根据二项分布的性质求解分布列与数学期望即可；
（3）分别计算甲乙两人答对2或3个题目的数学概率进行判断即可.
【小问1详解】
设事件A为“选手甲正确作答2个题目”，则．
故选手甲恰好正确作答2个题目的概率为．
【小问2详解】
由题意得，，X的所有可能取值为0，1，2，3，
∴，，，，
∴X的分布列为
∴．
【小问3详解】
设选手甲正确作答的题目个数为Y，则Y的所有可能取值为0，1，2，3，
∴，，
∴．
∵，
∴，
∴可以认为选手乙晋级的可能性更大．
17. 在公差不为0的等差数列中，，且成等比数列．
（1）求的通项公式；
（2）若，求数列的前项和．
【答案】（1）
（2）
【解析】
【分析】（1）根据等差数列的性质、通项公式和等比中项的应用建立关于d的方程，解之即可求解；
（2）由（1）可得，结合裂项相消求和法即可求解.
【小问1详解】
设的公差为d（），
由，得，即．
由成等比数列可得，
即，
解得或（舍去），
所以，故．
【小问2详解】
由（1）得，
所以．
18. 有甲、乙两个不透明的罐子，甲罐有3个红球，2个黑球，球除颜色外大小完全相同．某人做摸球答题游戏．规则如下：每次答题前先从甲罐内随机摸出一球，然后答题．若答题正确，则将该球放入乙罐；若答题错误，则将该球放回甲罐．此人答对每一道题目的概率均为．当甲罐内无球时，游戏停止．假设开始时乙罐无球．
（1）求此人三次答题后，乙罐内恰有红球、黑球各1个的概率；
（2）设第次答题后游戏停止的概率为．
①求；
②是否存在最大值？若存在，求出最大值；若不存在，试说明理由．
【答案】（1）
（2）①，②存在，最大值
【解析】
【分析】（1）根据全概率公式即可求解，
（2）根据题意可得，即可利用作商求解单调性，即可求解最值.
【小问1详解】
记“此人三次答题后，乙罐内恰有红、黑各一个球”，
“第次摸出红球，并且答题正确”，；
“第次摸出黑球，并且答题正确”，；
“第次摸出红球或黑球，并且答题错误”，，
所以．
又；；，
所以
．
同理：
所以．
【小问2详解】
①第次后游戏停止的情况是：前次答题正确恰好为4次，答题错误次，且第次摸出最后一球时答题正确．
所以．
②由①知，
所以．
令，解得；，解得．
所以，
所以的最大值是．
19. 已知函数，其中．
（1）当时，求的极值；
（2）讨论当时函数的单调性；
（3）若函数有两个不同的零点、，求实数a的取值范围.
【答案】（1）的极大值为，无极小值.
（2）答案见解析 （3）．
【解析】
【分析】（1）求出函数的定义域与导函数，即可得到函数的单调区间，从而求出函数的极值；
（2）求出函数的导函数，再分、、三种情况讨论，分别求出函数的单调区间；
（3）由函数有两个不同的零点、，构造函数利用导数研究函数单调性的最值，结合函数图像求实数的取值范围；
【小问1详解】
当时，的定义域为，

当时，，当时，
在上单调递增，在上单调递减.
处取得极大值，
的极大值为，无极小值.
【小问2详解】
函数的定义域为，
又．
当时，令则或．
①当，即时，当时，；当时，，
在上单调递增，在上单调递减.
②当，即时，在上恒成立，在上单调递增.
③当，即时，当时，；当时，，
在上单调递增，在上单调递减.
综上，当时，在上单调递增，在上单调递减；
当时，在上单调递增；
当时，在上单调递增，在上单调递减
【小问3详解】
有两个不同的零点、，
即有两个不同正实根，得有两个不同正实根，
即与有两个交点，
令，则，令，得，
当时，，在上单调递增，
当时，，在上单调递减，
时，取得最大值，且，当时，
得的大致图像如图所示：

，解得，所以实数的取值范围为．
1
2
3
4
5
6
0.21
0.20
0.10
0.10
X
0
1
2
3
P
0.008
0.096
0.384
0.512