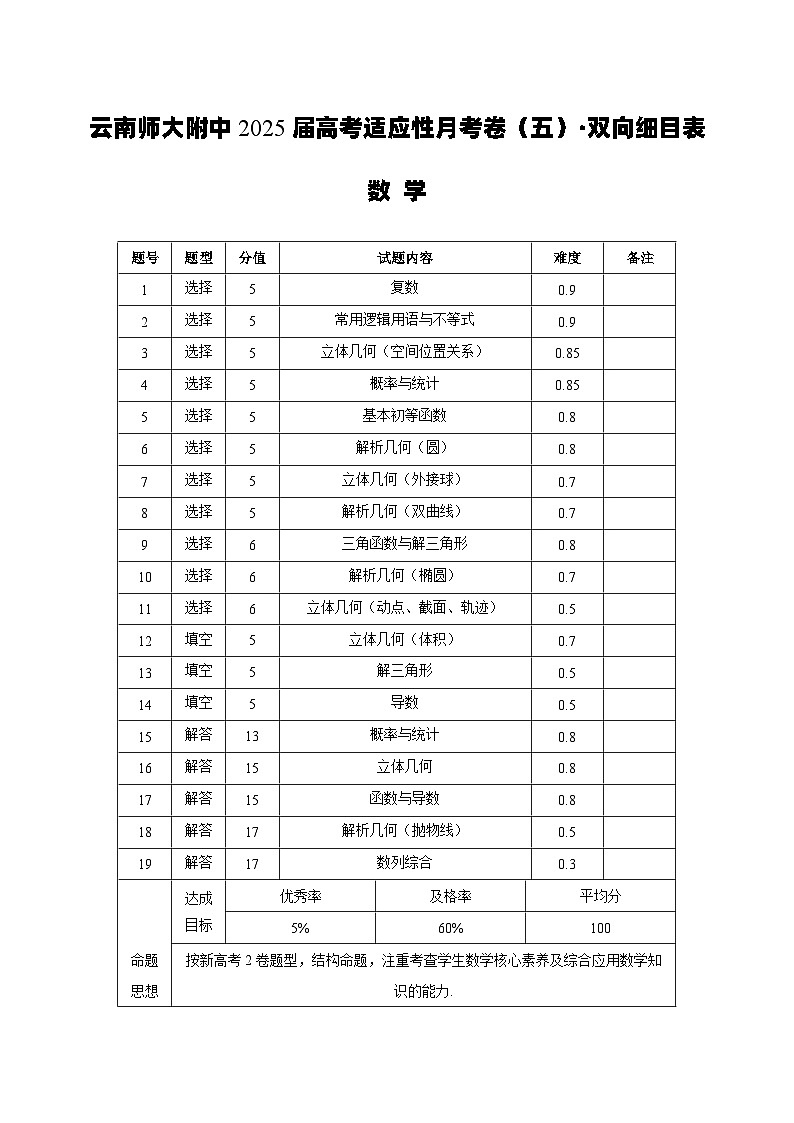
云南省云南师范大学附属中学2024-2025学年高三上学期高考适应性月考卷（五）数学

这是一份云南省云南师范大学附属中学2024-2025学年高三上学期高考适应性月考卷（五）数学，文件包含云南省云南师范大学附属中学2024-2025学年高考适应性月考卷五数学答案docx、云南省云南师范大学附属中学2024-2025学年高考适应性月考卷五数学pdf、云南省云南师范大学附属中学2024-2025学年高考适应性月考卷五数学双向细目表docx等3份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
【解析】
1．因为所以，故选D．
2．因为，，所以，充分性成立；若，则，必要性不成立，故选A．
3． A选项，直线在同一平面才能推出，故A错误；B选项，若为一底面为的圆锥的两条母线，则与所成角相同，此时相交，故B错误；D选项，若，则平行或异面，故D错误；C选项，在平面中分别存在直线（异于），使得，则，可推出，从而得到，故，故选C．
4．用水在10.2t以下的居民用户所占比例为，故．由得，故选A．
5．是偶函数且在上单调递增，所以，而，所以；，所以，故选B．
6．因为直线分别过点，且两直线垂直，所以点的轨迹为圆心在，半径的圆(除去点)．因为，所以最大值为，故选B．
7．取中点，的三等分点（靠近），则，分别为平面，平面与球截面圆的圆心．由可得，再由余弦定理得，所以，在中可得，故，所以球的表面积为，故选C．
8．设右焦点坐标为，因为所以所以．在直角中，由直线可得，所以，又因为，所以．在中，，设，则，又，解得，所以，，故，故选C．
二、多项选择题（本大题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分）
【解析】
9．由五点作图法知，，解得，于是，故选项A正确；由于，，故选项B错误；的图象关于点对称，故点也在的图象上，故选项C正确；的图象关于对称，故点在的图象上，故选项D正确，故选ACD．
10．设，则，化简得：，所以点的轨迹为以为焦点的椭圆，，A错误；当P为短轴端点时，面积取到最大为：，B正确；若，点在以AB为直径的圆上，因为该圆在椭圆：内部，所以这样的点不存在，C错误；作，则，，即当点为右顶点时，取到最小值4，D正确，故选BD．
图2
图1
11．由，其中可知，点在底面上，当，在上，且，如图1，平面截正方体所得截面为五边形，所以A错误；当时，，点与点C重合，在正方体中，平面，所以此时平面，所以B正确；当时，点上，将等边三角形向下翻折到正方形ABCD所在的平面，当共线时，取得最小值为，所以C正确；当时，以点为球心，半径为作球，该球与底面的截面圆如图2，P的轨迹为，，，，，所以动点的轨迹长度为，D错误，故选BC．
三、填空题（本大题共3小题，每小题5分，共15分）
【解析】
12．因为圆锥的底面积为，所以底面圆半径为1，又因为，所以母线长为，求得圆锥的高，所以体积．
13．因为，所以，又，故，解方程组得，．
14．，．设两极值点为，其中.则： ，且，，解得：，此时极小值为由于，所以，故
．令，则，所以在上单调递减．由知，于是，从而．故第一空为，第二空为．
四、解答题（本大题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤）
15．（本小题满分13分）
解：（1）的所有可能取值为0，1，2，其中
，
，
，
所以的分布列为
………………………………（5分）
．………………………………（8分）
（2）记A=“2个球来自甲袋”，=“2个球来自乙袋”，=“摸到1个红球1个白球”，
则，
，
故所求为．………………………………（13分）
16．（本小题满分15分）
（1）证明：取的中点，连接，
由题可知，所以，………………………………（2分）
因为，所以，
又因为，所以，
所以，，
所以，.………………………………（4分）
又，所以，
又因为，所以．
……………………………………………（6分）
（2）解：以M为原点，MA为x轴，MB为y轴，平行于PG
的直线为z轴，建立如图3所示坐标系．
，
图3
，
………………………………………（9分）
设平面法向量为，
则令，得，
…………………………………………………（11分）
因为平面的一个法向量为，………………………………（13分）
设平面和平面夹角为，
所以．………………………………………………………（15分）
17．（本小题满分15分）
解：（1）由题得，
设切点为，则，解得或．
………………………………（2分）
当时，，解得；………………………………（3分）
当时，，
令，则，
故在上单调递增，在上单调递减，
所以，于是无解．
综上，．………………………………（5分）
（2）由（1）对参数作如下讨论：
若，
则当时，，单调递增；当时，，单调递减，所以，不合题意；………………………………（7分）
若，
则当时，，单调递减；当时，，单调递增；当时，，单调递减．
所以，
由于，只需，解得；
………………………………（9分）
若，
则当时，，单调递减，
所以，符合题意；
………………………………………………………………（11分）
若，
则当时，，单调递减；
当时，，单调递增；当时，，单调递减，
所以，
由于，只需，
由（1）知，当，故符合题意；
………………………………………………（13分）
若，
则当时，，单调递减；当时，，单调递增，
所以，
由于，，故符合题意．
综上可得，的取值范围为．…………………………………………（15分）
18．（本小题满分17分）
（1）解：因为F为抛物线的焦点，所以，
因为，所以，
又因为的面积为2，所以，解得，
所以抛物线E的方程为．………………………………（5分）
（2）①证明：设，
联立得，，
联立得，，
………………………………………………（7分）
，代入，
化简得：①，
同理得：②，……………………………………………（9分）
联立①②可得：
，
所以H在定直线上；………………………………（11分）
②解：将H坐标分别代入①②，
可得：，因为，
所以，，
代入，得，解得，
………………………………………………（14分）
所以的面积为．
……………………………………（17分）
19．（本小题满分17分）
（1）解：由题得，
若，则令，得，即；……………………（1分）
当时，，，即，
故是首项为、公比为2的等比数列．……………………（4分）
所以．……………………（5分）
若，则令，得，即；
当时，，，即，
故是首项为、公比为的等比数列．
所以．
注：本小问答案不唯一，除了上述两个还有其它符合题意的数列，可酌情给分．
（2）证明：由题得，
当时，，解得，结论成立；
当时，，即，
利用求根公式得．……………………（7分）
而，所以．
所以．
综上，．……………………（10分）
（3）解：假设存在等差数列是“数列”，
设，
则，
代入得，．
若，则，此时，，，即；
……………………………（12分）
若，则，，即，
比较等式两边的次数可知，，即．
此时，
所以，．
所以，．
此时．
综上，当，，时，；当，时，；
其余情形不存在．………………………………（15分）
当存在时，
①若，，则的最小值为；
②若，则由得，当且仅当时取等．
而
，
所以当，即时，取到最小值．
综上，最小值为，此时．……………………（17分）题号
1
2
3
4
5
6
7
8
答案
D
A
C
A
B
B
C
C
题号
9
10
11
答案
ACD
BD
BC
题号
12
13
14
答案
0
1
2