- 北师大版2024-2025学年七年级数学上册同步讲义第3章第04讲解题技巧专题:整式中化简求值与含字母参数的问题(学生版+解析) 学案 0 次下载
- 北师大版2024-2025学年七年级数学上册同步讲义第3章第05讲探究与表达规律(学生版+解析) 学案 0 次下载
- 北师大版2024-2025学年七年级数学上册同步讲义第4章第02讲比较线段的长短(学生版+解析) 学案 0 次下载
- 北师大版2024-2025学年七年级数学上册同步讲义第4章第03讲角(学生版+解析) 学案 0 次下载
- 北师大版2024-2025学年七年级数学上册同步讲义第4章第04讲思想方法专题:线段与角计算中的思想方法(学生版+解析) 学案 0 次下载
北师大版2024-2025学年七年级数学上册同步讲义第4章第01讲线段、射线、直线(学生版+解析)
展开知识点01 线段、射线、直线的概念
1.线段的表示也有两种:一个小写字母或用端点的两个大写字母.但前面必须加“线段”两字,如:线段a;线段AB.
2.射线的表示同样有两种:一个小写字母或端点的大写字母和射线上的要给大写字母,前面必须加“射线”两字
3.直线的表示有两种:一个小写字母或两个大写字母.但前面必须加“直线”两字,如:直线;直线m,直线AB;直线CD
基本概念:
【即学即练1】
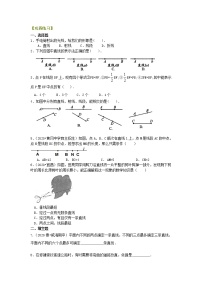
1.(23-24六年级下·全国·假期作业)如图,表示方法正确的是( )
A.①②B.②④C.③④D.①④
2.(23-24六年级下·山东烟台·期中)在日常生活中,手电筒发射出来的光线,类似于 .(填“折线”或“线段”或“射线”或“直线”)
3.(23-24六年级下·全国·假期作业)根据如图所示的图形填空:
(1)点B在直线_________,点C在直线_________;
(2)点E是直线与_________直线_________的交点,直线与直线相交于点_________;
(3)过点A的直线有_________条,分别是__________________.
知识点02 直线的性质
经过两点有一条直线,并且只有一条直线.简单地:两点确定一条直线. 两条直线相交,只有一个交点.
【即学即练2】
1.(23-24七年级上·贵州贵阳·期末)墨斗被认为是“百作手艺祖师爷”鲁班的发明,是木匠用来弹、放各种线记的重要工具,以其“绳之以墨”的功能成为了文人墨客心中正直的化身.如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 .
题型01 直线、射线、线段的联系与区别
【典例1】(2024·河北邢台·三模)下列图形中,可以表示为“线段”的是( )
A.B.
C.D.
【变式1】(23-24六年级下·全国·假期作业)图中直线的表示方法,不正确的有( )
A.1个B.2个C.3个D.4个
【变式2】(23-24七年级上·河南平顶山·期末)如图,对于图中直线的描述,正确的是( )
A.图中有直线B.图中有直线
C.直线与直线交于点OD.直线与直线m交于点O
【变式3】(23-24七年级上·全国·单元测试)小明根据下列语句,分别画出了图形,并将图形的标号填在了相应的“语句”后面的横线上.其中正确的是( )
①直线经过点三点,并且点在点与之间;
②点在线段的反向延长线上;
③点是直线外一点,过点的直线与直线相交于点;
④直线相交于点.
A.①②③④B.①②④C.①③④D.②③
题型02 点与线的位置关系
【典例2】(23-24七年级上·河北唐山·期末)平面上有A,B,C三点,如果,,,那么下列说法正确的是( )
A.点C在线段上B.点C在线段的延长线上
C.点C在直线外D.点C的位置无法确定
【变式1】(23-24七年级上·吉林·期末)如图,直线m和直线n相交于点O,对于图形,说法正确的语句有( )
①点O在直线m上.
②点O在直线n上.
③点O在直线m上. 也在直线n上.
④直线m经过点O.
A.1个.B.2个.C.3个.D.4个.
【变式2】(23-24七年级上·河北石家庄·阶段练习)下列几何图形与相应语言描述不相符的是( )
A.如图甲所示,直线不经过点P
B.如图乙所示,直线a与直线b交于点O
C.如图丙所示,点C在线段上
D.如图丁所示,线段与射线一定相交
【变式3】(2023七年级上·江苏·专题练习)如图,用适当的语句表述图中点与直线的关系,错误的是( )
A.点P在直线外B.点C在直线外
C.直线不经过点MD.直线经过点B
题型03 两点确定一条直线
【典例3】(23-24六年级下·山东东营·开学考试)要在墙壁上固定一根小木条,至少需要两枚钉子,其数学原理是 .
【变式1】(23-24七年级上·河南新乡·期末)如图,木匠师傅经过刨平的木板上的A,B两点,可以弹出一条笔直的墨线,请你解释这一实际应用的数学基本事实是 .
【变式2】(23-24六年级下·山东青岛·阶段练习)要种一列排列笔直的树,小明说:只要先定下两棵树的位置,然后其他树的位置就容易确定了,你认为小明这样说根据的数学原理是 .
【变式3】(23-24七年级上·福建厦门·期末)暑假期间,小华参加了夏令营打靶瞄准训练,如图所示,打靶瞄准用到的数学原理是 .
题型04 直线、线段、射线的数量问题
【典例4】(23-24七年级上·河南郑州·期末)如图,小金同学根据图形写出了三个结论:①图中共有6条线段;②图中共有1条直线;③图中射线与射线不是同一条射线.其中结论正确的是( )
A.①②B.①③C.②③D.①②③
【变式1】(23-24七年级上·四川成都·开学考试)图中,共有 条线段.
【变式2】(24-25七年级上·全国·单元测试)图中线段有 条,射线有 条.
【变式3】(24-25七年级上·全国·课后作业)如图,网格纸中有七个黑点和六个白点,经过同色的三点可以画 条直线.
题型05 直线相交的交点个数问题
【典例5】(23-24七年级上·甘肃庆阳·期末)如图,两条直线相交,有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,则七条直线相交最多有 个交点.
【变式1】(18-19七年级·吉林长春·期末)一平面内,3条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;…;那么,10条直线两两相交,最多有 个交点.
【变式2】(2024七年级·全国·竞赛)某市2013年计划投资160亿同时建设9条地铁轨道线,假设要在每个轨道线交叉口建一个报刊亭,且任意两条轨道线至多交叉一次,那么这样的报刊亭最多可建 个.
【变式3】(2024·湖北孝感·一模)小明学习相交直线时发现:3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,
(1)5条直线两两相交最多有 个交点;
(2)n条直线两两相交最多有 个交点.(用含有字母n的式子表示,)
题型06 画直线、射线、线段
【典例6】(23-24七年级上·新疆喀什·期末)如图,在平面上有A,B,C,D四点,请按照下列语句画出图形.
(1)画直线;
(2)画射线;
(3)连接B,C;
(4)线段和线段相交于点O.
【变式1】(23-24七年级上·吉林延边·期末)已知A,B,C,D四点(如图):
(1)画线段,射线,直线;
(2)连,与直线交于点;
(3)连接,并延长线段与射线交于点;
(4)连接,并延长线段与线段的反向延长线交于点.
【变式2】(22-23七年级上·河南郑州·阶段练习)如图,已知四点A,B,C,D,按下列要求作图:
(1)连接,BD交于点O;
(2)作射线AB,射线CD;
(3)反向延长射线CD交射线AB于点P;
(4)图中有几条线段?几条射线?几条直线?
【变式3】(22-23七年级上·云南昆明·期末)如图所示,平面上有五个点A、B、C、D、E.按下列要求画出图形.
(1)连接;
(2)画直线交于点M;
(3)画射线;
(4)请在直线上确定一点N,使B、E两点到点N的距离之和最小,并说明理由(保留作图痕迹).
一、单选题
1.(2024·河北石家庄·模拟预测)下列各图中,表示“射线”的是( )
A.B.
C.D.
2.(24-25七年级上·全国·课后作业)挂条幅时,要钉两个钉子才能牢固,其中的数学道理是( ).
A.两点之间线段最短B.两点确定一条直线
C.两点能够确定多条直线D.点动成线
3.(22-23六年级下·山东泰安·期中)如图,下列说法正确的是( )
A.直线和直线不是同一条直线
B.点是直线的一个端点
9.(22-23七年级上·甘肃酒泉·期末)素养提升:
如果平面上有个点,且每3个点均不在1条直线上,那么最多画 条直线.
能否通过以上发现,解决问题:某班45名同学在毕业的一次聚会中,若每两人握1次手问好,那么一共要握 次手.
10.(23-24七年级上·湖北武汉·阶段练习)已知2条直线相交,有1个交点,3条直线相交最多有3个交点,4条直线相交最多有6个交点,…,像这样,n条直线相交最多有 个交点.
三、解答题
11.(23-24七年级上·全国·课后作业)如图所示,共有多少条直线、射线、线段?请依次指出.
12.(22-23七年级上·江西上饶·期末)如图,平面内有四个点,根据下列语句画图.
(1)画线段;
(2)画直线;
(3)画射线和.
13.(2024七年级下·云南·专题练习)如图,平面上有四个点,请根据下列语句作图.
(1)画直线BD;
(2)画线段AD与线段相交于点O;
(3)画射线AB与射线CD相交于点P.
14.(23-24七年级上·福建泉州·期末)我们知道,两条直线相交最多有一个交点,三条直线相交最多有三个交点,四条直线相交最多有6个交点,…,如图所示.
(1)五条直线相交最多有______个交点,六条直线相交最多有______个交点;
(2)若有条直线相交,求最多交点的个数.(用含的代数式表示)
15.(23-24六年级下·山东济南·开学考试)若直线上有两个点,则以这两点为端点可以确定 一条线段.请仔细观察图形,解决下列问题:
试验观察:
(1)如图①所示,直线l上有3个点A,B, C,则可以确定 条线段.
(2)如图②所示,直线l上有4个点 A,B, C,D,则可以确定 条线段.
探索归纳:
(3)若直线上有n个点,一共可以确定多少条线段?
(4)如图③所示,由泰山始发终点至青岛的某次列车,运行途中停靠的车站依次是泰山、济南、淄博、潍坊、青岛,那么要为这次列车制作的单程火车票有( )
A.5 种 B.10 种 C.15 种 D.20 种
课程标准
学习目标
①了解直线、射线与线段的概念
②掌握直线、射线、线段的表示方法和画法.
1.了解直线、射线与线段的概念;理解两点确定一条直线的事实;
2.掌握直线、射线、线段的表示方法和画法,以及它们的联系与区别.
名称
直线
射线
线段
图形
B
A
A
B
B
A
端点个数
无
一个
两个
表示法
直线
直线AB(BA)
射线
射线AB
线段
线段AB(BA)
作法叙述
作直线
作直线AB
作射线
作射线AB
作线段
作线段AB
连接AB
延长
向两端无限延长
向一端无限延长
不可延长
第01讲 线段、射线、直线
知识点01 线段、射线、直线的概念
1.线段的表示也有两种:一个小写字母或用端点的两个大写字母.但前面必须加“线段”两字,如:线段a;线段AB.
2.射线的表示同样有两种:一个小写字母或端点的大写字母和射线上的要给大写字母,前面必须加“射线”两字
3.直线的表示有两种:一个小写字母或两个大写字母.但前面必须加“直线”两字,如:直线;直线m,直线AB;直线CD
基本概念:
【即学即练1】
1.(23-24六年级下·全国·假期作业)如图,表示方法正确的是( )
A.①②B.②④C.③④D.①④
【答案】B
【分析】本题主要考查了直线、射线和线段的表示方法,根据直线、射线和线段的表示方法逐项进行判断即可.
【详解】解:不能用一个大写字母表示直线,故①错误;
可以用一个小写字母表示射线,故②正确;
③中的射线应表示为射线,故③错误;
可用表示线段两个端点的大写字母表示线段,故④正确;
综上,表示方法正确的只有②④.
故选:B.
2.(23-24六年级下·山东烟台·期中)在日常生活中,手电筒发射出来的光线,类似于 .(填“折线”或“线段”或“射线”或“直线”)
【答案】射线
【分析】本题主要考查射线的定义,根据直线,射线和线段的区别即可得出答案.
【详解】手电筒可近似看成一个点,所以手电筒发射出来的光线相当于一个从一个端点出发的一条射线,
故答案为:射线.
3.(23-24六年级下·全国·假期作业)根据如图所示的图形填空:
(1)点B在直线_________,点C在直线_________;
(2)点E是直线与_________直线_________的交点,直线与直线相交于点_________;
(3)过点A的直线有_________条,分别是__________________.
【答案】(1)上,外
(2)
(3)3,直线,直线,直线
【分析】本题考查了直线、射线、线段,熟练掌握点与直线的位置关系是解题的关键.
(1)观察图形,根据点与直线的位置关系进行判断即可;
(2)确定经过点E的直线是哪两条即可得出结论;观察图形确定直线与直线的交点即可;
(3)观察图形确定过点A的直线即可解答.
【详解】(1)解:点B在直线上,点C在直线外,
故答案为:上,外;
(2)解:点E是直线与直线的交点,直线与直线相交于点F,
故答案为:;
(3)解:过A点的直线有3条,分别是直线,直线,直线,
故答案为:3,直线,直线,直线.
知识点02 直线的性质
经过两点有一条直线,并且只有一条直线.简单地:两点确定一条直线. 两条直线相交,只有一个交点.
【即学即练2】
1.(23-24七年级上·贵州贵阳·期末)墨斗被认为是“百作手艺祖师爷”鲁班的发明,是木匠用来弹、放各种线记的重要工具,以其“绳之以墨”的功能成为了文人墨客心中正直的化身.如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 .
【答案】两点确定一条直线
【分析】本题主要考查两点确定一条直线,熟练掌握这一知识点是解题的关键.根据题意可直接进行求解.
【详解】解:由题意得:能解释这一实际应用的数学知识是两点确定一条直线.
故答案为:两点确定一条直线.
题型01 直线、射线、线段的联系与区别
【典例1】(2024·河北邢台·三模)下列图形中,可以表示为“线段”的是( )
A.B.
C.D.
【答案】A
【知识点】直线、射线、线段的联系与区别
【分析】根据线段的性质即可得解.线段是直线的一部分,有两个端点.熟练掌握线段的性质是解题的关键.
【详解】A、是直线,不符合题意;
B、是射线,不符合题意;
C、是线段,符合题意;
D、是射线,不符合题意;
.
【变式1】(23-24六年级下·全国·假期作业)图中直线的表示方法,不正确的有( )
A.1个B.2个C.3个D.4个
【答案】D
【知识点】直线、射线、线段的联系与区别
【分析】本题主要考查了直线的表示方法,一条直线可以用两个大写字母或一个小写字母表示,根据直线的表示方法进行判断即可.
【详解】解:图中直线、、、A表述错误,直线表示正确,因此图中直线的表示方法,不正确的有4个.
故选:D.
【变式2】(23-24七年级上·河南平顶山·期末)如图,对于图中直线的描述,正确的是( )
A.图中有直线B.图中有直线
C.直线与直线交于点OD.直线与直线m交于点O
【答案】D
【知识点】直线、射线、线段的联系与区别
【分析】本题考查的是直线的表述方法,直线与直线的交点的含义,根据直线的表示方法逐一判断即可.
【详解】解:图中有直线,直线,直线,直线,
直线与直线交于点O,直线与直线m交于点O,
∴A,B,C错误,不符合题意;D正确,符合题意;
故选:D.
【变式3】(23-24七年级上·全国·单元测试)小明根据下列语句,分别画出了图形,并将图形的标号填在了相应的“语句”后面的横线上.其中正确的是( )
①直线经过点三点,并且点在点与之间;
②点在线段的反向延长线上;
③点是直线外一点,过点的直线与直线相交于点;
④直线相交于点.
A.①②③④B.①②④C.①③④D.②③
【答案】D
【知识点】直线、射线、线段的联系与区别
【分析】本题考查了直线,射线和线段的知识,熟练掌握以上知识是解题的关键.
根据直线是向两方无限延伸、射线是向一方无限延伸和线段不能向任何一方延伸的定义分析即可.
【详解】解:①直线经过点三点,并且点在点与之间,,正确;
②点在线段的反向延长线上,,正确;
③点是直线外一点,过点的直线与直线相交于点,,正确;
④直线相交于点,,正确;
故选A.
题型02 点与线的位置关系
【典例2】(23-24七年级上·河北唐山·期末)平面上有A,B,C三点,如果,,,那么下列说法正确的是( )
A.点C在线段上B.点C在线段的延长线上
C.点C在直线外D.点C的位置无法确定
【答案】D
【知识点】点与线的位置关系
【分析】本题考查线段、射线、直线的意义,理解点与直线的位置关系是解决问题的关键.根据,,,有进行判断即可.
【详解】解:如图,在平面内,,
∵,,
∴点C为以A为圆心,6为半径,与以B为圆心,4为半径的两个圆的交点,
由于,
所以,点C在线段上,
.
【变式1】(23-24七年级上·吉林·期末)如图,直线m和直线n相交于点O,对于图形,说法正确的语句有( )
①点O在直线m上.
②点O在直线n上.
③点O在直线m上. 也在直线n上.
④直线m经过点O.
A.1个.B.2个.C.3个.D.4个.
【答案】D
【知识点】点与线的位置关系
【分析】题考查直线、线段、射线的画法,解题的关键是根据点与直线的位置关系进行判断得出答案.
【详解】解:①点O在直线m上,说法正确;
②点O在直线n上,说法正确;
③点O在直线m上,也在直线n上,说法正确;
④直线m经过点O,说法正确;
故选D.
【变式2】(23-24七年级上·河北石家庄·阶段练习)下列几何图形与相应语言描述不相符的是( )
A.如图甲所示,直线不经过点P
B.如图乙所示,直线a与直线b交于点O
C.如图丙所示,点C在线段上
D.如图丁所示,线段与射线一定相交
【答案】A
【知识点】画出直线、射线、线段、点与线的位置关系
【分析】本题考查的是直线,射线,线段的含义,点与直线,射线,线段的位置关系,理解作图语言是解本题的关键.
【详解】解:如图甲所示,直线不经过点P,描述正确,故A不符合题意;
如图乙所示,直线a与直线b交于点O,描述正确,故B不符合题意;
如图丙所示,点C在直线上,原描述错误,故C符合题意;
如图丁所示,线段与射线一定相交,描述正确,故D不符合题意;
故选C
【变式3】(2023七年级上·江苏·专题练习)如图,用适当的语句表述图中点与直线的关系,错误的是( )
A.点P在直线外B.点C在直线外
C.直线不经过点MD.直线经过点B
【答案】B
【知识点】点与线的位置关系
【分析】本题考查的是点与直线的位置关系,理解点在直线上,点在直线外,再逐一分析即可得到答案.
【详解】解:点P在直线外,描述正确,故A不符合题意;
点C在直线上,故B符合题意;
线不经过点M,描述正确,故C不符合题意;
直线经过点B,描述正确,故D不符合题意;
故选B
题型03 两点确定一条直线
【典例3】(23-24六年级下·山东东营·开学考试)要在墙壁上固定一根小木条,至少需要两枚钉子,其数学原理是 .
【答案】两点确定一条直线
【知识点】两点确定一条直线
【分析】本题考查直线的性质,熟练掌握直线的性质是解题的关键;
根据直线的性质即可求解;
【详解】解:要在墙壁上固定一根小木条,至少需要两枚钉子,其数学原理是:两点确定一条直线.
故答案为:两点确定一条直线.
【变式1】(23-24七年级上·河南新乡·期末)如图,木匠师傅经过刨平的木板上的A,B两点,可以弹出一条笔直的墨线,请你解释这一实际应用的数学基本事实是 .
【答案】两点确定一条直线
【知识点】两点确定一条直线
【分析】本题主要考查了两点确定一条直线.根据两点确定一条直线,即可求解.
【详解】解:解释这一实际应用的数学基本事实是两点确定一条直线.
故答案为:两点确定一条直线
【变式2】(23-24六年级下·山东青岛·阶段练习)要种一列排列笔直的树,小明说:只要先定下两棵树的位置,然后其他树的位置就容易确定了,你认为小明这样说根据的数学原理是 .
【答案】两点确定一条直线
【知识点】两点确定一条直线
【分析】本题考查了直线的性质,根据公理“两点确定一条直线”来解答即可.
【详解】解:要种一列排列笔直的树,小明说:只要先定下两棵树的位置,然后其他树的位置就容易确定了,你认为小明这样说根据的数学原理是两点确定一条直线,
故答案为:两点确定一条直线.
【变式3】(23-24七年级上·福建厦门·期末)暑假期间,小华参加了夏令营打靶瞄准训练,如图所示,打靶瞄准用到的数学原理是 .
【答案】两点确定一条直线
【知识点】两点确定一条直线
【分析】本题考查直线的性质,掌握“两点确定一条直线”的基本事实是正确判断的关键.根据“两点确定一条直线”进行判断即可.
【详解】解:打靶瞄准用到的数学原理是:两点确定一条直线.
故答案为:两点确定一条直线.
题型04 直线、线段、射线的数量问题
【典例4】(23-24七年级上·河南郑州·期末)如图,小金同学根据图形写出了三个结论:①图中共有6条线段;②图中共有1条直线;③图中射线与射线不是同一条射线.其中结论正确的是( )
A.①②B.①③C.②③D.①②③
【答案】D
【知识点】直线、射线、线段的联系与区别、直线、线段、射线的数量问题
【分析】此题主要考查了线段、射线、直线的定义,准确识图,理解线段、射线、直线的定义是解决问题的关键.
【详解】解:图中有线段,,,,,共6条,
∴结论①正确;
图中共有一条直线,
∴结论②正确;
图中射线可表示为射线,
∴图中射线与射线是同一条射线,
∴结论③不正确.
综上所述:正确的结论是①②.
.
【变式1】(23-24七年级上·四川成都·开学考试)图中,共有 条线段.
【答案】15
【知识点】直线、线段、射线的数量问题
【分析】本题考查了线段的数量问题.
线段有两个端点,而两个端点间的距离就是这条线段的长度,据此数出两个端点之间的线段即可.
【详解】解:图中共有6个端点,则共有线段(条).
故答案为:15.
【变式2】(24-25七年级上·全国·单元测试)图中线段有 条,射线有 条.
【答案】 6 4
【知识点】直线、线段、射线的数量问题
【分析】本题主要考查学生对线段和射线的认识,注意不要数重或漏数.根据线段和射线的意义分类数一数即可.
【详解】解:线段有:、、、、、,共6条;
射线有:、、、,共4条;
故答案为:6,4.
【变式3】(24-25七年级上·全国·课后作业)如图,网格纸中有七个黑点和六个白点,经过同色的三点可以画 条直线.
【答案】3
【知识点】直线、线段、射线的数量问题
【分析】本题考查了直线,根据直线的特点在图中画出满足条件的直线,即可作答.
【详解】作图如下:
经过同色的三点可以画3条直线,
故答案为:3.
题型05 直线相交的交点个数问题
【典例5】(23-24七年级上·甘肃庆阳·期末)如图,两条直线相交,有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,则七条直线相交最多有 个交点.
【答案】21
【知识点】图形类规律探索、直线相交的交点个数问题
【分析】本题考查了图形的变化,是一道关于数字猜想的问题,关键是通过归纳与总结,得到其中的规律.
四条直线相交最多的交点个数可通过画图得出交点个数,通过继续增加直线的条数可以找出规律即可解答;
【详解】解: 如图,两条直线相交最多有1个交点,即;
三条直线相交最多有3个交点,即;
四条直线相交最多有6个交点,即,
五条直线相交最多有10个交点,即,
……
∴n条直线两两相交,最多有个交点(n为正整数,且).
∴当时,最多有个交点
故答案为:.
【变式1】(18-19七年级·吉林长春·期末)一平面内,3条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;…;那么,10条直线两两相交,最多有 个交点.
【答案】
【知识点】直线相交的交点个数问题
【分析】此题考查的知识点是相交线,关键是此题在相交线的基础上,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊到一般猜想的方法.由已知一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点总结出:在同一平面内,n条直线两两相交,则有个交点,代入即可求解.
【详解】解:∵3条直线两两相交,最多有3个交点;而;
4条直线两两相交,最多有6个交点;而,
5条直线两两相交,最多有10个交点;…;而,
∴在同一平面内,n条直线两两相交,则最多有 个交点,
∴10条直线两两相交,交点的个数最多为 .
故答案为:.
【变式2】(2024七年级·全国·竞赛)某市2013年计划投资160亿同时建设9条地铁轨道线,假设要在每个轨道线交叉口建一个报刊亭,且任意两条轨道线至多交叉一次,那么这样的报刊亭最多可建 个.
【答案】36
【知识点】直线相交的交点个数问题
【分析】此问题相当于“9条直线相交,最多有几个交点”的问题,利用公式直接计算即可.
【详解】∵9条地铁轨道线相当于有9条直线,每一条直线最多与其它直线有8个交点,
∴最多有个交点,即这样的报亭最多有个,
故答案为:.
【变式3】(2024·湖北孝感·一模)小明学习相交直线时发现:3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,
(1)5条直线两两相交最多有 个交点;
(2)n条直线两两相交最多有 个交点.(用含有字母n的式子表示,)
【答案】 10
【知识点】数字类规律探索、直线相交的交点个数问题
【分析】本题考查了规律型—数字的变化类;根据所给数据,发现规律:n条直线两两相交,最多有个交点,然后进行计算即可.
【详解】解:(1)∵两条直线最多有1个交点,
∴有n条直线,每一条直线与其他条直线都最多有1个交点,且两条直线的交点只算作一个,
∴有n条直线,两两相交最多有个交点,
∴5条直线两两相交最多有个交点,
故答案为:10;
(2)由(1)得n条直线两两相交最多有个交点,
故答案为:.
题型06 画直线、射线、线段
【典例6】(23-24七年级上·新疆喀什·期末)如图,在平面上有A,B,C,D四点,请按照下列语句画出图形.
(1)画直线;
(2)画射线;
(3)连接B,C;
(4)线段和线段相交于点O.
【答案】(1)见详解
(2)见详解
(3)见详解
(4)见详解
【知识点】画出直线、射线、线段
【分析】本题主要考查了作图,作直线,射线,线段,以及两线段的交点等作图知识.
(1)过点A、B作直线,要向两方延伸;
(2)过B、D作射线,向D点方向延伸,B点方向不延伸∶
(3)就是作线段;
(4)连接、交点标注为O;
【详解】(1)解:直线如下图所示:
(2)解:射线如下图所示:
(3)解:线段如下图所示:
(4)解:线段和线段相交于点O如下图所示:
【变式1】(23-24七年级上·吉林延边·期末)已知A,B,C,D四点(如图):
(1)画线段,射线,直线;
(2)连,与直线交于点;
(3)连接,并延长线段与射线交于点;
(4)连接,并延长线段与线段的反向延长线交于点.
【答案】(1)见解析
(2)见解析
(3)见解析
(4)见解析
【知识点】画出直线、射线、线段
【分析】本题主要考查了直线、射线、线段的特征,准确掌握直线、线段、射线的特征是解题的关键,属于基础题.
(1)根据直线,射线,线段的特征可作图求解;
(2)根据直线,射线,线段的特征可作图求解;
(3)根据直线,射线,线段的特征可作图求解;
(4)根据直线,射线,线段的特征可作图求解.
【详解】(1)解:根据题意画出图如图所示;
(2)解:根据题意画出图如图所示;
(3)解:根据题意画出图如图所示;
(4)解:根据题意画出图如图所示.
【变式2】(22-23七年级上·河南郑州·阶段练习)如图,已知四点A,B,C,D,按下列要求作图:
(1)连接,BD交于点O;
(2)作射线AB,射线CD;
(3)反向延长射线CD交射线AB于点P;
(4)图中有几条线段?几条射线?几条直线?
【答案】(1)见解析
(2)见解析
(3)见解析
(4)有线段共条,射线条,直线条
【知识点】画出直线、射线、线段
【分析】本题考查了复杂作图,掌握直线、线段和射线的意义是解题的关键.
(1)根据线段的特点作图;
(2)根据射线的特点作图;
(3)根据射线的特点作图;
(4)根据线段、直线、射线的意义求解.
【详解】(1)如图:线段,点即为所求;
(2)如图:射线即为所求;
(3)点即为所求;
(4)图中有线段共条,射线条,直线条.
【变式3】(22-23七年级上·云南昆明·期末)如图所示,平面上有五个点A、B、C、D、E.按下列要求画出图形.
(1)连接;
(2)画直线交于点M;
(3)画射线;
(4)请在直线上确定一点N,使B、E两点到点N的距离之和最小,并说明理由(保留作图痕迹).
【答案】(1)见解析
(2)见解析
(3)见解析
(4)见解析,理由见解析
【知识点】两点之间线段最短、画出直线、射线、线段
【分析】本题考查了画直线、射线、线段,两点之间线段最短.掌握直线、射线、线段的定义及画法是解题关键.
(1)根据线段的定义作图即可;
(2)根据直线的定义作图即可;
(3)根据射线的定义作图即可;
(4)连接,由两点间线段最短可知,与的额交点即为点.
【详解】(1)解:如图,线段即为所求作;
(2)解:如图,点M即为所求作;
(3)解:射线即为所求作;
(4)解:如图,点即为所求作;
理由为:两点间线段最短.
一、单选题
1.(2024·河北石家庄·模拟预测)下列各图中,表示“射线”的是( )
A.B.
C.D.
【答案】B
【知识点】直线、射线、线段的联系与区别
【分析】本题考查了射线的定义,射线是指由线段的一端无限延长所形成的直的线,射线仅有一个端点,无法测量,射线是指端点在点A上,据此即可作答.
【详解】解:依题意,
射线是指射线的端点在点A上.
故选:B.
2.(24-25七年级上·全国·课后作业)挂条幅时,要钉两个钉子才能牢固,其中的数学道理是( ).
A.两点之间线段最短B.两点确定一条直线
C.两点能够确定多条直线D.点动成线
【答案】B
【知识点】两点确定一条直线
【分析】本题考查了两点确定一条直线,熟练掌握直线的性质是解题的关键;经过两点有且只有一条直线,简称:两点确定一条直线; 根据两点确定一条直线解答即可.
【详解】解:挂条幅时,要钉两个钉子才能牢固,其中的数学道理是:两点确定一条直线,
故选:
3.(22-23六年级下·山东泰安·期中)如图,下列说法正确的是( )
A.直线和直线不是同一条直线
B.点是直线的一个端点
C.射线和射线不是同一条射线
D.点在线段上
【答案】D
【知识点】直线、射线、线段的联系与区别
【分析】本题主要考查了直线,射线,线段的定义.根据直线,射线,线段的定义,逐项判断即可求解.
【详解】解:A.直线和直线是同一条直线,故本选项错误,不符合题意;
B.直线没有端点,故本选项错误,不符合题意;
C.射线和射线是同一条射线,故本选项错误,不符合题意;
D.点在线段上,故本选项正确,符合题意;
故选:D.
4.(23-24七年级上·山东聊城·阶段练习)下列说法错误的是( )
A. 直线l经过点AB. 点C在线段上
C. 射线与线段有公共点D. 直线a,b相交于点A
【答案】B
【知识点】直线、射线、线段的联系与区别、点与线的位置关系、直线相交的交点个数问题
【分析】根据点和直线的位置关系,相交线的有关内容判断即可.
【详解】解:A、由图可得,点A在直线l上,故直线l经过点A,故本选项不符合题意;
B、由图可得,点C在线段的上方,故点A不在线段上,故本选项符合题意;
C、由图可得,射线与线段有交点,故射线与线段有公共点,故本选项不符合题意;
D、由图可得,点A为直线a、b的公共点,故直线a、b相交于点A,故本选项不符合题意.
故选:B.
【点睛】本题考查了直线、射线、线段的应用,主要考查学生的理解能力和应用能力,应用了数形结合思想.
5.(23-24七年级上·山东德州·期末)如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点.点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P最多有( )个.
A.3B.4C.5D.6
【答案】A
【知识点】直线、线段、射线的数量问题、与线段有关的动点问题
【分析】本题考查的是直线与线段的相关内容,正确理解题意、利用转化的思想去思考线段的总条数是解决问题的关键,可以减少不必要的分类.点P与A,B,C,D四点中的至少两个点距离相等时,也就是点P恰好是其中一条线段中点.而图中共有线段5条,所以出现报警次数最多5次.
【详解】解:由题意知,当P点经过任意一条线段中点的时候会发出警报,
∵图中共有线段、、、、,
∴发出警报的点P最多有5个.
.
二、填空题
6.(23-24七年级上·福建福州·期末)如图,建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙,读用所学的数学知识解释它这样操作的原因是
【答案】两点确定一条直线
【知识点】两点确定一条直线
【分析】此题主要考查直线的性质:两点确定一条直线,熟记性质是解题的关键.
【详解】建筑工人砌墙时经常先在两端立桩、拉线,然后沿着线砌出笔直的墙,其依据的基本事实是两点确定一条直线.
故答案为:两点确定一条直线.
7.(24-25七年级上·全国·课后作业)如图,是直线l上的三个点.
(1)图中共有 条线段;
(2)图中以点B为端点的射线有 条,分别是 ;
(3)直线l还可以表示为 .
【答案】 3 2 射线、射线 直线或直线或直线或直线或直线或直线
【知识点】直线、射线、线段的联系与区别
【分析】此题主要考查了线段、直线、射线,关键是掌握线段的定义.
(1)根据线段概念即可求得答案;
(2)根据射线概念即可求得答案;
(3)根据直线的概念即可求得答案.
【详解】解:(1)图中共有3条线段,线段、线段、线段;
故答案为:3;
(2)图中以点B为端点的射线有2条,射线、射线;
故答案为:2,射线、射线;
(3)直线l还可以表示为:直线或直线或直线或直线或直线或直线;
故答案为:直线或直线或直线或直线或直线或直线.
8.(22-23七年级上·河南开封·期末)直线的位置关系如图所示,下列语句:①点在直线上;②直线经过点;③直线交于点;④点在直线AB外;⑤直线两两相交.以上表述正确的有 .(只填写序号)
【答案】②③④⑤
【知识点】点与线的位置关系、相交线
【分析】本题考查了点和直线的位置关系,直线和直线的位置关系,根据图性逐项判断即可求解,正确识图是解题的关键.
【详解】解:由图可知,点在直线外,故①错误;
由图可知,直线经过点,故②正确;
由图可知,直线交于点,故③正确;
由图可知,点在直线AB外,故④正确;
由图可知,直线两两相交,故⑤正确;
∴以上表述正确的有②③④⑤,
故答案为:②③④⑤.
9.(22-23七年级上·甘肃酒泉·期末)素养提升:
如果平面上有个点,且每3个点均不在1条直线上,那么最多画 条直线.
能否通过以上发现,解决问题:某班45名同学在毕业的一次聚会中,若每两人握1次手问好,那么一共要握 次手.
【答案】 990
【知识点】直线、线段、射线的数量问题
【分析】本题主要考查规律型图形的变化类,根据每一个点可以与其他个点分别连接生成条直线,去掉重复的即可得到个点(每3个点均不在1条直线上),最多画(条直线.根据每一个人可以与其他44握手一次,每人44次,即可求解.
【详解】∵每一个点可以与其他个点连接生成条直线,
∴个点最多画直线数量为
∵某班45名同学在毕业的一次聚会中,若每两人握1次手问好,则每一个人可以与其他44握手一次,每人44次,
∴45人一共要握手(次.
故答案为:,990.
10.(23-24七年级上·湖北武汉·阶段练习)已知2条直线相交,有1个交点,3条直线相交最多有3个交点,4条直线相交最多有6个交点,…,像这样,n条直线相交最多有 个交点.
【答案】
【知识点】数字类规律探索、直线相交的交点个数问题
【分析】此题考查的是相交线及规律性题目,解答此题关键是根据直线的条数变化得到的交点个数的变化,得出规律,再利用规律进行计算即可解答问题.
2条直线相交有1个交点,3条直线相交最多有个交点,4条直线相交最多有个交点..........按这样的规律,条直线相交的交点最多是个交点.
【详解】解:2条直线相交有1个交点,
(3)见解析
【知识点】画出直线、射线、线段
【分析】本题考查了对直线、射线、线段定义的应用,主要考查学生的理解能力和画图能力.
(1)根据线段的定义画出即可;
(2)根据直线的定义画出即可;
(3)根据射线的定义画出即可.
【详解】(1)解:如图所示,线段为所求;
(2)解:如图所示,直线为所求;
(3)解:如图所示,射线和为所求.
13.(2024七年级下·云南·专题练习)如图,平面上有四个点,请根据下列语句作图.
(1)画直线BD;
(2)画线段AD与线段相交于点O;
(3)画射线AB与射线CD相交于点P.
【答案】(1)见解析
(2)见解析
(3)见解析
【知识点】画出直线、射线、线段
【分析】本题考查画直线、射线、线段,根据直线、射线、线段的定义画出图形即可.
(1)作直线BD即可;
(2)作线段AD与线段,交点标记为O即可;
(3)作射线AB与射线CD,交点标记为P即可.
【详解】(1)解:直线BD如图所示;
(2)线段AD与线段相交于点O,如图所示;
(3)射线AB与射线CD相交于点P,如图所示.
14.(23-24七年级上·福建泉州·期末)我们知道,两条直线相交最多有一个交点,三条直线相交最多有三个交点,四条直线相交最多有6个交点,…,如图所示.
(1)五条直线相交最多有______个交点,六条直线相交最多有______个交点;
(2)若有条直线相交,求最多交点的个数.(用含的代数式表示)
【答案】(1)10;15
(2)有条直线相交,最多交点的个数为.
【知识点】图形类规律探索、直线相交的交点个数问题
【分析】此题考查图形规律的探究.
(1)根据图形相邻两个图形的交点个数的差为从2开始的连续整数,然后列式计算即可得解;
(2)根据(1)得到的规律,即可得解.
【详解】(1)解:三条直线交点最多为个,
四条直线交点最多为个,
五条直线交点最多为个,
六条直线交点最多为个;
故答案为:10;15;
(2)解:n条直线交点最多为.
答:有条直线相交,最多交点的个数为.
15.(23-24六年级下·山东济南·开学考试)若直线上有两个点,则以这两点为端点可以确定 一条线段.请仔细观察图形,解决下列问题:
试验观察:
(1)如图①所示,直线l上有3个点A,B, C,则可以确定 条线段.
(2)如图②所示,直线l上有4个点 A,B, C,D,则可以确定 条线段.
探索归纳:
(3)若直线上有n个点,一共可以确定多少条线段?
(4)如图③所示,由泰山始发终点至青岛的某次列车,运行途中停靠的车站依次是泰山、济南、淄博、潍坊、青岛,那么要为这次列车制作的单程火车票有( )
A.5 种 B.10 种 C.15 种 D.20 种
【答案】(1)3(2)6(3)(4)B
【知识点】画出直线、射线、线段、直线、线段、射线的数量问题
【分析】(1)直接利用线段的定义即可得到结论.
(2)直接利用线段的定义即可得到结论.
(3)根据(1)、(2)得到的结论进行解答.
(4)单程两个站点有一种票,相当于两两组合,由结论式来解答.
此题考查直线、线段、射线,关键是掌握结论式.以及根据直线、线段、射线的区别解答.
【详解】解:(1)直线上有、、,线段总条数是:,
故答案为:3;
(2)若直线上有四个点、、、,线段总条数是:,
故答案为:6;
(3)若直线上有个点时,线段总条数.
(4)解:(种,
要为这次列车制作的单程火车票10种.
故选:B.
课程标准
学习目标
①了解直线、射线与线段的概念
②掌握直线、射线、线段的表示方法和画法.
1.了解直线、射线与线段的概念;理解两点确定一条直线的事实;
2.掌握直线、射线、线段的表示方法和画法,以及它们的联系与区别.
名称
直线
射线
线段
图形
B
A
A
B
B
A
端点个数
无
一个
两个
表示法
直线
直线AB(BA)
射线
射线AB
线段
线段AB(BA)
作法叙述
作直线
作直线AB
作射线
作射线AB
作线段
作线段AB
连接AB
延长
向两端无限延长
向一端无限延长
不可延长
北师大版2024-2025学年七年级数学上册同步讲义第4章第02讲比较线段的长短(学生版+解析): 这是一份北师大版2024-2025学年七年级数学上册同步讲义第4章第02讲比较线段的长短(学生版+解析),共58页。学案主要包含了即学即练1,即学即练2,即学即练3,即学即练4,即学即练5等内容,欢迎下载使用。
北师大版2024-2025学年七年级数学上册同步讲义第3章第01讲代数式(学生版+解析): 这是一份北师大版2024-2025学年七年级数学上册同步讲义第3章第01讲代数式(学生版+解析),共32页。学案主要包含了即学即练1,即学即练2,即学即练3等内容,欢迎下载使用。
北师大版2024-2025学年七年级数学上册同步讲义第2章第01讲有理数(学生版+解析): 这是一份北师大版2024-2025学年七年级数学上册同步讲义第2章第01讲有理数(学生版+解析),共28页。学案主要包含了即学即练1等内容,欢迎下载使用。