
2022-2023学年吉林省长春市经开区洋浦学校九年级(上)期中数学试卷
展开
这是一份2022-2023学年吉林省长春市经开区洋浦学校九年级(上)期中数学试卷,共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
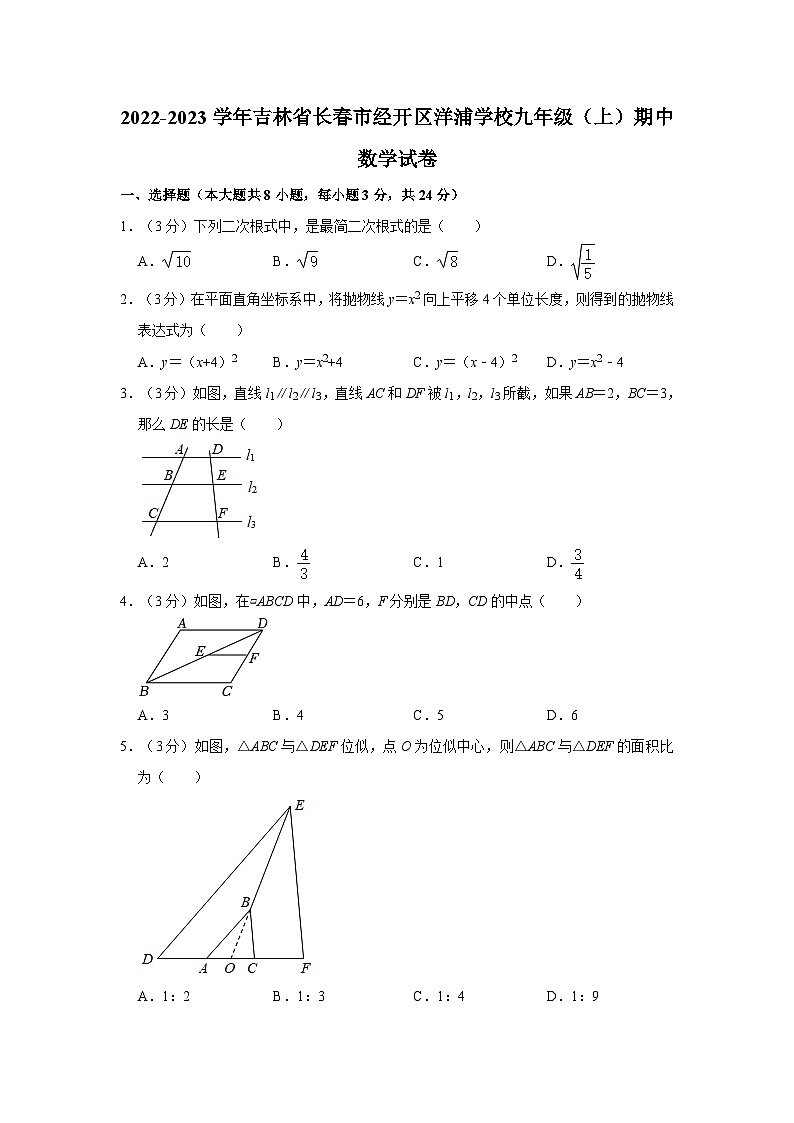
1.(3分)下列二次根式中,是最简二次根式的是( )
A.B.C.D.
2.(3分)在平面直角坐标系中,将抛物线y=x2向上平移4个单位长度,则得到的抛物线表达式为( )
A.y=(x+4)2B.y=x2+4C.y=(x﹣4)2D.y=x2﹣4
3.(3分)如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=2,BC=3,那么DE的长是( )
A.2B.C.1D.
4.(3分)如图,在▱ABCD中,AD=6,F分别是BD,CD的中点( )
A.3B.4C.5D.6
5.(3分)如图,△ABC与△DEF位似,点O为位似中心,则△ABC与△DEF的面积比为( )
A.1:2B.1:3C.1:4D.1:9
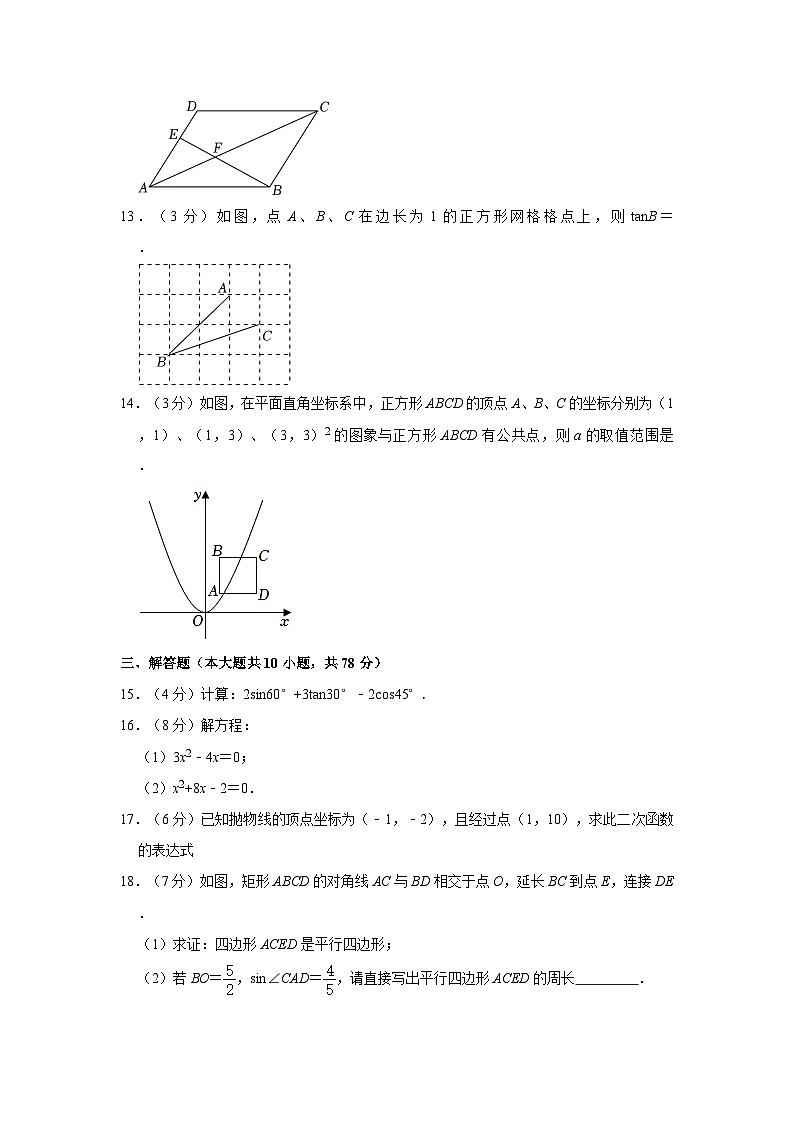
6.(3分)如图是净月潭国家森林公园一段索道的示意图.已知A、B两点之间的距离为35米,∠A=α,则缆车从A点到达B点(BC的长)为( )
A.35sinα米B.米C.35csα米D.米
7.(3分)已知二次函数y=﹣x2+2x+1,若y随x的增大而增大,则x的取值范围是( )
A.x≥1B.x≤1C.x≥﹣1D.x≤﹣1
8.(3分)已知二次函数y=x2+2x﹣4,当﹣3<x≤0时,y的取值范围是( )
A.﹣4≤y≤﹣1B.﹣4≤y<﹣1C.﹣5≤y<﹣1D.﹣5≤y≤﹣4
二、填空题(本大题共6小题,每小题3分,共18分)
9.(3分)若,则= .
10.(3分)已知△ABC,P是边AB上的一点,连接CP,使△ACP∽△ABC,这个条件可以是 .(写出一个即可)
11.(3分)如图,某同学利用标杆BE测量教学楼的高度,已知标杆BE高1.5m,BC=12.8m,则教学楼CD的高度是 m.
12.(3分)如图,在▱ABCD中,点E在边AD上,BE与AC交于点F.若AC=20,则AF的长为 .
13.(3分)如图,点A、B、C在边长为1的正方形网格格点上,则tanB= .
14.(3分)如图,在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为(1,1)、(1,3)、(3,3)2的图象与正方形ABCD有公共点,则a的取值范围是 .
三、解答题(本大题共10小题,共78分)
15.(4分)计算:2sin60°+3tan30°﹣2cs45°.
16.(8分)解方程:
(1)3x2﹣4x=0;
(2)x2+8x﹣2=0.
17.(6分)已知抛物线的顶点坐标为(﹣1,﹣2),且经过点(1,10),求此二次函数的表达式
18.(7分)如图,矩形ABCD的对角线AC与BD相交于点O,延长BC到点E,连接DE.
(1)求证:四边形ACED是平行四边形;
(2)若BO=,sin∠CAD=,请直接写出平行四边形ACED的周长 .
19.(7分)二次函数y=ax2+bx+c(a≠0)的函数值y与自变量x之间的部分对应值如下表:
(1)求出抛物线的函数表达式.
(2)当y=ax2+bx+c(a≠0)的图象上有两点A(﹣7,y1),B(﹣8,y2),则y1 y2.(填“>”、“=”或“<”)
20.(7分)如图,图①、图②、图③均为4×2的正方形网格,△ABC的顶点均在格点上.按要求在图②、图③中各画一个顶点在格点上的三角形.
要求:
(1)所画的两个三角形都与△ABC相似但都不与△ABC全等.
(2)图②和图③中新画的三角形不全等.
21.(8分)如图,AC、BD交于点E,BC=CD
(1)求证:△AEB∽△CED;
(2)若BC=12,EC=6,AE=4
22.(9分)感知:如图①,在四边形ABCD中,AB∥CD,点P在BC边上,当∠APD=90°时 (填“是”或“否”).
探究:如图②,在四边形ABCD中,点P在BC边上,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,
BC=,CE=9,则DE的长为 .
23.(10分)如图,在平面直角坐标系中,抛物线y=(点A在点B的左侧),第一象限内的点C在该抛物线上.
(1)直接写出A、B两点的坐标;
(2)若△ABC的面积为12,求点C坐标;
(3)在第(2)问的条件下,直线y=mx+n经过点A、C,当,直接写出x的取值范围.
24.(12分)如图,在Rt△ABC中,∠ACB=90°,BC=3,动点P从点A出发沿AC方向以每秒5个单位长度的速度向终点C运动,过点P作PQ⊥AB于点Q,将线段PQ绕点P逆时针旋转90°得到线段PR
(1)线段AP的长为 (用含t的代数式表示).
(2)当点R落在BC边上时,求t的值.
(3)当C、R、Q三点共线时,求t的值.
(4)当△CPR为钝角三角形时,直接写出t的取值范围.
2022-2023学年吉林省长春市经开区洋浦学校九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共8小题,每小题3分,共24分)
1.【分析】根据最简二次根式的定义直接判断即可.
【解答】解:A. 是最简二次根式;
B. =3,不符合题意;
C. ,不是最简二次根式;
D. ,不是最简二次根式.
故选:A.
【点评】本题考查了最简二次根式,解题关键是正确理解最简二次根式的定义,最简二次根式必须满足:被开方数不含分母,被开方数不含能开得尽方的因数或因式.
2.【分析】根据“上加下减”的原则进行解答即可.
【解答】解:将抛物线y=x2先向上平移4单位长度,
得到的抛物线的解析式是:y=x3+4.
故选:B.
【点评】此题主要考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.
3.【分析】根据平行线分线段成比例定理得出比例式,代入求出即可.
【解答】解:∵直线l1∥l2∥l4,
∴=,
∵AB=2,BC=3,
∴=,
∴DE=,
故选:B.
【点评】本题考查了平行线分线段成比例定理,能根据平行线分线段成比例定理得出正确的比例式是解此题的关键.
4.【分析】根据平行四边形的性质可得BC=AD=6,根据中位线的性质即可求解.
【解答】解:∵在▱ABCD中,AD=6,
∴BC=AD=6,
∵点E,F分别是BD,
∴.
故选:A.
【点评】本题考查了平行四边形的性质,三角形中位线的性质,掌握三角形中位线的性质是解题的关键.
5.【分析】根据位似图形的概念得到AB∥DE,根据相似三角形的性质计算,得到答案.
【解答】解:∵OA:AD=1:2,
∴=,
∵△ABC与△DEF位似,
∴AB∥DE,
∴△OBA∽△OED,
∴==,即△ABC与△DEF的相似比为,
∴△ABC与△DEF的面积比=()2=,
故选:D.
【点评】本题考查的是位似图形的概念和性质,掌握位似图形的概念、相似三角形的面积比等于相似比的平方是解题的关键.
6.【分析】在Rt△ABC中,已知∠BAC和斜边AB,求∠BAC的对边,选择∠BAC的正弦,列出等式即可表示出来.
【解答】解:在Rt△ABC中,,
即,
故选:A.
【点评】本题考查解直角三角形,根据解三角函数的定义,列出方程是解题关键.
7.【分析】由抛物线开口向上,对称轴为直线x=1可知当x≤1时,根据抛物线的性质,在对称轴左侧y随x的增大而增大.
【解答】解:∵y=﹣x2+2x+8,
∴抛物线开口向下,对称轴为:x=﹣,
∴二次函数y=﹣x2+2x+2,当x≤1时.
故选:B.
【点评】此题主要考查了二次函数的性质和应用,要熟练掌握,解答此题的关键是要明确:当抛物线开口向下时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.
8.【分析】根据二次函数的性质和x的取值范围,可以得到相应的y的取值范围,本题得以解决.
【解答】解:∵二次函数y=x2+2x﹣6=(x+1)2﹣3,
∴该函数的对称轴是直线x=﹣1,函数图象开口向上,取得最小值﹣5,
∵﹣6﹣(﹣3)=2,6﹣(﹣1)=1,
∴当﹣6<x≤0时,y的取值范围是﹣5≤y<﹣5,
故选:C.
【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.
二、填空题(本大题共6小题,每小题3分,共18分)
9.【分析】由比例的基本性质,可得4a=3b,进而得,代入计算即可.
【解答】解:∵,
∴3a=3b,
∴,
将其代入得:
原式=,
故答案为:.
【点评】本题考查了比例的性质,及分式的化简计算,如何利用比例关系进行代换是解题的关键.
10.【分析】根据相似三角形的判定方法解决问题即可.
【解答】解:∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB或=时,
故答案为:∠ACP=∠B,或∠APC=∠ACB或=.
【点评】本题考查相似三角形的判定,解题的关键是熟练掌握基本知识,属于中考常考题型.
11.【分析】根据题意和图形,利用三角形相似,可以计算出CD的长,从而可以解答本题.
【解答】解:∵EB⊥AC,DC⊥AC,
∴EB∥DC,
∴△ABE∽△ACD,
∴,
∵BE=1.5m,AB=7.2m,
∴AC=AB+BC=14m,
∴,
解得,DC=17.4,
即教学楼CD的高是17.5m,
故答案为:17.5.
【点评】本题考查相似三角形的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
12.【分析】由平行四边形的性质可得AD∥BC,AD=BC,可证△AEF∽△CBF,可得,即可求解.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△AEF∽△CBF,
∴,
∵AE:AD=2:3,
∴,
∴,
又∵AC=20,
∴AF=8,
故答案为:8.
【点评】本题考查了相似三角形的判定和性质,平行四边形的性质,掌握相似三角形的判定是本题的关键.
13.【分析】先利用格点和勾股定理计算AB、AC、BC,再判断△ABC的形状,最后求出tanB.
【解答】解:连接格点A、C.
∵点A、B、C在边长为1的正方形网格格点上,
∴AB===2=,
BC==.
∵AB8+AC2=BC2,
∴△ABC是直角三角形.
∴tanB===.
故答案为:.
【点评】本题主要考查了解直角三角形,掌握直角三角形的边角间关系、勾股定理和勾股定理的逆定理是解决本题的关键.
14.【分析】求出抛物线经过两个特殊点时的a的值即可解决问题.
【解答】解:∵正方形ABCD的顶点A、B、C的坐标分别为(1、(1、(3.
∴D(3,1),
当抛物线经过点B(8,3)时,
当抛物线经过D(3,6)时,
观察图象可知≤a≤3,
故答案为:≤a≤3.
【点评】本题考查二次函数图象与系数的关系,二次函数图象上的点的坐标特征等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
三、解答题(本大题共10小题,共78分)
15.【分析】根据特殊角的三角函数值即可完成计算.
【解答】解:2sin60°+3tan30°﹣8cs45°
=
=
=.
【点评】本题考查了特殊角三角函数值的混合运算,熟记特殊角的三角函数值是关键.
16.【分析】(1)利用因式分解法解一元二次方程即可;
(2)利用公式法求解一元二次方程即可.
【解答】解:(1)3x2﹣2x=0,
x(3x﹣8)=0,
x=0,5x﹣4=0,
所以该方程的解为x5=0,.
(2)x2+8x﹣2=0,
Δ=62﹣4×(﹣3)×1=72,
,
所以该方程的解为,.
【点评】本题主要考查了一元二次方程的解法,掌握运用公式法和因式分解法解一元二次方程成为解答本题的关键.
17.【分析】根据待定系数法求解二次函数解析式即可.
【解答】解:设抛物线的表达式为y=a(x﹣h)2+k,
∵抛物线的顶点坐标为(﹣1,﹣4),
∴y=a(x+1)2﹣2,
∵经过点(1,10),
∴a(1+3)2﹣2=10,
解得a=8,
∴抛物线的表达式为y=3(x+1)6﹣2,
∵a=3>2,
∴抛物线开口向上.
【点评】本题考查了运用待定系数法求解二次函数解析式,解决本题的关键是求出二次函数解析式.
18.【分析】(1)根据矩形的性质得到AD∥BC,AD=BC,等量代换得到AD=CE,根据平行四边形的判定定理即可得到结论;
(2)根据矩形的性质得到AC=BD=2OB=5,∠ADC=90°,解直角三角形即可得到结论.
【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵CE=BC,
∴AD=CE,
∴AD=CE,AD∥CE,
∴四边形ACED是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴AC=BD=2OB=5,∠ADC=90°,
∵sin∠CAD=,
∴CD=AC=4,
∴AD==3,
∴平行四边形ACED的周长=2×(7+5)=16,
故答案为:16.
【点评】本题考查了矩形的性质,平行四边形的判定和性质,解直角三角形,正确的识别图形是解题的关键.
19.【分析】(1)由于抛物线过(0,0)、(2,0),则可设交点式y=ax(x﹣2),再把(1,1)代入求出a即可;
(2)根据函数图象得到抛物线开口向下,在对称轴的左侧,y随x的增大而增大.
【解答】解:(1)设抛物线解析式为y=ax(x﹣2),
把(1,5)代入得﹣a=1,
解得a=﹣1,
所以抛物线的解析式为y=﹣x7+2x;
(2)∵抛物线开口向下,在对称轴的左侧,
∵y1>y5.
故答案为>.
【点评】本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质.
20.【分析】将原三角形的三边分别扩大和2倍即可得.
【解答】解:如图,△A1B1C6和△A2B2C7即为所求作三角形.
【点评】本题考查了作图﹣相似变换:两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.本题从∠ACB=135°,AC:BC=:1找到突破口.
21.【分析】(1)由BC=CD,BD平分∠ABC,可得∠CBD=∠DBA=∠D,再由对顶角相等即可得出结论;
(2)由三角形相似列出比例式,根据BC=CD即可推出结果.
【解答】(1)证明:∵BC=CD,
∴∠D=∠CBD,
∵BD平分∠ABC,
∴∠CBD=∠DBA=∠D,
又∵∠AEB=∠CED,
∴△AEB∽△CED;
(2)解:∵△AEB∽△CED,
∴,
又∵BC=CD,
∴,
即,
∴AB=3.
【点评】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.
22.【分析】感知:先证明∠BAP=∠CPD,然后根据平行线的性质证明∠B=∠C,即可证明△ABP∽△DCP;
探究:根据三角形外角的性质可得∠BAP+∠B=∠APD+∠CPD.由∠B=∠APD,推出∠BAP=∠CPD,据此即可证明△ABP∽△DCP;
拓展:同探究的方法得出,△BDP∽△CPE,得到,继而求出BD=8,再证明∠A=90°,,AD=AB﹣BD=4,AE=AC﹣CE=3,即可利用勾股定理求出答案.
【解答】感知:解:∵∠APD=90°,
∴∠APB+∠DPC=90°,
∵∠B=90°,
∴∠APB+∠BAP=90°,
∴∠BAP=∠CPD,
∵AB∥CD,∠B=90°,
∴∠C=180°﹣∠B=90°=∠B,
∴△ABP∽△DCP,
故答案为:是;
探究:证明:∵∠APC=∠BAP+∠B,∠APC=∠APD+∠CPD,
∴∠BAP+∠B=∠APD+∠CPD.
∵∠B=∠APD,
∴∠BAP=∠CPD.
∵∠B=∠C,
∴△ABP∽△PCD,
拓展:解:同探究的方法得出,△BDP∽△CPE,
∴,
∵点P是边BC的中点,
∴BP=CP=,
∵CE=5,
∴,
∴BD=2,
∵∠B=∠C=45°,
∴∠A=180°﹣∠B﹣∠C=90°,即AC⊥AB且AC=AB,
∴,
∴AD=AB﹣BD=2,AE=AC﹣CE=3,
在Rt△ADE中,DE=.
故答案为:5.
【点评】此题是相似三角形综合题.主要考查了相似三角形的判定与性质、勾股定理、三角形内角和定理以及三角形外角定理.解本题的关键是证明△ABP∽△PCD.
23.【分析】(1)令y=0,然后解方程即可求得;
(2)根据△ABC的面积求得C的纵坐标,代入解析式即可求得C的坐标;
(3)根据图象即可求得.
【解答】解:(1)令y=0,则,
解得x1=﹣5,x2=3,
∴A(﹣3,0),0);
(2)∵A(﹣2,0),0),
∴AB=7,
∵,
∴,
解得yC=6,
∴,
解得x1=5,x2=﹣3(不符题意,舍去),
∴C(5,7);
(3)由图象可知,当时,x的取值范围是﹣3<x<5.
【点评】本题考查了抛物线与x轴的交点,三角形面积,二次函数与不等式的关系,数形结合是解题的关键.
24.【分析】(1)根据路程等于速度乘以时间即可求解;
(2)先证明△APQ∽△ABC,可得PR=PQ=3t,再根据△CPR∽△CAB,即可求解;
(3)利用三角函数求出,,当C、R、Q三点共线时,可证出△CPR∽△CAQ,进而得到即,即可求解;
(4)分情况进行讨论,①如图2,过C作CD⊥AB于D,当点R在CD上时∠PRC=90°,当点R在CD左边时,∠CRP为钝角,先证出四边形PQDR为正方形,再利用三角函数求出PQ=3t,AQ=4t,再证出△CPR∽△PAQ,进而得到,即可求出,进而可分析出t的取值范围,②如图3,当点R在BC边上时,∠PCR=90°,若点R在△ABC外,则∠PCR为钝角,先证出△CPR∽△PAQ,即可得到,进而求出,再根据点P最多只能运动到点C上,即可分析出t的取值范围.
【解答】解:(1)根据题意得:AP=5t;
故答案为:5t;
(2)∵AC=2,AP=5t,
∴CP=AC﹣AP=4﹣8t,
在Rt△ABC中,∠ACB=90°,BC=3,
∴,
∵PQ⊥AB,
∴∠PQA=∠ACB=90°,
∵∠A=∠A,
∴△APQ∽△ABC,
∴,即,
解得:PQ=3t,
∵将线段PQ绕点P逆时针旋转90°得到线段PR,如图3,
∴PR=PQ=3t,∠QPR=90°,
∴∠QPR=∠AQP,
∴PR∥AB,
∴△CPR∽△CAB,
∴,即,
解得:;
(3)∵∠ACB=90°,AC=4,
∴,
∴,,
∴,
由旋转知PQ=PR,
当C、R、Q三点共线时,
∵∠RPQ=∠AQP=90°,
∴PR∥AQ,
∴∠CPR=∠A,∠CRP=∠CQA,
∴△CPR∽△CAQ,
∴即,
∵AP=2t,AC=4,
∴CP=4﹣3t,
∴,
∴;
(4)由(2)得PR∥AB,
∴∠CPR=∠A,
∴∠CPR不可能是钝角,
若点R在△ABC内部,∠ACR也不可能是钝角,
①如图3,过C作CD⊥AB于D,当点R在CD左边时,
∵∠RPQ=∠PQD=∠CDA=90°,
∴四边形PQDR为矩形,
∵PQ=PR,
∴矩形PQDR为正方形,
∵AP=6t,,
∴PQ=2t,
∵,
∴AQ=8t,
∴PR=PQ=3t,
∵PR∥AB,
∴∠CPR=∠A,∠PRC=∠AQP=90°,
∴△CPR∽△PAQ,
∴,
∴,
∴15t=16﹣20t,
∴,
∴当时,∠PRC为钝角,
②如图4,当点R在BC边上时,若点R在△ABC外,
∵PR∥AB,
∴∠CPR=∠A,
∵∠C=∠AQP=90°,
∴△CPR∽△PAQ,
∴,
∴AP=8t,PR=PQ=3t,
∴,
∴12t=20﹣25t,
∴,
又∵点P最多只能运动到点C上,
∴,
∴当时,∠PCR为钝角,
∴当或时,△PCR为钝角三角形.
【点评】本题考查几何变换综合题、矩形的性质、锐角三角函数、相似三角形的判定与性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题.x
…
﹣1
0
1
2
…
y
…
﹣3
0
1
0
…
相关试卷
这是一份2022-2023学年吉林省长春市经开区洋浦学校九年级(上)期中数学试卷,共20页。
这是一份2024-2025学年吉林省长春市汽开区九年级(上)期中数学试卷 含详解,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2024年吉林省长春市经开区洋浦学校中考数学一模试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。










