华东师大版（2024）第4章 相交线和平行线4.2 平行线2. 平行线的判定说课ppt课件

这是一份华东师大版（2024）第4章 相交线和平行线4.2 平行线2. 平行线的判定说课ppt课件，共23页。PPT课件主要包含了平行线的定义，应用格式如下，平行线的判定方法，试一试，∠130°，平行线的判定等内容，欢迎下载使用。
1.掌握平行线的三种判定方法，会运用判定方法来判断两条直线是否平行.2.能够根据平行线的判定方法进行简单的推理.
在同一平面内不相交的两条直线叫作平行线.
2.平行线的基本事实及其推论：
（1）过直线外一点有且只有一条直线与这条直线平行.
（2）如果两条直线都平行于第三条直线，那么这两条直线也互相平行.
要判断两条直线互相平行，我们无法依据它的定义，判断这两条直线在无限延长的过程中是否永远不相交.那么从上一课时画平行线的过程，我们可以得到什么启示呢？
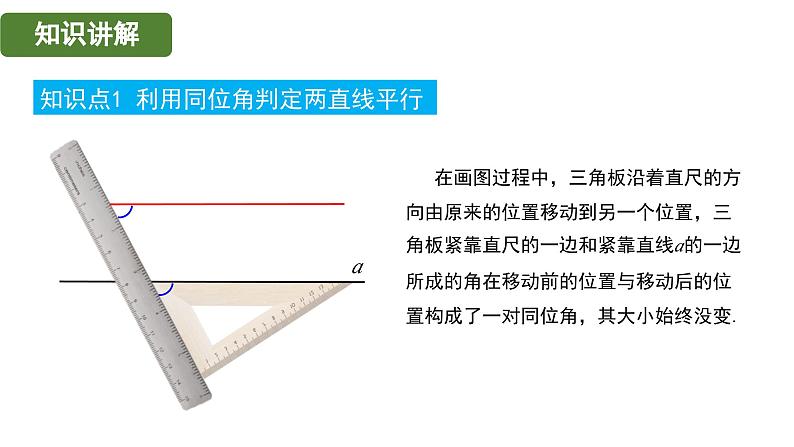
知识点1 利用同位角判定两直线平行
在画图过程中，三角板沿着直尺的方向由原来的位置移动到另一个位置，三角板紧靠直尺的一边和紧靠直线a的一边所成的角在移动前的位置与移动后的位置构成了一对同位角，其大小始终没变.
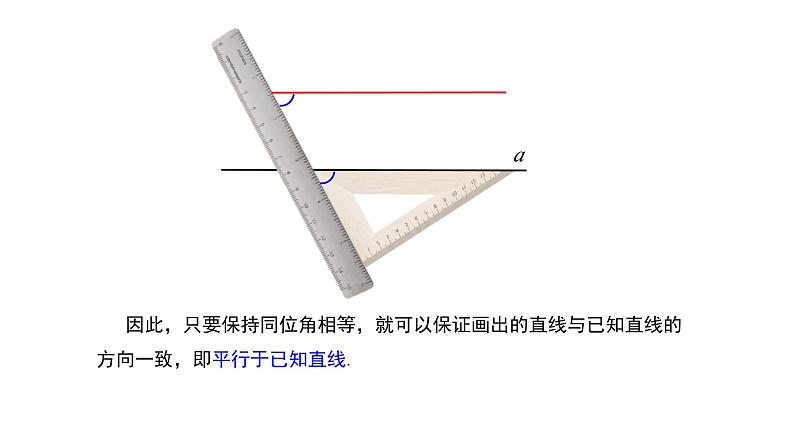
因此，只要保持同位角相等，就可以保证画出的直线与已知直线的方向一致，即平行于已知直线.
两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.简写成：同位角相等，两直线平行.
如图，∵∠1＝∠2(已知)，∴a∥b(同位角相等，两直线平行)．
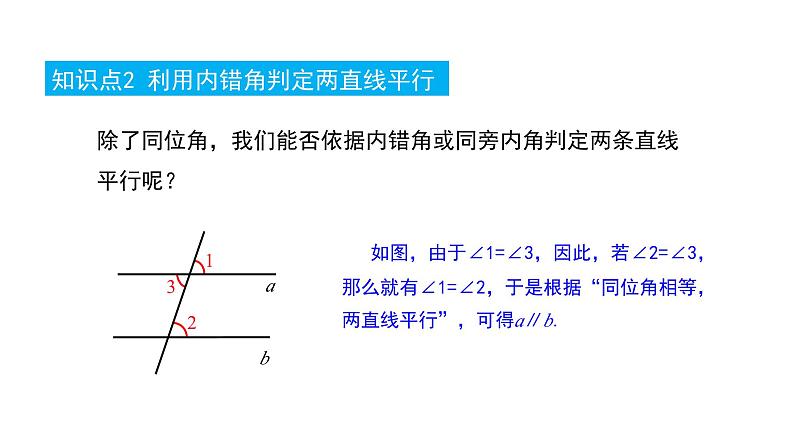
知识点2 利用内错角判定两直线平行
除了同位角，我们能否依据内错角或同旁内角判定两条直线平行呢？
如图，由于∠1=∠3，因此，若∠2=∠3，那么就有∠1=∠2，于是根据“同位角相等，两直线平行”，可得a∥b.
两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.简写成：内错角相等，两直线平行.
如图，∵∠3＝∠2(已知)，∴a∥b(内错角相等，两直线平行)．
知识点3 利用同旁内角判定两直线平行
如图，∠2和∠4为一组同旁内角，请猜想它们满足怎样的数量关系时a∥b，并说明理由.
∠2+∠4=180°时，a∥b.
理由：∵∠1+∠4=180°，∠2+∠4=180°（已知），∴∠1=∠2（同角的补角相等），∴a∥b（同位角相等，两直线平行）.
两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.简写成：同旁内角互补，两直线平行.
如图，∵∠2+∠4=180°(已知)，∴a∥b(同旁内角互补，两直线平行)．
1.同位角相等，两直线平行.2.内错角相等，两直线平行.3.同旁内角互补，两直线平行.
由平行线的判定方法，你能发现利用尺规作图过已知直线外一点作该直线的平行线的方法吗？
如图，已知直线AB，以及直线AB外一点P，试利用尺规作图过点P作直线AB的平行线.
（1）在直线AB上取一点Q，经过点P和点Q，作直线MN；
（2）作∠MPD=∠PQB，并使得∠MPD与∠PQB是一对同位角；
（3）反向延长射线PD，得到直线CD.
直线CD就是过点P所要求作的直线AB的平行线.
在同一平面内，两条直线垂直于同一条直线，这两条直线平行吗？为什么？
平行.理由：如图，∵ b⊥a，c⊥a，∴∠1=∠2=90°，∴b∥c(同位角相等，两直线平行).
在同一平面内，垂直于同一条直线的两条直线平行.
1.如图，下列四个图中，∠1=∠2，不能判定a∥b的是（ ）
2. 如图，下列推理错误的是(　　)A．若∠1＝∠2，则c∥d B．若∠3＝∠4，则c∥dC．若∠1＝∠3，则a∥b D．若∠1＝∠4，则a∥b
3. 如图，下列能判定AC∥DF的条件有(　　)①∠1+∠DEC=180°；②∠C=∠2；③∠4=∠FEC；④∠DEF=∠5；⑤∠3=∠4.A.1个B.2个C.3个D.4个
4. 如图，点E是AD延长线上一点，∠B=30°，∠C=120°.如果添加一个条件，使BC∥AD，则可添加的条件为__________.(只填一个即可)
5. 如图，已知∠1= ∠3，AC平分∠DAB，你能判断哪两条直线平行？请说明理由？
解：AB∥CD，理由：AC平分∠DAB，所以∠1=∠2，因为∠1=∠3，所以∠2=∠3，所以AB∥CD.（内错角相等，两直线平行）
6.如图，已知∠B=25°，∠BCD=45°，∠CDE=30°，∠E=10°.试说明：AB∥EF.
解：在∠BCD的内部作∠BCM=25°，在∠CDE的内部作∠EDN=10°.∵∠B=25°，∠E=10°，∴∠B=∠BCM，∠E=∠EDN，∴AB∥CM，EF∥DN.
又∵∠BCD=45°，∴∠MCD=∠BCD-∠BCM=45°-25°=20°.同理可得∠CDN=20°，∴∠MCD=∠CDN，∴CM∥DN.又∵AB∥CM，EF∥DN，∴AB∥EF.
a.同位角相等,两直线平行. b.内错角相等,两直线平行.c.同旁内角互补，两直线平行.