





数学七年级上册(2024)2. 平行线的判定教案配套课件ppt
展开掌握平行线的三种判定方法,会运用判定方法来判 断两条直线是否平行;
能够根据平行线的判定方法进行简单的推理.
问题1 两条不重合的直线的位置关系有哪几种?
问题2 怎样的两条直线平行?
问题3 上节课我们学了平行线的哪些内容?
相交(包括垂直)和平行两种.
在同一平面内,不相交的两条直线平行.
2.如果两条直线都与第三条直线平行,那么这两条直线互相平行.
1.经过直线外一点,有且只有一条直线与已知直线平行.
根据平行线的定义,如果同一平面内的两条直线不相交,就可以判断这两条直线平行.
由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否相交来判定是否平行,那么有没有其他判定方法呢?
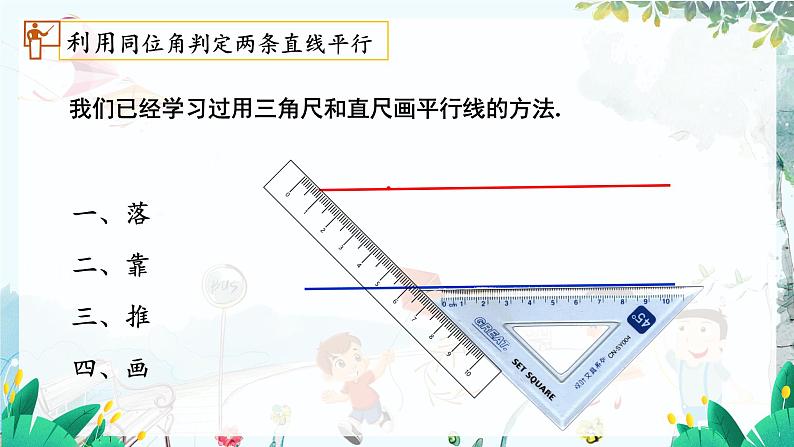
我们已经学习过用三角尺和直尺画平行线的方法.
利用同位角判定两条直线平行
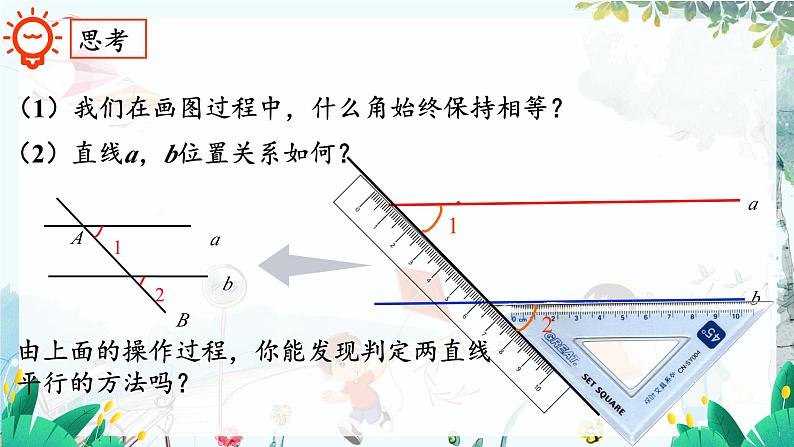
(1)我们在画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
由上面的操作过程,你能发现判定两直线平行的方法吗?
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简写成:同位角相等,两直线平行.
因为∠1=∠2(已知),所以l1∥ l2(同位角相等,两直线平行).
(1) 图中若∠1=55°,∠2=55°直线AB与CD平行吗?为什么?
所以AB//CD.(同位角相等,两直线平行)
因为∠1=∠2=55°(已知)
(2)如图,∠1=55°,∠2=125°,直线AB与CD平行吗?为什么?
所以AB与CD (同位角相等,两直线平行)
因为∠2=125°(已知)
所以∠ANF=180°-∠2=55°
所以∠ ANF = ∠1
除了同位角,我们能否依据内错角或同旁内角判定两直线平行呢?
如图,由∠3=∠2,可推出a//b吗?如何推出?
所以 a//b(同位角相等,两直线平行).
利用内错角、同旁内角判定两条直线平行
解: 因为 ∠ 3= ∠ 2(已知), ∠ 1= ∠ 3(对顶角相等),
所以 ∠ 1= ∠ 2(等量代换)
两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简写成:内错角相等,两直线平行.
如图,由∠1+∠2=180°,你能判定a//b吗?
因为 ∠1+∠2=180°(已知) ∠1+∠3=180°(邻补角定义)
所以 ∠2=∠3(同角的补角相等)
所以 a∥ b(同位角相等,两直线平行)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简写:同旁内角互补,两直线平行.
平行线的判定方法:1.同位角相等,两直线平行;2.内错角相等,两直线平行3.同旁内角互补,两直线平行。
我们已经知道利用尺规作图可以作一条线段等于已知线段,以及作一个角等于已知角的方法.那么,如何过已知直线外一点作该直线的平行线呢?由平行线的判定方法,你自然会想到在直线AB和直线外一点P处,设法如图那样构造一对相等的同位角∠1和∠ 2,那样就可以作出所需要的平行线了.由此,你能发现利用尺规作图过已知直线外一点作该直线的平行线的方法吗?
如图,已知直线AB,以及直线AB外一点P, 试利用尺规作图按下列作法准确地过点Р作直线AB的平行线: (1)在直线AB上取一点Q,经过点Р和点Q,作直线MN; (2)作∠MPD = ∠PQB,并使得∠MPD与∠PQB是一对同位角; (3)反向延长射线PD,得到直线CD . 直线CD就是过点Р所要求作的直线AB的平行线.
例1 如图,直线a、b被直线l所截,已知∠1=115°, ∠2=115° ,直线a、b平行吗?为什么?
∵ ∠1=115°(已知) ∠2=115°(已知)
∴ ∠1=∠2(等量代换)
∴ a∥ b(内错角相等,两直线平行)
我们用符号“∵”“∴”分别表示“因为”“所以”
演绎推理是一种从一般到特殊的推理,借助于一些公认的基本事实及由此推导得出结论,通过判断,说明最后结论的正确.
例2 如图,在四边形ABCD中,已知∠B=60°,∠C=120°, AB与CD平行吗?AD与BC平行吗?
∵ ∠B=60°(已知) ∠C=120°(已知)
∴ ∠B+∠C=180°(已知)
∴ AB∥ CD(同旁内角互补,两直线平行)
根据已知条件,无法判定AD与BC是否平行.
例3 如图,在同一平面内,直线CD、EF均与直线AB垂直,点D、F为垂足,试判断CD与EF是否平行.
解: ∵CD⊥AB(已知) ,EF⊥AB(已知), ∴∠ADC=∠AFE=90°. ∴CD∥ EF(同位角相等,两直线平行)
同一平面内,垂直于同一条直线的两条直线平行.
1.根据题图,在下列解答中,填上适当的理由:【教材P188 练习 第1题】
∴AB∥CD( )
(1)∵∠B=∠1(已知)
(2)∵∠D =∠1(已知)
∴ AD∥ BC( )
同位角相等,两直线平行
内错角相等,两直线平行
2.根据题图,在下列解答中,填空: 【教材P188 练习 第2题】(1)∵∠BAD+∠ABC=180°(已知) ∴( )∥( )(同旁内角互补,两直线平行)(2)∵∠BCD+∠ABC=180°(已知) ∴( )∥( )(同旁内角互补,两直线平行)
3.根据图中给出的条件,指出互相平行的直线和互相垂直的直线 【教材P188 练习 第3题】
解: a∥ b,c∥ d, a⊥e,b⊥e
4.如图,已知∠1=∠3, AC平分∠DAB,你能判断哪两条直线平行?请说明理由?
∴ CD∥AB(内错角相等,两直线平行).
证明过程如下: ∵ AC平分∠DAB(已知),
∴ ∠1=∠2(角平分线定义).
又∵ ∠1= ∠3(已知),
∴ ∠2=∠3(等量代换),
判定两条直线平行的方法
初中数学华师大版七年级上册3 平行线的性质教课内容课件ppt: 这是一份初中数学华师大版七年级上册3 平行线的性质教课内容课件ppt,共10页。PPT课件主要包含了新知引入,新知巩固,例题讲解,随堂练习,ABCD等内容,欢迎下载使用。
初中数学华师大版七年级上册第2章 有理数2.2 数轴1 数轴优秀ppt课件: 这是一份初中数学华师大版七年级上册第2章 有理数2.2 数轴1 数轴优秀ppt课件,文件包含1数轴课件pptx、2在数轴上比较数的大小课件pptx、习题22课件pptx等3份课件配套教学资源,其中PPT共38页, 欢迎下载使用。
华师大版七年级上册第5章 相交线与平行线5.2 平行线2 平行线的判定教学ppt课件: 这是一份华师大版七年级上册第5章 相交线与平行线5.2 平行线2 平行线的判定教学ppt课件,共20页。PPT课件主要包含了应用格式,总结归纳,BCD,ABC,解AB∥CD,同位角,同旁内角,∠1∠2等内容,欢迎下载使用。













