（华师大版）2024-2025学年八年级数学上学期期中押题测试卷（一）

这是一份（华师大版）2024-2025学年八年级数学上学期期中押题测试卷（一），文件包含华师大版2024-2025学年八年级数学上学期期中押题测试卷一原卷版docx、华师大版2024-2025学年八年级数学上学期期中押题测试卷一解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
4．测试范围：（华师版）八年级上册 第一章~第三章。
5．难度系数：0.85。
一、选择题（本题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题目要求的。）
1．425的平方根是（ ）
A．25B．16625C．±25D．±16625
【答案】C
【分析】根据平方根的定义，求数a的平方根，也就是求一个数x，使得x2=a，则x就是a的平方根，由此即可解决问题．
【详解】∵(±25)2=425，
∴425的平方根是±25
故选C.
【点睛】此题考查平方根，解题关键在于掌握运算法则
2．一个等腰三角形的两条边长分别3和6，则该等腰三角形的周长是（ ）
A．12B．13C．15D．12或15
【答案】C
【分析】根据等腰三角形的定义，分两种情况：①腰长为3，底边长为6；②腰长为6，底边长为3，然后结合三角形的三边关系验证是否都成立，最终求出满足题意的三角形的周长．
【详解】解：∵一个等腰三角形的两条边长分别3和6，
∴由等腰三角形的性质，分两种情况讨论：①腰长为3，底边长为6；②腰长为6，底边长为3，
当腰长为3，底边长为6时， 由于3+3=6，结合三角形三边关系可知此情况的3条边长无法构成三角形，故该三角形不存在；
当腰长为6，底边长为3时，3条边长可以构成三角形，故该等腰三角形的周长是6+6+3=15；
综上所述，该等腰三角形的周长是15，
故选：C．
【点睛】本题考查等腰三角形的定义及三角形三边关系判定已知三边是否构成三角形，熟练把握等边三角形有两条边相等进行分类讨论是解决问题的关键．
3．如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（ ）
A．△ABC的三条中线的交点
B．△ABC三条角平分线的交点
C．△ABC三条高所在直线的交点
D．△ABC三边的中垂线的交点
【答案】B
【分析】本题考查的是角平分线的性质．根据角平分线的性质“角的平分线上的点到角的两边的距离相等”解答即可．
【详解】解：∵三角形角平分线上的点到角两边的距离相等，
∴凉亭的位置应选在三角形三条角平分线的交点上．
故：B．
4．如图，每个小正方形的边长都是1，A，B，C分别在格点上，则∠ABC的度数为（ ）.
A．30°B．45°C．50°D．60°
【答案】B
【分析】连接AC，根据勾股定理逆定理可得△ABC是以AC、BC为腰的等腰直角三角形，据此可得答案．
【详解】解：如图，连AC，
则BC=AC=12+22=5，AB=32+12=10，
∵(5)2+(5)2=(10)2，
即BC2+AC2=AB2，
∴△ABC为等腰直角三角形，∠ACB=90°，
∴∠ABC=45°．
故选：B．
【点睛】本题考查了勾股定理及其逆定理，解题的关键是掌握勾股定理及其逆定理和等腰直角三角形的判定和性质．
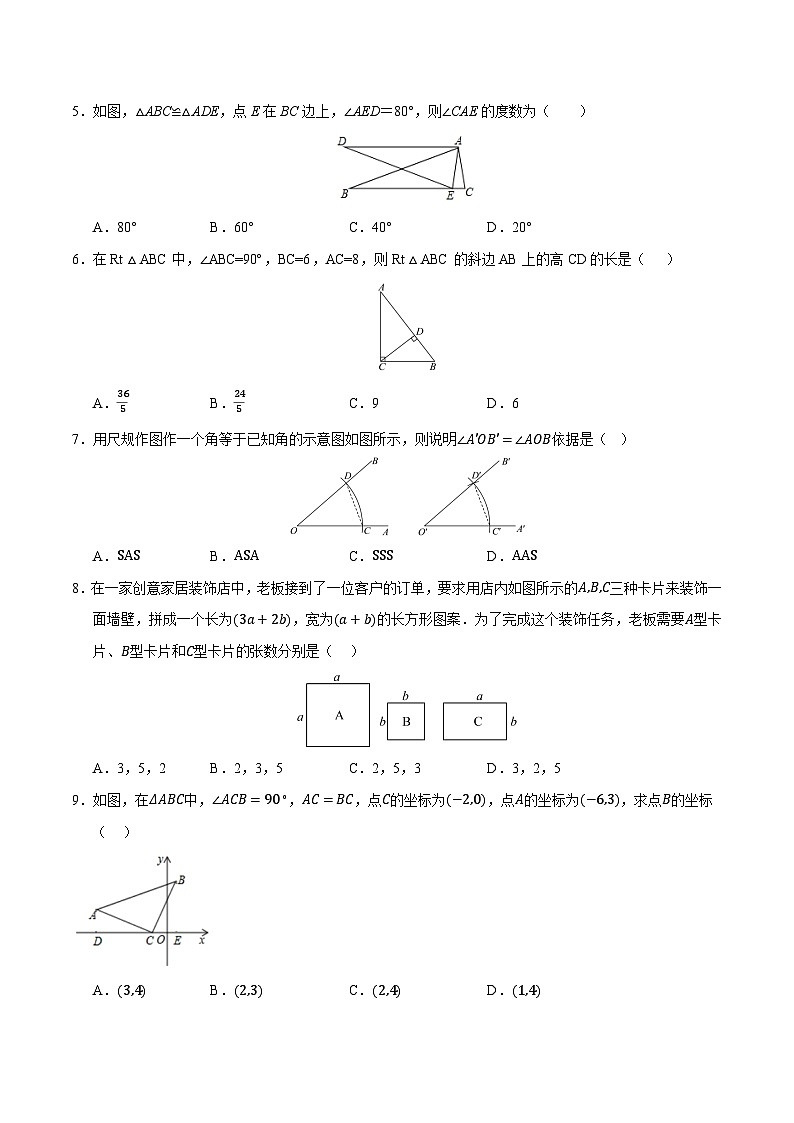
5．如图，△ABC≌△ADE，点E在BC边上，∠AED＝80°，则∠CAE的度数为（ ）
A．80°B．60°C．40°D．20°
【答案】D
【分析】根据全等三角形的性质得出∠C=∠AED=80°，AE=AC，根据等腰三角形的性质得出∠AEC=∠C=80°，根据三角形内角和定理求出即可．
【详解】解：∵△ABC≌△ADE，∠AED＝80°，
∴∠C＝∠AED＝80°，AE＝AC，
∴∠AEC＝∠C＝80°，
∴∠CAE＝180°﹣∠C﹣∠AEC＝180°﹣80°﹣80°＝20°，
故选D．
【点睛】本题考查了全等三角形的性质，等腰三角形的性质和三角形的内角和定理，能熟记全等三角形的性质定理的内容是解此题的关键，注意：全等三角形的对应边相等，对应角相等．
6．在Rt△ABC中，∠ABC=90º，BC=6，AC=8，则Rt△ABC的斜边AB上的高CD的长是（ ）
A．365B．245C．9D．6
【答案】B
【分析】先由勾股定理算出AB=10，然后再由Rt△ABC中等面积法得到12AC×BC=12AB×CD即可求解．
【详解】解：由勾股定理有：AB=AC2+BC2=82+62=10，
在Rt△ABC中，由等面积法可知：12AC×BC=12AB×CD，
代入数据：8×6=10×CD，
解得：CD=245，
故选：B．
【点睛】本题考查了勾股定理、直角三角形面积的计算方法；熟练掌握勾股定理，运用直角三角形面积的计算方法求出CD是解决问题的关键．
7．用尺规作图作一个角等于已知角的示意图如图所示，则说明∠A′OB′=∠AOB依据是（ ）
A．SASB．ASAC．SSSD．AAS
【答案】C
【分析】本题考查了作图-基本作图：作一个角等于已知角．利用基本作图得到OD=OC=O′D′=O′C′，CD=C′D′，则根据全等三角形的判定方法可根据“SSS”可判断△OCD≌△O′C′D′，然后根据全等三角形的性质得到∠A′OB′=∠AOB．
【详解】由作法可得OD=OC=O′D′=O′C′，CD=C′D′，
所以根据“SSS”可判断△OCD≌△O′C′D′，
所以∠A′OB′=∠AOB．
故选：C．
8．在一家创意家居装饰店中，老板接到了一位客户的订单，要求用店内如图所示的A,B,C三种卡片来装饰一面墙壁，拼成一个长为3a+2b，宽为a+b的长方形图案．为了完成这个装饰任务，老板需要A型卡片、B型卡片和C型卡片的张数分别是（ ）
A．3，5，2B．2，3，5C．2，5，3D．3，2，5
【答案】D
【分析】本题主要考查了多项式的乘法的应用，熟练掌握多项式乘以多项式法则是解题关键．根据长方形的面积公式可知该墙壁面积S=3a2+2b2+5ab，即可得出答案．
【详解】解：∵ 长方形的长为3a+2b，宽为a+b，
∴长方形的面积S=3a+2ba+b=3a2+2b2+5ab，
∴需要A型卡片、B型卡片和C型卡片的张数分别3、2、5张．
故选：D．
9．如图，在ΔABC中，∠ACB=90∘，AC=BC，点C的坐标为(−2,0)，点A的坐标为(−6,3)，求点B的坐标（ ）
A．3,4B．2,3C．2,4D．1,4
【答案】D
【分析】由题意过A和B分别作AD⊥OC于D，BE⊥OC于E，利用已知条件可证明△ADC≌△CEB，再由全等三角形的性质和已知数据即可求出B点的坐标．
【详解】解：过A和B分别作AD⊥OC于D，BE⊥OC于E，
∵∠ACB=90°，
∴∠ACD+∠CAD=90°∠ACD+∠BCE=90°，
∴∠CAD=∠BCE，
在△ADC和△CEB中，
∠ADC＝∠CBE＝90°∠CAD＝∠BCEAC＝BC
∴△ADC≌△CEB（AAS），
∴DC=BE，AD=CE，
∵点C的坐标为（-2，0），点A的坐标为（-6，3），
∴OC=2，AD=CE=3，OD=6，
∴CD=OD-OC=4，OE=CE-OC=3-2=1，
∴BE=4，
∴则B点的坐标是（1，4）．
故选：D.
【点睛】本题考查等腰直角三角形的性质、全等三角形的性质和判定、坐标与图形特点，本题能根据AAS证明两三角形全等是关键，利用坐标与图形特点根据坐标写出线段的长，反之，能根据线段的长写出B的坐标，注意象限的符号问题．
10．如图，等边三角形ABD与等边三角形ACE，连接BE、CD，BE的延长线与CD交于点F，连接AF，有以下四个结论：①BE=CD；②FA平分∠EFC；③∠BFC=120°；④EF=DF；⑤FA−FC=FE．其中一定正确的结论是（ ）

A．①②③④⑤B．①②③④C．①②③⑤D．①②④⑤
【答案】C
【分析】①根据等边三角形的性质证出△BAE≅△DAC，可得BE=CD，从而得出①正确；
②过A作AM⊥BF于M，过A作AN⊥DC于N，由△BAE≅△DAC得出∠BEA=∠ACD，由等角的补角相等得出∠AEM=∠CAN，由AAS可证△AME≅△ANC，得到AM=AN，由角平分线的判定定理得到FA平分∠EFC，从而得出②正确；
③在FA上截取FG，使FG=FE，求出∠EFC=120∘即可得出∠BFD=60∘，得出③正确；
④根据CF+EF＝AF，CF+DF＝CD，得出CD≠AF，从而得出FE≠FD，即可得出④错误；
⑤根据全等三角形的判定与性质得出△AGE≅△CFE，可得AG=CF，即可求得AF=CF+EF，从而得出⑤正确．
【详解】①解：∵△ABD和△ACE是等边三角形，
∴∠BAD=∠EAC=60∘，AE=AC=EC
∵∠BAE+∠DAE=60∘，∠CAD+∠DAE=60∘
∴∠BAE=∠DAC
在△BAE和△DAC中
∵AB=AD∠BAE=∠DACAE=AC
∴△BAE≅△DAC(SAS)
∴BE=CD，①正确；
②解：过A作AM⊥BF于M，延长DC，过A作AN⊥DC于N，如图1.
∵△BAE≅△DAC
∴∠BEA=∠ACD
∠AEM=∠ACN
∵AM⊥BF，AN⊥DC
∴∠AME=∠ANC=90∘
在△AME和△ANC中：
∵∠AEM=∠CAN∠AME=∠ANCAE=AC
∴△AME≅△ANC
∴AM=AN
∵AM⊥BF，AN⊥DC，AM=AN
∴FA平分∠EFC，②正确；

③解：在FA上截取FG，使FG=FE，如图2，
∵∠BEA=∠ACD，∠BEA+∠AEF=180∘
∴∠AEF+∠ACD=180∘
∠EAC+∠EFC=180∘
∵∠EAC=60∘
∴∠BFC=∠EFC=120°，③正确；

⑤解：∵FA 平分∠EFC
∴∠EFA=∠CFA=60∘
∵EF=FG，∠EFA=60∘
∴△EFG是等边三角形，
EF=EG
∵∠AEG+∠CEG=60∘，∠CEG+∠CEF=60∘
∴∠AEG=∠CEF
在△AGE和△CFE中，
∵AE=AC∠AEG=∠CEFEG=EF
∴△AGE≅△CFE(SAS)
∴AG=CF
∵AF=AG+FG
∴AF=CF+EF
FA−FC=EF，⑤正确；
④解：∵FA−FC=EF，CF+DF=CD
CD≠AF
∴FE≠FD，④错误.
故选：C.
【点睛】本题主要考查了等边三角形的判定与性质以及全等三角形的判定与性质，正确作辅助线，构造全等三角形，是解答本题的关键．
填空题（本题共6小题，每小题3分，共18分．）
11．−3的相反数是 ．
【答案】3
【分析】仅仅只有符号不同的两个数互为相反数，根据相反数的定义直接可得答案．
【详解】解：−3的相反数是3,
故答案为：3
【点睛】本题考查的是相反数的含义，掌握“相反数的含义”是解本题的关键．
12．若30.00375=0.1554，3a=15.54，则a= ．
【答案】3750
【分析】本题考查被开方数和立方根之间的小数点位数的移动关系．根据被开方数和立方根之间的小数点位数的移动关系，进行计算即可．
【详解】解：∵30.00375=0.1554，3a=15.54，
∴a=3750．
故答案为：3750．
13．因式分解∶ a3−9a= ．
【答案】aa+3a−3
【分析】本题考查了因式分解，先提公因式，再利用平方差公式分解即可．
【详解】解：a3−9a
=aa2−9
=aa+3a−3，
故答案为：aa+3a−3．
14．如图，射线OC是∠AOB的角平分线，D是射线OC上一点，DP⊥OA于点P，DP=5，若点Q是射线OB上一点，OQ=4，则△ODQ的面积是 ．

【答案】10
【分析】作DH⊥OB于点H，根据角平分线的性质得到DH=DP=5，根据三角形的面积公式计算，得到答案．
【详解】解：作DH⊥OB于点H，如图所示：
∵ OC是∠AOB的角平分线，DP⊥OA，DH⊥OB，
∴ DH=DP=5，
∴S△ODQ=12×OQ×DH=12×4×5=10,
故答案为：10
【点睛】本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
15．若x2−kx+9是一个完全平方式，则k= ．
【答案】±6
【分析】本题主要考查了完全平方式，根据平方项确定出这两个数是解题的关键，也是难点，熟记完全平方公式对解题非常重要．
根据已知可得完全平方式是x±32=x2±6x+9，依据对应相等可得−kx=±6x，解得k=±6．
【详解】解：x2−kx+9=x2−kx+32．
∵x2−kx+9是一个完全平方式，
∴−kx=±6x
∴−kx=±6x．
∴k=±6．
故答案为：±6．
16．如图，做一个“U”字形框架PABQ，其中AB=42cm，AP、BQ足够长，PA⊥AB，QB⊥AB，点M从点B出发，向点A运动，同时点N从点B出发，向点Q运动，点M、N运动的速度之比为3：4，当M、N两点运动到某一瞬间同时停止，此时在射线AP上取点C，使△ACM与△BMN全等，则此时线段AC= cm．

【答案】18或28
【分析】本题主要考查了全等三角形的性质，设BM=3tcm，则BN=4tcm，使△ACM与△BMN全等，由∠A=∠B=90°可知，分两种情况：情况一：当BM=AC，BN=AM时，列方程解得t，可得AC；情况二：当BM=AM，BN=AC时，列方程解得t，可得AC．
【详解】解：设BM=3tcm，则BN=4tcm，
∵∠A=∠B=90°，使△ACM与△BMN全等，分两种情况：
情况一：当BM=AC，BN=AM时，
∵BN=AM，AB=42cm，
∴4t=42−3t，
解得：t=6，
∴AC=BM=3t=3×6=18cm，
情况二：当BM=AM，BN=AC时，
∵BM=AM，AB=42cm，
∴3t=42−3t，
解得：t=7，
∴AC=BN=4t=4×7=28cm，
故答案为：18或28．
三．解答题（本题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤．）
17．（4分）计算 −5+16−32+3−8
【答案】−2
【分析】根据求绝对值，算术平方根，立方根进行计算即可解答．
【详解】解：−5+16−32+3−8
=5+4−9−2
=−2
【点睛】本题考查了实数的混合运算，熟练掌握算术平方根和立方根是解题的关键．
18．（8分）解下列方程
(1)4(x−1)2=9
(2)1125(x−3)3=−1
【答案】(1)x=52或x=−12；
(2)x=−2
【分析】此题考查了用平方根和立方根的意义解方程．
（1）变形后得到(x−1)2=94，则x−1=±32，即可求出方程的解；
（2）变形后得到(x−3)3=−125，则x−3=−5，即可求出方程的解．
【详解】（1）解：4(x−1)2=9
∴(x−1)2=94，
根据平方根的意义得到，x−1=±32，
∴x−1=32或x−1=−32，
解得x=52或x=−12；
（2）1125(x−3)3=−1
∴(x−3)3=−125，
根据立方根的意义得到，x−3=−5，
解得x=−2．
19．（8分）已知3b+3的平方根为±3，3a+2b的算术平方根为5
(1)求a，b的值；
(2)求4a−6b的平方根．
【答案】(1)a，b的值分别为7，2
(2)±4
【分析】（1）运用立方根和算术平方根的定义求解即可；
（2）先将a、b的值代入求值，然后再根据平方根的定义即可解答．
【详解】（1）解：∵3b+3的平方根为±3，
∴3b+3=9，解得b=2，
∵3a+2b的算术平方根为5，
∴3a+2b=25，即3a+2×2=25
∴a=7．
综上所述：a，b的值分别为7，2；
（2）解：∵a=7，b=2，
∴4a−6b=16，
∴4a−6b的平方根为±16，即±4．
【点睛】本题主要考查了平方根、算术平方根等知识点，平方根、算术平方根的定义求得a、b的值是解答本题的关键．
20．（8分）如图，AB=DE，AC=DF，BE=CF．求证：AB∥DE.
【答案】见解析
【分析】首先判定△ABC≌△DEF，然后利用全等三角形性质得出∠ABC=∠DEF，进而得出AB∥DE.
【详解】∵BE=CF
∴BE+EC=CF+EC
∴BC=EF
∵AB=DE，AC=DF，
∴△ABC≌△DEF（SSS）
∴∠ABC=∠DEF
∴AB∥DE.
【点睛】此题主要考查全等三角形的判定与性质以及平行的性质，熟练掌握，即可解题.
21．（10分）如图，DE⊥AB于E，DF⊥AC于F，若BD=CD、BE=CF，

(1)求证：AD平分∠BAC；
(2)已知AC=20，BE=4，求AB的长．
【答案】(1)见详解
(2)12
【分析】本题考查了全等三角形的性质和判定的应用，注意：全等三角形的判定定理有SAS,ASA,AAS,SSS，全等三角形的对应边相等，对应角相等．
（1）求出∠E=∠DFC=90°，根据全等三角形的判定定理得出Rt△BED≌Rt△CFD，推出DE=DF，根据角平分线性质得出即可；
（2）根据全等三角形的性质得出AE=AF,BE= CF，即可求出答案．
【详解】（1）证明：∵DE⊥AB,DF⊥AC，
∴∠E=∠DFC=90°，
∴在Rt△BED和Rt△CFD中，
BD=CDBE=CF，
∴Rt△BED≌Rt△CFD(HL)，
∴DE=DF，
∵DE⊥AB,DF⊥AC，
∴AD平分∠BAC；
（2）解：∵∠AED=∠AFD=90°,AD=AD,DE=DF，
∴Rt△ADE≌Rt△ADF(HL)，
∴AE=AF，
∵AC=20,CF=BE=4，
∴AE=AF=20−4=16，
∴AB=AE−BE=16−4=12．
22．（10分）阅读材料，完成下列任务：
因为无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来比如：π、2等，而常用的“…”或者“≈”的表示方法都不够百分百准确．
材料一：∵4<7<9，即2<7<3，∴1<7−1<2．
∴7−1的整数部分为1，小数部分为7−2．
材料二：我们还可以用以下方法求一个无理数的近似值．
我们知道面积是2的正方形的边长是2，易知2>1，因此可设2=1+x可画出如图示意图．
解：由图中面积计算，S正方形=x2+2×1⋅x+1，
∵S正方形=2，
∴x2+2×1⋅x+1=2．
∵x是2的小数部分，小数部分的平方很小，直接省略x2，
∴得方程2x+1=2，解得x=0.5，即2≈1.5．
解决问题：
(1)利用材料一中的方法，求85的小数部分；
(2)利用材料二中的方法，借助面积为5的正方形探究5的近似值．（画出示意图，标明数据，并写出求解过程）
【答案】(1)85−9
(2)5≈2.25，见解析
【分析】本题考查了无理数的估算，解题关键是准确理解题目给出的方法，熟练进行计算．
（1）根据材料一中的方法求解即可；
（2）利用材料二中的方法画出图形，写出过程即可．
【详解】（1）解：∵81<85<100，即9<85<10
∴85的整数部分为9．
∴85的小数部分为85−9．
（2）解：∵面积是5的正方形的边长是5， 5>2，
∴可设5=2+x
画出示意图如图所示
由图中面积计算，S正方形=x2+2×2⋅x+4，
∵S正方形=5，
∴x2+2×4⋅x+4=5
∵x是5的小数部分，小数部分的平方很小，直接省略x2，
∴得方程4x+4=5，解得x=0.25，
即5≈2.25
23．（12分）【阅读理解】“若x满足70−xx−20=30，求(70−x)2+(x−20)2的值”．
解：设70−x=a，x−20=b，
则70−xx−20=ab=30，a+b=70−x+x−20=50，
那么(70−x)2+(x−20)2=a2+b2=(a+b)2−2ab=502−2×30=2440．
【解决问题】
(1)若x满足40−xx−10=−10，求(40−x)2+(x−10)2的值；
(2)若x满足(2020−x)2+(2019−x)2=4041，求2020−x2019−x的值；
(3)如图，正方形ABCD的边长为x，AE=14，CG=20，长方形EFGD的面积是500，四边形NGDH和MEDQ都是正方形，四边形PQDH是长方形，求图中阴影部分的面积(结果必须是一个具体的数值)．
【答案】(1)920
(2)2020−x2019−x=2020；
(3)阴影部分的面积为2036．
【分析】本题考查了完全平方公式，解决本题的关键是熟记完全平方公式，进行转化应用．
（1）根据举例进行对已知式子计算解答即可；
（2）设2020−x=c，2019−x=d，则可得c2+d2=4041，c−d=1，所以2cd=c2+d2−(c−d)2=4040，可得cd=2020，即可解答；
（3）根据正方形ABCD的边长为x，AE=14，CG=20，所以DE=x−14，DG=x−20，得到x−14x−20=500，设x−14=a，x−20=b，从而得到ab=500，a−b=6，根据举例求出(a+b)2，即可求出阴影部分的面积．
【详解】（1）解：设40−x=m，x−10=n，
∴40−xx−10=mn=−10，
∴m+n=40−x+x−10=30，
∴(40−x)2+(x−10)2，
=m2+n2，
=(m+n)2−2mm，
=302−2×−10
=920；
（2）解：设2020−x=c，2019−x=d，
∴c2+d2=(2020−x)2+(2019−x)2=4041，
∴c−d=2020−x−2019−x=1，
∴2cd=c2+d2−(c−d)2=4040，
∴cd=2020，
即2020−x2019−x=2020；
（3）解：∵正方形ABCD的边长为x，AE=14，CG=20，
∴DE=x−14，DG=x−20，
∴x−14×x−20=500，
设x−14=a，x−20=b，
∴ab=500，a−b=x−14−x−20=6，
(a+b)2=(a−b)2+4ab=62+4×500=2036，
答：阴影部分的面积为2036．
24．（12分）已知，在等边三角形ABC中，点O在AB上，点P在CB的延长线上，且OP=OC．
(1)如图1，当点O为AB的中点时，确定线段AO与PB的大小关系，请你直接写出结论；
(2)如图2，当点O为AB边上任意一点，确定线段AO与PB的大小关系，请你写出结论，并说明理由；
(3)在等边三角形ABC中，点O在直线AB上，点P在直线BC上，且OP=OC，若△ABC的边长为2，AO=5，求CP的长．
【答案】(1)AO=PB
(2)相等，见解析
(3)7或3
【分析】（1）利用等腰三角形的性质，三线合一性质，等边三角形的性质，计算说明即可．
（2）过O作OQ∥BC交AC于Q，证明△AOQ是等边三角形，以及△POB≌△OCQAAS即可证明．
（3）分为点O在射线AB上或点O在射线BA上两种情况，利用全等、等腰三角形的性质即可证明．
【详解】（1）解：AO=PB，理由如下：
∵△ABC为等边三角形，点O为AB的中点，
∴∠ABC=∠ACB=60°，CO平分∠ACB，AO=BO，
∴∠OCB=12∠ACB=30°，
∵OP=OC，
∴∠P=∠OCB=30°，
∵∠ABC=∠P+∠POB，
∴∠POB=∠ABC−∠P=30°，
∴∠P=∠POB，
∴PB=BO，
∴AO=PB；
（2）解：相等，即AO=PB，理由如下：
如图，过O作OQ∥BC交AC于Q，
∵△ABC是等边三角形，
∴∠ABC=∠ACB=∠A=60°，AB=AC=BC，
∴∠AOQ=∠ABC=60°，∠AQO=∠ACB=60°，
即∠AOQ=∠AQO=∠A=60°，
∴△AOQ是等边三角形，
∴AO=AQ=OQ，
∵∠ABC=∠ACB=∠AQO=60°，
∴∠PBO=∠OQC=120°，∠P+∠BOP=∠QCO+∠OCP=60°，
∵PO=OC，
∴∠P=∠OCP，
∴∠BOP=∠OCQ，
在△POB和△OCQ中，
∠PBO=∠OQC∠POB=∠OCQPO=OC，
∴△POB≌△OCQAAS，
∴PB=OQ，
∴AO=PB．
（3）解：如图③，当点O在射线AB上时，过O作OQ∥BC交AC的延长线于Q，
则△AOQ为等边三角形，∠OCP=∠COQ，
∴AQ=AO=OQ=5，∠Q=60°，
∵PO=CO，
∴∠P=∠OCP，
∴∠COQ=∠P，
∵△ABC是等边三角形，
∴BC=AC=2，∠ABC=60°，
∴∠PBO=∠ABC=60°，
∴∠Q=∠PBO，
在△COQ和△OPB中，
∠Q=∠PBO∠COQ=∠POC=PO，
∴△POB≌△OCQAAS，
∴BP=OQ=5，
∴CP=BP+BC=2+5=7；
如图，当点O在射线BA上时，∵BA=2，AO=5，
∴OB=7，
∵△ABC是等边三角形，
∴∠B=60°，BC=BA=2，
过点O作OD⊥BP，则∠BOD=30°，
∴BD=12OB=72，
∴CD=BD−BC=72−2=32，
又∵OC=OP，
∴PC=2CD=3；
综上所述，PC长为7或3．
．
【点睛】本题考查了等腰三角形的判定和性质，等边三角形的判定和性质，三角形全等的判定和性质，三角形外角的性质，熟练掌握等边三角形的判定和性质，三角形全等的判定和性质是解题的关键．