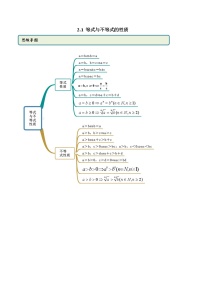
数学第二册上册不等式的性质同步训练题

这是一份数学第二册上册不等式的性质同步训练题，共11页。试卷主要包含了依据，结论，作出结论．等内容，欢迎下载使用。

一．关于实数a，b大小比较的基本事实
1.两个实数a，b，其大小关系有三种可能，即a>b，a＝b，ab⇔a－b>0；a＝b⇔a－b＝0；ac，那么a>c，即a>b，b>c⇒a>c.
性质3 如果a>b，那么a＋c>b＋c.
性质4 如果a>b，c>0，那么ac>bc；如果a>b，cd，那么a＋c>b＋d.
性质6 如果a>b>0，c>d>0，那么ac>bd.
性质7 如果a>b>0，那么an>bn(n∈N，n≥2).
一.将不等关系表示成不等式(组)
1.读懂题意，找准不等式所联系的量.
2.用适当的不等号连接.
3.多个不等关系用不等式组表示.
二.常见的文字语言与符号语言之间的转换
三．作差法比较两个实数(代数式)大小（“三步一结论”）
1.作差：对要比较大小的两个实数(或式子)作差；
2.变形：对差进行变形
①将差式进行因式分解转化为几个因式相乘.
②将差式通过配方转化为几个非负数之和，然后判断.
3.判断差的符号：结合变形的结果及题设条件判断差的符号；
4.作出结论．
四．利用不等式的性质求取值范围
1.建立待求范围的整体与已知范围的整体的关系，最后利用一次不等式的性质进行运算，求得待求的范围．
2.同向(异向)不等式的两边可以相加(相减)，这种转化不是等价变形，如果在解题过程中多次使用这种转化，就有可能扩大其取值范围．
3.求解这种不等式问题要特别注意不能简单地分别求出单个变量的范围，再去求其他不等式的范围．
考点一 用不等式（组）表示不等关系
【例1】（2023·四川眉山）将一根长为的绳子截成两段，已知其中一段的长度为m，若两段绳子长度之差不小于，则所满足的不等关系为（ ）
A．B．或
C．D．
【答案】D
【解析】由题意,可知另一段绳子的长度为.
因为两段绳子长度之差不小于，所以，化简得：.故选：D
【一隅三反】
1．（2022秋·西藏林芝·高一校考期中）下列说法正确的是（ ）
A．某人月收入x不高于2 000元可表示为“xa”
D．小明的身高x cm，小华的身高y cm，则小明比小华矮表示为“x>y”
【答案】B
【解析】对于A，某人收入x不高于2000元可表示为，A错误；
对于B，变量y不超过a可表示为，B正确；
对于C，变量x至少为a可表示为，C错误；
对于D，小明身高，小华身高，小明比小华矮表示为，D错误.
故选：B.
2．（2023·黑龙江双鸭山）完成一项装修工程，请木工需付工资每人50元，请瓦工需付工资每人40元，现有工人工资预算2000元，设木工人，瓦工人，则请工人满足的关系式是（ ）
A．B．
C．D．
【答案】D
【解析】依题意，请工人满足的关系式是，即.故选：D
3.（2022秋·甘肃庆阳·高一校考阶段练习）在开山工程爆破时，已知导火索燃烧的速度是每秒0.5厘米，人跑开的速度为每秒4米，距离爆破点150米以外（含150米）为安全区．为了使导火索燃尽时人能够跑到安全区，导火索的长度（单位：厘米）应满足的不等式为（ ）
A．B．C．D．
【答案】B
【解析】由题意知导火索的长度（单位：厘米），故导火索燃烧的时间为秒，
人在此时间内跑的路程为米，由题意可得.
故选：B.
4．（2022秋·内蒙古呼和浩特·高一呼市二中校考阶段练习）我国经典数学名著《九章算术》中有这样的一道题：今有出钱五百七十六，买竹七十八，欲其大小率之，向各几何？其意是：今有人出钱576，买竹子78根，拟分大､小两种竹子为单位进行计算，每根大竹子比小竹子贵1钱，问买大､小竹子各多少根？每根竹子单价各是多少钱？则在这个问题中大竹子每根的单价可能为（ ）
A．6钱B．7钱C．8钱D．9钱
【答案】C
【解析】依题意可设买大竹子，每根单价为，
购买小竹子，每根单价为，
所以，
即，即，
因为，
所以，
根据选项，，
所以买大竹子根，每根元.
故选：C
考点二 实数（式）的比较大小
【例2-1】（2023·江苏·高一假期作业）已知，试比较和的大小.
【答案】
【解析】（方法1）因为，所以.
所以.
因为，所以，即；
（方法2）所以，
又，
所以 , 所以.
【一隅三反】
1．（2023·全国·高一假期作业）已知c＞1，且x＝－，y＝－，则x，y之间的大小关系是（ ）
A．x＞yB．x＝y
C．x＜yD．x，y的关系随c而定
【答案】C
【解析】由题设，易知x，y＞0，又，∴x＜y.故选：C.
2．（2023·北京）设， ，则有（ ）
A． B．
C．D．
【答案】A
【解析】，∴.故选：A.
3．（2023·全国·高三对口高考）设实数，，满足①，②，试确定，，的大小关系．
【答案】，当且仅当时．
【解析】因，
所以，当且仅当时，，
，所以，
，所以，综上可知：，当且仅当时．
考点三 利用不等式的性质判断命题的真假
【例3】（2023秋·河南省直辖县级单位）下列命题中正确的是（ ）
A．若，则B．若，，则
C．若，，则D．若，，则
【答案】D
【解析】A选项，当时，，故A错误；
B选项，当，，，时，，，故B错误；
C选项，当，，，时，，故C错误；
D选项，若，，则，即，故D正确．
故选：D.
【一隅三反】
1．（2023春·江苏扬州·高一统考开学考试）对于实数a，b，c，下列命题正确的是（ ）
A．若，则
B．若，则
C．若，则
D．若，则．
【答案】C
【解析】A选项，，故A错误；
B选项，，因不清楚的正负情况，故B错误；
C选项，当时，；
当时，，
当时，，
综上，故C正确；
D选项，，故D错误.故选：C
2．（2023春·上海宝山）下列命题中正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
【答案】B
【解析】取，则，但是，A错误，，但是，C错误，
取，则，但是，D错误，由，可得，所以，
故，B正确，故选：B.
3．（2023·全国·高一假期作业）下列命题为真命题的是（ ）
A．若，则B．若，则
C．若，，则D．若，则
【答案】D
【解析】对于A：当时，，A错误；
对于B：当时，，B错误；
对于C：取满足，，而，此时，C错误；
对于D：当时，则，所以，即，又，所以，D正确.
故选：D.
考点四 利用不等式的性质证明不等式
【例4】（2023·云南）（1）已知，且，证明：．
（2）证明：．
【答案】（1）证明见解析；（2）证明见解析
【解析】证明：（1）由，且，
所以，且
所以，所以，
即；所以，即．
（2）要证，
只需证，
即证；
即证，
即证；即证，显然成立；
所以．
【一隅三反】
1．（2023·内蒙古呼和浩特）证明不等式．
(1)，bd＞0，求证：；
(2)已知a＞b＞c＞0，求证：．
【答案】(1)见详解
(2)见详解
【解析】（1）证明：，
因为，，所以，，又bd＞0，所以，，即.
（2）证明：因为a＞b＞c＞0，所以有，，，，
则，，即有，成立；
因为，，所以，，又，所以，成立.所以，有.
2．（2022·高一课时练习）设，，，，，证明：．
【答案】证明见解析
【解析】证明：因为，所以．
又，所以，
所以．
因为，，，
所以．
考点五 利用不等式的性质求范围
【例5】（2023·海南）已知，求的取值范围__________．
【答案】
【解析】设,则解得
故，
由,故，
由,故，
所以.
故答案为：.
【一隅三反】
1．（2022秋·贵州贵阳·高一校联考期中）已知，，则的取值范围是______.
【答案】
【解析】∵，∴，∵，∴.故答案为：.
2．（2022秋·湖北荆州·高一沙市中学校考阶段练习）已知，，则的取值范围为_________
【答案】
【解析】令，则，
所以，可得，故，
而，故.
故答案为：
3．（2023·福建）若，，，则t的取值范围为______．
【答案】
【解析】设，则，解得．因为，，所以，即．
故答案为：.文字语言
大于，高于，超过
小于，低于，少于
大于等于，至少，不低于
小于等于，至多，不超过
符号语言
>