上海市位育中学2024-2025学年高二上学期10月期中数学试卷(无答案)

这是一份上海市位育中学2024-2025学年高二上学期10月期中数学试卷(无答案)，共8页。试卷主要包含了填空题，选择题，解答题等内容，欢迎下载使用。
1．直线l和平面α相交于点A，用集合符号表示为________．
2．已知空间两个角和，若，则________．
3．一个水平放置的边长为2的正三角形的直观图面积为________．
4．将长为3，宽为2的矩形绕着较长边所在的直线旋转一周，所形成的几何体的体积为________．
5．已知球的表面积为36π，则该球的体积为________．
6．已知圆锥的底面半径是1，它的侧面展开图是一个半圆，则这个圆锥的侧面积为________．
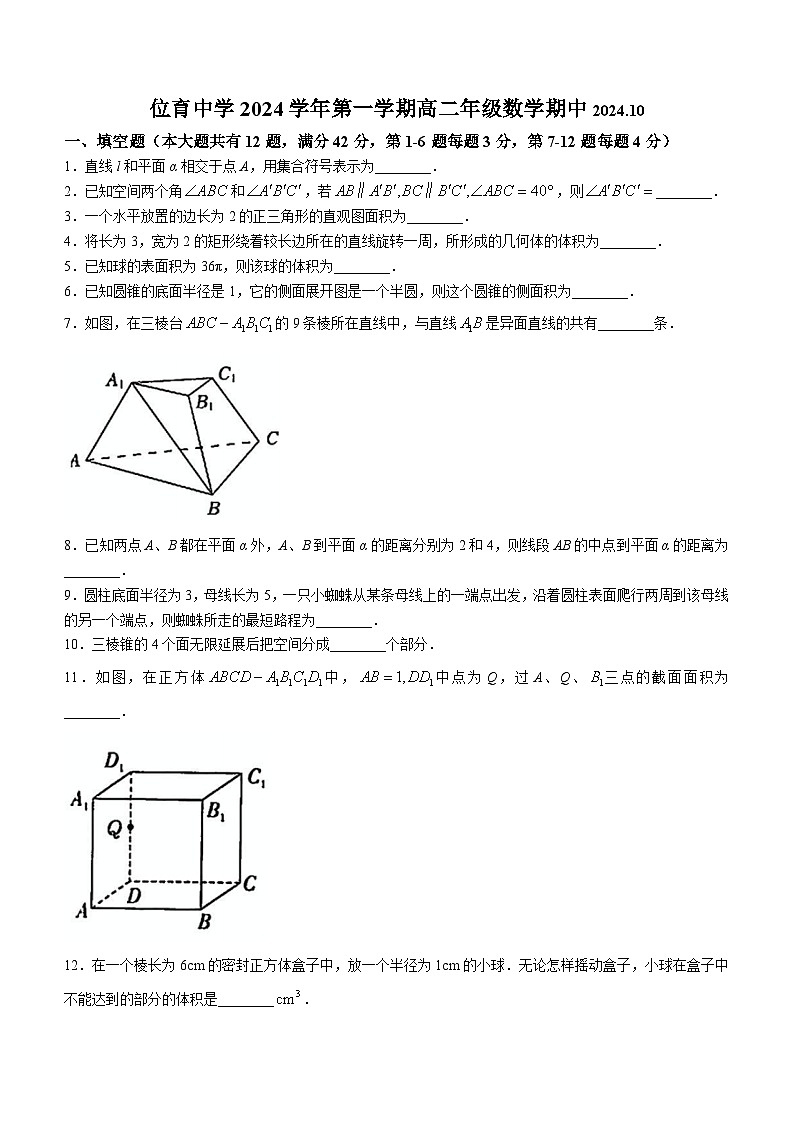
7．如图，在三棱台的9条棱所在直线中，与直线是异面直线的共有________条．
8．已知两点A、B都在平面α外，A、B到平面α的距离分别为2和4，则线段AB的中点到平面α的距离为________．
9．圆柱底面半径为3，母线长为5，一只小蜘蛛从某条母线上的一端点出发，沿着圆柱表面爬行两周到该母线的另一个端点，则蜘蛛所走的最短路程为________．
10．三棱锥的4个面无限延展后把空间分成________个部分．
11．如图，在正方体中，中点为Q，过A、Q、三点的截面面积为________．
12．在一个棱长为6cm的密封正方体盒子中，放一个半径为1cm的小球．无论怎样摇动盒子，小球在盒子中不能达到的部分的体积是________．
二、选择题（本大题共有4题，每题4分，满分16分）
13．设a、b为平面M外的两条直线，且，那么是的（ ）条件
A．充分非必要B．必要非充分C．充要D．非充分非必要
14．已知a，b表示两条不同的直线，α，β表示两个不同的平面，下列说法错误的是（ ）
A．若，则B．若，则
C．若，则D．若，则或
15．如图所示，一个灯笼由一根提竿PQ和一个圆柱组成，提竿平行于圆柱的底面，在圆柱上下底面圆周上分别有两点A、B，AB与圆柱的底面不垂直，则在圆柱绕着其旋转轴旋转一周的过程中，直线PQ与直线AB垂直的次数为（ ）
A．2B．4C．6D．8
16．如图所示，正三棱柱的所有棱长为1，点P、M、N分别为棱的中点，点Q为线段MN上的动点（含端点）．当点Q由点N出发向点M运动的过程中，以下结论中正确的是（ ）
A．直线与直线CP可能相交B．直线与直线CP始终异面
C．直线与直线CP可能垂直D．直线与直线BP不可能垂直
三、解答题（本大题共有5题，满分42分）
17．（本题满分8分）用文字语言表述“线面平行的判定定理”，写出已知、求证并证明．
18．（本题满分8分，第1小题满分4分，第2小题满分4分）
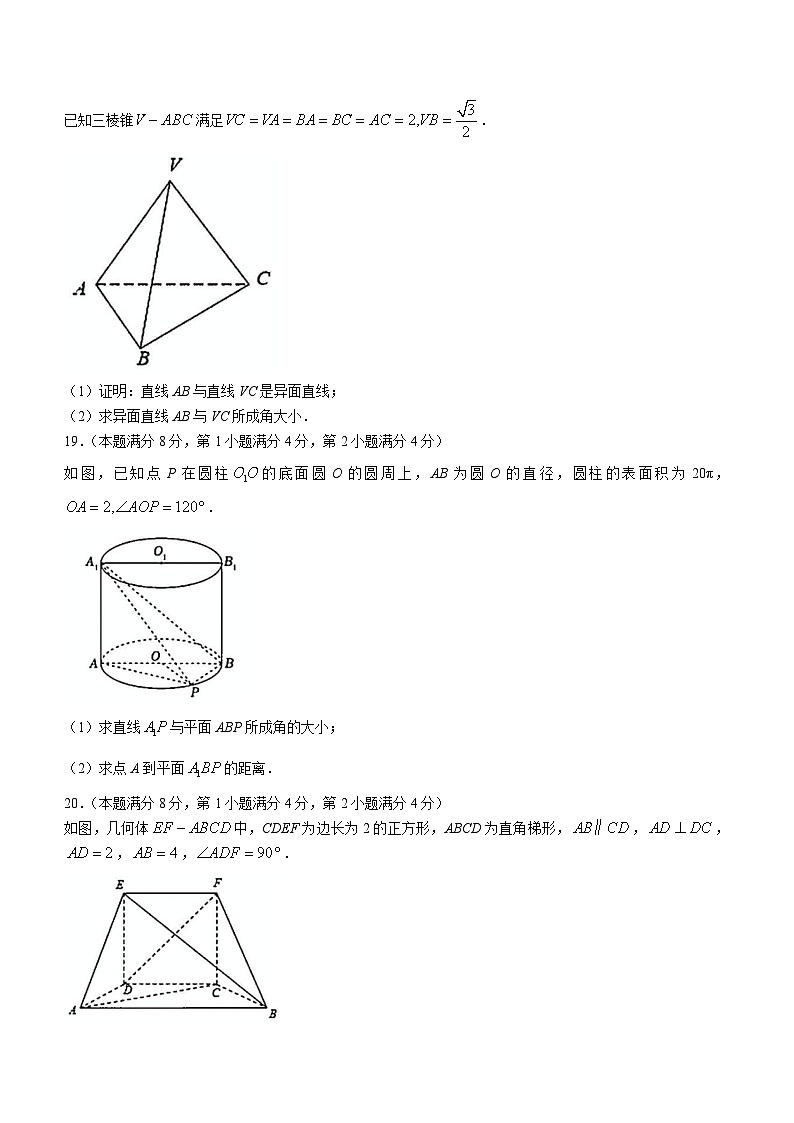
已知三棱锥满足．
（1）证明：直线AB与直线VC是异面直线；
（2）求异面直线AB与VC所成角大小．
19．（本题满分8分，第1小题满分4分，第2小题满分4分）
如图，已知点P在圆柱的底面圆O的圆周上，AB为圆O的直径，圆柱的表面积为20π，．
（1）求直线与平面ABP所成角的大小；
（2）求点A到平面的距离．
20．（本题满分8分，第1小题满分4分，第2小题满分4分）
如图，几何体中，CDEF为边长为2的正方形，ABCD为直角梯形，，，，，．
（1）求证：平面；
（2）求几何体的体积．
21．（本题满分10分，第1小题满分4分，第2小题满分6分）
如图，在四面体ABCD中，平面，点M为AD上一点，且，连接BM，CM．
（1）；
（2）求二面角．的大小．
参考答案
一、填空题
1． 2．40°或140° 3．； 4． 5． 6．
7．3 8．3或1 9． 10．15 11． 12．
11．【答案】
【解析】截面是如图所示的等腰梯形，其中为的中点．
因为，所以该梯形的高为，
所以截面面积．
答案：
12．【答案】
【解析】在正方体的8个顶点处的单位立方体空间内，
小球不能到达的空间为：
除此之外，在以正方体的棱为一条棱的12个的正四棱柱空间内，
小球不能到达的空间共为其他空间小球均能到达．
故小球不能到达的空间体积为：．
故答案为：
二、选择题
13．A 14．C 15．A 16．B
15．【答案】A
【解析】作出平面，使得平面，当时，平面或平面，结合旋转分析可知有两次使得．故选：A．
16．【答案】B
【解析】在正三棱柱中，点分别为棱的中点，
平面平面平面，
四点不共面，直线与始终异面，故A错误，B正确；
对于C，设，
则，
若直线与直线垂直，则
，解得，
不存在点使得直线与直线垂直，故C错误；
对于D，连接，如图，为的中点，，
平面平面，
平面，又平面，
当点在的位置时，直线与直线垂直，故错误．故选：B．
三．解答题
17．平面外一条直线与此平面内一条直线平行，则该直线与此平面平行；
已知，求证；证明略
18．（1）证明略 （2）
19．（1） （2）
20．【答案】（1）见解析 （2）
【解析】（1）由题意得，，且，
平面四边形CDEF为正方形，，
由平面，
又四边形为直角形，，
，则有，
由平面，
（2）连结，过作的垂线，垂足为，易见平面，且，
，
几何体的体积为．
21．【答案】（1）见解析 （2）
【解析】（1）证明：因为平面平面，所以，
因为平面，所以平面，
因为平面，所以；
（2）取的中点，连接，过作于，过作于，
连接，因为在平面中，，所以，
由（1）知，所以因为平面，
所以平面，因为平面，所以
因为平面MEH，所以平面，
因为平面，所以，所以为二面角的平面角，
因为，所以，
在中，，所以，
所以，所以二面角的大小为．