广东省东莞市东莞外国语学校2024-2025学年高三上学期第2次月考（10月）数学试题（原卷及解析版）

这是一份广东省东莞市东莞外国语学校2024-2025学年高三上学期第2次月考（10月）数学试题（原卷及解析版），文件包含广东省东莞市东莞外国语学校2024-2025学年高三上学期第2次月考10月数学试题原卷版docx、广东省东莞市东莞外国语学校2024-2025学年高三上学期第2次月考10月数学试题解析版docx等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。
命题人：桂林峰 审题人：张立东
说明：本试卷共4页，19小题，满分150分，考试用时120分钟.
注意事项：1．答卷前，考生请用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B铅笔将试卷类型（A）填涂在答题卡相应位置上.
2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑.如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上.
一、选择题：本大题共8小题，每小题5分，满分40分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 设，，则（ ）
A. B. C. D.
【答案】A
【解析】
【分析】联立集合A与集合B方程组，解出来的解组就是.
【详解】根据题意知联立集合A与集合B方程组得，
解之可得或，所以.
故选：A
2. “”是“”的（ ）
A. 必要而不充分条件B. 充分而不必要条件
C. 充要条件D. 既不充分也不必要条件
【答案】B
【解析】
【分析】分析两个集合和的关系，从而推出命题之间的关系
【详解】解不等式，得
而集合是集合的真子集，所以“”是“”的充分而不必要条件
故选：B
3. 函数的最小值为（ ）
A. 8B. 6C. 4D. 10
【答案】D
【解析】
【分析】
由然后利用基本不等式可求得答案.
【详解】因为，所以，
当且仅当即等号成立，
所以函数的最小值为10，
故选：D.
【点睛】本题考查了利用基本不等式求最值，注意等号成立的条件，属于基础题.
4. 学校组织同学参加社会调查，某小组共有5名男同学，4名女同学．现从该小组中选出3位同学分别到，，三地进行社会调查，若选出的同学中男女均有，则不同安排方法有（ ）
A. 70种B. 140种C. 420种D. 840种
【答案】C
【解析】
【分析】将情况分为2男1女和2女1男两种情况，相加得到答案.
【详解】2男1女时：
2女1男时：
共有420种不同的安排方法
故答案选C
【点睛】本题考查了排列组合的应用，将情况分为2男1女和2女1男两种情况是解题的关键.
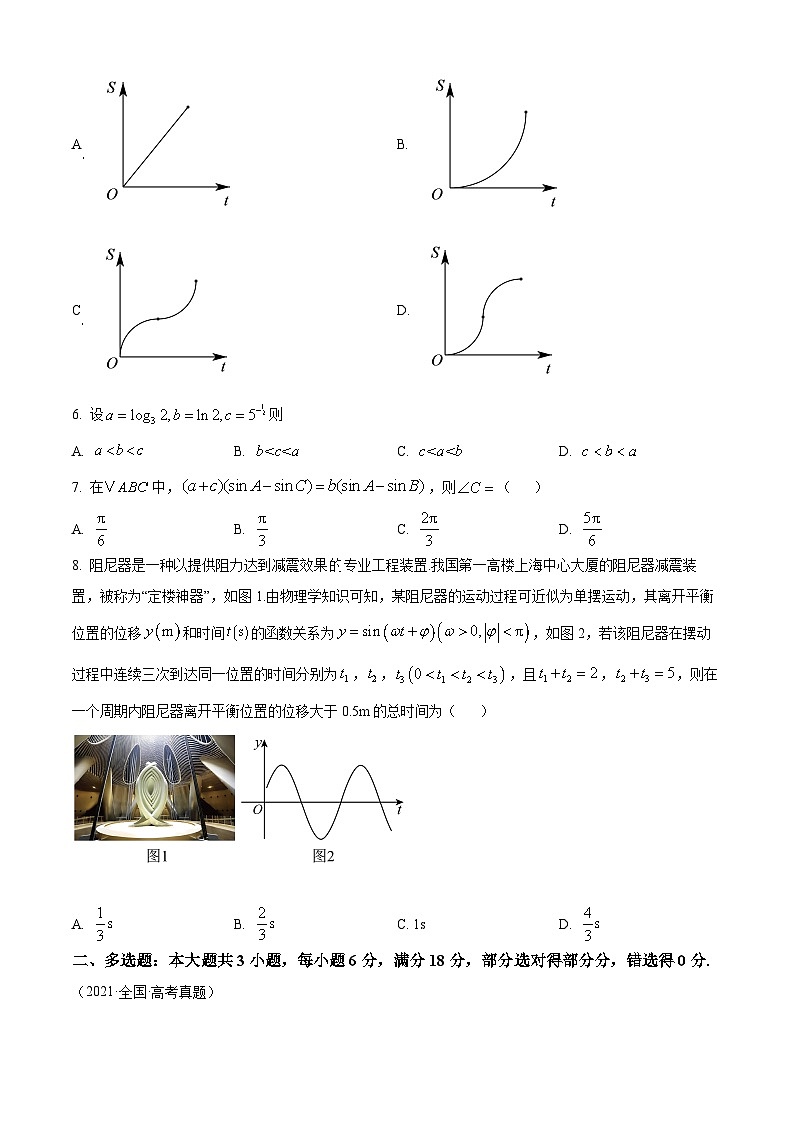
5. 如图，直线l和圆C，当l从l0开始在平面上绕点O按逆时针方向匀速转到（转到角不超过90°）时，它扫过的圆内阴影部分的面积S是时间t的函数，这个函数的图像大致是
A. B.
C. D.
【答案】D
【解析】
【分析】由题意可知：S变化情况为“一直增加，先慢后快，过圆心后又变慢”，据此确定函数的大致图像即可.
【详解】观察可知面积S变化情况为“一直增加，先慢后快，过圆心后又变慢”，
对应的函数的图象是变化率先变大再变小，由此知D符合要求.
故选D.
【点睛】本题主要考查实际问题中的函数图像，函数图像的变化趋势等知识，意在考查学生的转化能力和计算求解能力.
6. 设则
A. B. C. D.
【答案】C
【解析】
【分析】由及可比较大小.
【详解】∵，∴，即．
又．∴．综上可知：
故选C.
【点睛】本题主要考查了指数与对数的运算性质及对数函数的单调性比较大小，属于中档题.
7. 在中，，则（ ）
A. B. C. D.
【答案】B
【解析】
【分析】利用正弦定理的边角变换与余弦定理即可得解.
【详解】因为，
所以由正弦定理得，即，
则，故，
又，所以.
故选：B.
8. 阻尼器是一种以提供阻力达到减震效果的专业工程装置.我国第一高楼上海中心大厦的阻尼器减震装置，被称为“定楼神器”，如图1.由物理学知识可知，某阻尼器的运动过程可近似为单摆运动，其离开平衡位置的位移和时间的函数关系为，如图2，若该阻尼器在摆动过程中连续三次到达同一位置的时间分别为，，，且，，则在一个周期内阻尼器离开平衡位置的位移大于0.5m的总时间为（ ）

A. B. C. 1sD.
【答案】C
【解析】
【分析】先根据周期求出，再解不等式，得到的范围即得解.
【详解】因为，，，所以，又，所以，
则，由可得，
所以，，
所以，，故，
所以在一个周期内阻尼器离开平衡位置位移大于0.5m的总时间为1s.
故选：C.
二、多选题：本大题共3小题，每小题6分，满分18分，部分选对得部分分，错选得0分.
（2021·全国·高考真题）
9. 有一组样本数据，，…，，由这组数据得到新样本数据，，…，，其中(为非零常数，则（ ）
A. 两组样本数据的样本平均数相同
B. 两组样本数据的样本中位数相同
C. 两组样本数据的样本标准差相同
D. 两组样本数据的样本极差相同
【答案】CD
【解析】
【分析】A、C利用两组数据的线性关系有、，即可判断正误；根据中位数、极差的定义，结合已知线性关系可判断B、D的正误.
【详解】A：且，故平均数不相同，错误；
B：若第一组中位数为，则第二组的中位数为，显然不相同，错误；
C：，故方差相同，正确；
D：由极差的定义知：若第一组的极差为，则第二组的极差为，故极差相同，正确；
故选：CD
(2021高考北京改编·)
10. 若点关于轴对称点为，则的取值可以为（ ）
A. B. C. D.
【答案】AC
【解析】
【分析】根据对称性得到，，化简后得到，对四个选项一一计算，得到答案.
【详解】由题意得，，
，故，
，故，
A选项，，A正确；
B选项，，B错误；
C选项，，C正确；
D选项，由B选项知，，D错误.
故选：AC
11. 已知函数在处取得极值，则（ ）
A. B. C. D.
【答案】ABC
【解析】
【分析】求导得到导函数，再次求导证明单调递增，根据零点存在定理得到，AB正确，代换得到，C正确，若D成立得到，矛盾，得到答案.
【详解】，则，恒成立，
故单调递增， ，，
故存在，函数在上单调递减，在上单调递增，AB正确；
，，
，故C正确；
若，，则，，
，则，这与矛盾，故D错误.
故选：ABC.
三、填空题：本大题共3小题，每小题5分，满分15分
（必修一P219例4（3）改编）
12. 求值：__________．
【答案】
【解析】
【分析】直接利用两角和的正切公式计算可得；
【详解】解：
故答案为：
（选择性必修三P 改编）
13. 甲和乙两个箱子中各装有个球，其中甲箱中有个白球､个红球，乙箱中有个红球､个白球.掷一枚质地均匀的骰子，如果点数为或，从甲箱子随机摸出个球；如果点数为，从乙箱子中随机摸出个球.则摸到红球的概率为___________.
【答案】##0.7
【解析】
【分析】分别计算出从甲箱中摸到红球的概率和从乙箱中摸到红球的概率，然后利用概率的加法公式即可.
【详解】从甲箱中摸红球：掷到点数为5或6的概率为，再从甲箱中摸到红球的概率为，
故从甲箱中摸到红球概率为；
从乙箱中摸红球：掷到点数为1，2，3，4的概率为，再从乙箱中摸到红球的概率为，
故从乙箱中摸到红球的概率为；
综上所述：摸到红球的概率为.
故答案为：
14. 定义在上的函数满足：①当时，②.若函数的零点从小到大依次记为，则当时，_______.
【答案】
【解析】
【分析】在同一坐标系内做出和的图象，根据图象得到，的对称关系，把转化为等比数列前项和即可求解.
【详解】在同一坐标系内做出和的图象如图所示：
当时，利用对称性，依次有：，
，
，
，
所以.
故答案为：.
【点睛】方法点睛：已知函数有零点，求零点和（积）的常用方法：
（1）直接法：直接求解方程得到方程的根，再直接求和（积）；
（2）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解.
四、解答题：本大题共5小题，满分77分．解答须写出文字说明、证明过程和演算步骤．
（2014·福建·高考真题）
15. 函数．
（1）求的值；
（2）求函数的最小正周期及单调递增区间．
【答案】（1）；（2），的单调递增区间为.
【解析】
【详解】试题分析：（1）借助题设直接运用诱导公式化简求解；（2）借助题设条件和二倍角公式求解．
试题解析:
（1），
（2）因为．
所以， 由，
得，所以的单调递增区间为．
考点：三角函数的图象及诱导公式二倍角公式的运用．
（2007年海南卷）
16. 设函数
（1）讨论的单调性；
（2）求在区间的最大值和最小值．
【答案】（1）函数在上单调递增；在上单调递减；
（2）在区间上的最大值为，最小值为.
【解析】
【分析】（1）先求函数的定义域，解不等式求出函数的单调递增区间，解不等式求出函数的单调递减区间；（2）根据函数的单调性求出函数的最值.
【小问1详解】
函数的定义域为，
又.
令，解得或；令，解得.
所以函数在上单调递增；在上单调递减；
【小问2详解】
由（1）可得：函数在区间内单调递减，在内单调递增.
所以当时，函数取得最小值，
又，，
而，
所以当时，函数取得最大值：.
即在区间上的最大值为，最小值为.
17. 长跑可提高呼吸系统和心血管系统机能，较长时间有节奏的深长呼吸，能使人体呼吸大量的氧气，吸收氧气量若超过平时的倍，就可以抑制人体癌细胞的生长和繁殖.其次长跑锻炼还改善了心肌供氧状态，加快了心肌代谢，同时还使心肌纤维变粗，心收缩力增强，从而提高了心脏工作能力.为了调查学生喜欢跑步是否与性别有关，高三年级特选取了200名学生进行了问卷调查，得到如下的列联表：已知在这200名学生中随机抽取1人抽到喜欢跑步的概率为0.6．
（1）判断：是否有90%的把握认为喜欢跑步与性别有关？
（2）从上述不喜欢跑步的学生中用分层抽样的方法抽取8名学生，再在这8人中抽取3人调查其喜欢的运动，用X表示3人中女生的人数，求X的分布及数学期望．
附：，其中．
【答案】（1）无90%把握认为喜欢跑步与性别有关，理由见解析
（2）分布列见解析，
【解析】
【分析】（1）计算出喜欢跑步和不喜欢跑步的人数，完善列联表，作出零假设，计算出卡方，与2.706比较后得到结论；
（2）由分层抽样得到抽取女生2名，男生6名，得到的分布列，计算出期望值.
小问1详解】
由题可知，从200名学生中随机抽取1人抽到喜欢跑步的概率为0.6，
故喜欢跑步的人有（人），不喜欢跑步的人有（人）．
∴，，，，
零假设学生对长跑的喜欢情况与性别无关联，
根据题意，由列联表中的数据，
可得，
所以在的独立性检验中，不能推翻，故无90%把握认为喜欢跑步与性别有关．
【小问2详解】
按分层抽样，设女生名，男生名，，解得，，
∴从不喜欢跑步的学生中抽取女生2名，男生6名，
故的可能取值为0，1，2．
，，，
故X的分布为：
∴．
18. 设函数，，．
（1）时，求在处切线方程；
（2）若在y轴右侧，函数图象恒不在函数的图象下方，求实数a的取值范围；
（3）证明：当时，．
【答案】（1）
（2）
（3）证明见解析
【解析】
【分析】（1）利用导数的几何意义求解即可；
（2）设函数，求得，令，求得，分和，两种情况讨论，求解函数的单调，进而求得的取值范围.
（3）取，由（2）知，令，，令，化简得到，进而证得结论.
【小问1详解】
时，，
∵，∴，
∵，则切线方程为，即.
【小问2详解】
设函数，则，
令，则，
当，即时，，即，
即，
所以成立，此时符合题意；
当，即时，令，解得，
所以在区间上单调递减，
又由，此时在上单调递减，
所以，显然不满足题意，
综上可得，实数a的取值范围为.
【小问3详解】
取，由（2）知在上恒成立，当且仅当时，等号成立，
因为，令，代入得到，
即，且，
令，，即，
代入化简得到，
所以成立．
【点睛】方法点睛：利用导数证明或判定不等式问题：
1．通常要构造新函数，利用导数研究函数的单调性与极值（最值），从而得出不等关系；
2．利用可分离变量，构造新函数，直接把问题转化为函数的最值问题，从而判定不等关系；
3．适当放缩构造法：根据已知条件适当放缩或利用常见放缩结论，从而判定不等关系；
4．构造“形似”函数，变形再构造，对原不等式同解变形，根据相似结构构造辅助函数.
19. 已知，集合其中.
（1）求中最小的元素；
（2）设，，且，求的值；
（3）记，，若集合中的元素个数为，求.
【答案】（1）7 （2）或10
（3）
【解析】
【分析】（1）根据集合新定义，确定中最小的元素即可；
（2）根据集合中的元素可得，设，，分别讨论当时，当时，当时，的取值情况，即可得结论；
（3）设，则，其中，，所以，根据组合数的运算性质确定与的关系，即可求得的值.
【小问1详解】
中的最小元素为.
【小问2详解】
由题得，设，.
①当时，或或或或或.
经检验，当时，，符合题意，
所以.
②当时，或或或.
经检验，当时，，符合题意，
所以.
③当时，不符合题意.
因此，或10.
【小问3详解】
设，则，其中，
，所以，
设，则.
因为，
所以
.
因为，
所以，所以，
又因为，所以.
【点睛】方法点睛：解决以集合为背景的新定义问题，注意两点：
（1）根据集合定义式，确定集合中元素的特点，结合指数运算确定指数的取值情况从而得集合中的元素性质；
（2）确定集合中的元素个数为时，结合组合数的运算性质确定与的关系.
喜欢跑步
不喜欢跑步
合计
男生
80
女生
20
合计
喜欢跑步
不喜欢跑步
合计
男生
80
60
140
女生
40
20
60
合计
120
80
200
0
1
2