高中数学人教B版 (2019)选择性必修 第一册2.3.3 直线与圆的位置关系随堂练习题

这是一份高中数学人教B版 (2019)选择性必修 第一册2.3.3 直线与圆的位置关系随堂练习题，共52页。

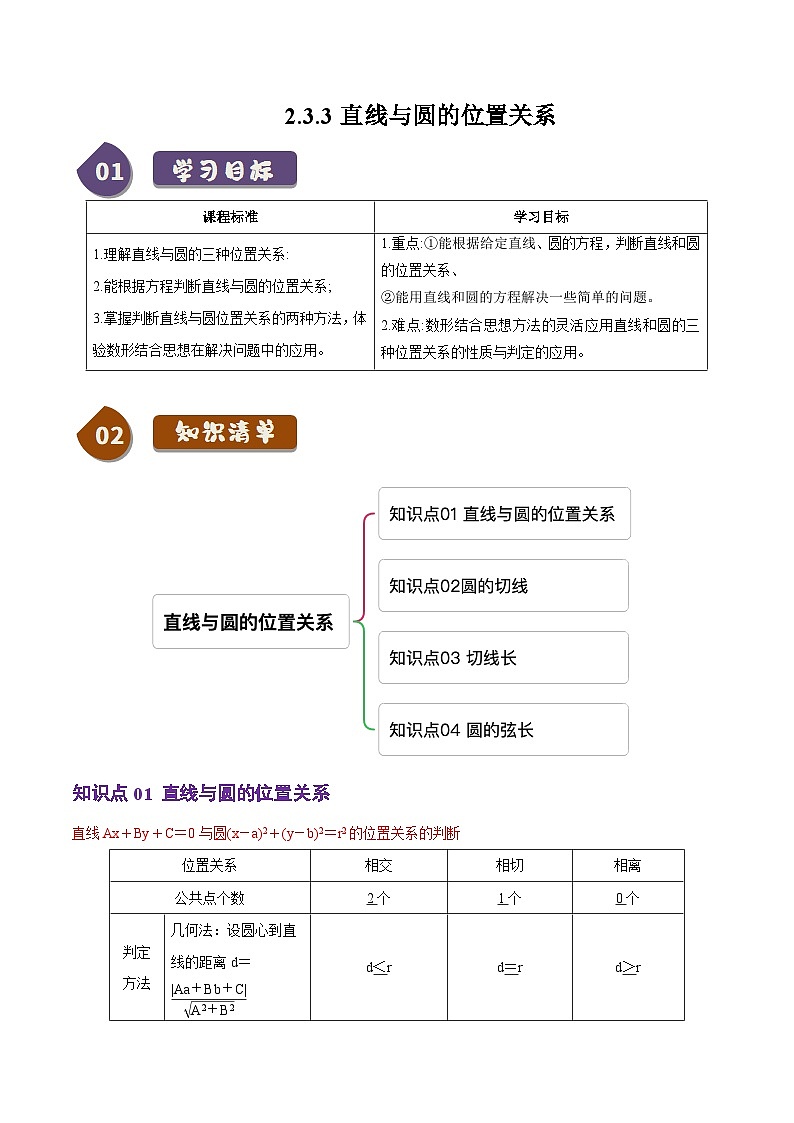
知识点01 直线与圆的位置关系
直线Ax＋By＋C＝0与圆(x－a)2＋(y－b)2＝r2的位置关系的判断
【即学即练1】（22-23高二上·新疆喀什·期末）直线y=x+1与圆x2+y2=1的位置关系为（ ）
A．相切B．相交但直线过圆心
C．相交但直线不过圆心D．相离
【答案】C
【分析】利用圆心到直线的距离和半径的大小关系即可判断直线与圆的位置关系.
【详解】圆x2+y2=1的圆心为0,0，半径为1，
故圆心到直线y=x+1的距离为11+1=120上，则过A的圆的切线方程为 .
【答案】y=x+1
【分析】利用垂直直线的斜率关系和直线方程相关概念直接求解.
【详解】因为点A0,1在圆C:x-12+y2=r2r>0上，
所以过A的圆的切线方程和AC垂直，
因为A0,1，C1,0，所以kAC=1-00-1=-1，所以切线方程斜率为-1-1=1，
所以切线方程为y=1×x-0+1，即y=x+1.
故答案为：y=x+1
【即学即练4】（23-24高三上·浙江·阶段练习）过圆x2+y2=1上点P-22,22的切线方程为 ．
【答案】y=x+2
【分析】由圆的切线性质求出切线斜率，利用点斜式方程即可得.
【详解】由题知，kOP=-1，则切线斜率k=1，
所以切线方程为y-22=x--22，整理为y=x+2．
故答案为：y=x+2
知识点03 切线长
1.从圆x2＋y2＋Dx＋Ey＋F＝0(D2＋E2－4F>0)外一点M(x0，y0)引圆的两条切线，切线长为 eq \r(x\\al(2,0)＋y\\al(2,0)＋Dx0＋Ey0＋F).
2.两切点弦长：利用等面积法，切线长a与半径r的积的2倍等于点M与圆心的距离d与两切点弦长b的积，即b＝eq \f(2ar,d).
【即学即练5】（22-23高二上·重庆北碚·阶段练习）过点A2,3作圆M:x2+y2=1的一条切线，切点为B，则AB=（ ）
A．3B．23C．7D．10
【答案】B
【分析】先求得圆M的圆心坐标和半径，再利用切线长定理即可求得AB的值.
【详解】因为圆M:x2+y2=1，
所以圆M的圆心为M(0,0)，半径为r=1，
因为AB与圆M相切，切点为B，
所以AB⊥BM，则AB2+r2=AM2，
因为AM=22+32=13，
所以AB=AM2-r2=13-1=23.
故选：B.
【即学即练6】（24-25高二上·全国·课前预习）如图，直线与圆相离，过直线上一点作圆的切线，切线长的最小值= ．
【答案】d2-r2
知识点04 圆的弦长
直线和圆相交，求被圆截得的弦长通常有两种方法：
(1)几何法：因为半弦长eq \f(L,2)、弦心距d、半径r构成直角三角形，所以由勾股定理得L ＝2eq \r(r2－d2).
(2)代数法：若直线y＝kx＋b与圆有两交点A(x1，y1)，B(x2，y2)，则有：|AB|＝eq \r(1＋k2)|x1－x2|＝eq \r(1＋\f(1,k2))|y1－y2|.
【即学即练7】（2024·内蒙古赤峰·一模）已知圆C:x-22+y2=4，直线l:y=-x+1被圆C截得的弦长为 .
【答案】14
【分析】根据直线和圆的位置关系，利用点到直线的距离公式和弦长公式求解.
【详解】解：由题意可得，圆心为2,0，半径r=2，
弦心距d=2+0-12=22，
故直线l被C截得的弦长为2r2-d2=14，
故答案为：14
【即学即练8】（22-23高二上·河北保定·期末）直线l:x-y+1=0与圆C:x2+y2-2x-3=0交于A,B两点，则△AOB的面积为（ ）
A．3B．2C．22D．32
【答案】B
【分析】依题意，作出图形，求出圆心坐标和半径，过圆心C(1,0)作CD⊥AB于D，分别计算|CD|和|AB|，即可求得△AOB的面积.
【详解】
如图，由圆C:x2+y2-2x-3=0配方得，(x-1)2+y2=4，知圆心为C(1,0),半径为2，
过点C(1,0)作CD⊥AB于D，由C(1,0)到直线l:x-y+1=0的距离为|CD|=22=2,
则|AB|=2|AD|=222-(2)2=22,
故△AOB的面积为12|AB|⋅|CD|=12×22×2=2.
故选：B.
难点：最值问题
示例1：（24-25高二上·江苏徐州·阶段练习）已知曲线1-x=4-y2，则x2+y-42的最大值，最小值分别为（ ）
A．17＋2，17－2B．17＋2，5
C．37，17－2D．37，5
【答案】C
【分析】由题意可得曲线1-x=4-y2表示的图形为以A(1,0)为圆心，2为半径的半圆，x2+(y-4)2表示半圆上的动点与点P(0,4)的距离，作出图象，结合图象求解即可．
【详解】由1-x=4-y2，可知x≤1，-2≤y≤2，
且有(x-1)2+y2=4，表示的图形为以A(1,0)为圆心，2为半径的半圆，如图所示：
B1,2,C1,-2

又因为x2+(y-4)2表示半圆上的动点与点P(0,4)的距离，
又因为|PA|=12+42=17，
所以x2+(y-4)2的最小值为|PA|-2=17-2，
当动点与图中C(1,-2)点重合时，x2+(y-4)2取最大值|PC|=(1-0)2+(4+2)2=37，
故选：C．
【题型1：直线与圆有关的位置关系】
例1．（24-25高三上·四川成都·开学考试）在同一平面直角坐标系中，直线mx-y+1=0m∈R与圆x2+y2=2的位置不可能为（ ）
A．B．
C．D．
【答案】C
【分析】由圆的位置和直线所过定点，判断直线与圆的位置关系.
【详解】圆x2+y2=2的圆心坐标为0,0，半径为2，
直线mx-y+1=0m∈R过圆内定点0,1，斜率可正可负可为0，
ABD选项都有可能，C选项不可能.
故选：C.
变式1．（23-24高二下·云南曲靖·期末）已知圆C:(x-2)2+y2=16，直线l:mx+y-3m-1=0，则下列结论中正确的是（ ）
A．直线l恒过定点2,1B．直线l与圆C相切
C．直线l与圆C相交D．直线l与圆C相离
【答案】C
【分析】求出圆C的圆心和半径，直线l所过的定点，再由该定点与圆的位置关系判断直线与圆的位置即可.
【详解】圆C:(x-2)2+y2=16的圆心C(2,0)，半径r=4，
直线l:m(x-3)+y-1=0恒过定点(3,1)， 显然(3-2)2+12=21=r，
故直线l与圆C相离．
故选：C．
变式4．（2007高二·全国·竞赛）直线y=33x绕原点逆时针方向旋转30°后，所得直线与圆x-22+y2=3的位置关系为（ ）
A．直线过圆心B．直线与圆相交，但不过圆心
C．直线与圆相切D．直线与圆没有公共点
【答案】C
【分析】先求出直线y=33x绕原点逆时针方向旋转30°后的直线方程，再由点到直线的距离公式求出则圆心2,0到直线的距离，与半径比较，即可得出答案.
【详解】直线y=33x的倾斜角为30°，
直线y=33x绕原点逆时针方向旋转30°后直线的倾斜角为60°，
旋转后的直线方程为y=3x，
则圆心2,0到直线的距离d=233+1 =3=r，
∴直线与圆相切.
故选：C.
变式5.（10-11高二上·湖南益阳·阶段练习）如果直线ax+by-1=0与圆x2+y2=1有两个不同的交点，则点Pa,b与圆的位置关系为（ ）
A．P在圆外B．P在圆上
C．P在圆内D．P与圆的位置不确定
【答案】A
【分析】根据直线ax+by-1=0与圆x2+y2=1有两个不同的交点，知道它们相交.借助d1,进而得到点Pa,b与圆的位置关系.
【详解】直线ax+by-1=0与圆x2+y2=1有两个不同的交点，则它们相交.
根据d=1a2+b21，即a2+b2>1.则点Pa,b与圆的位置关系为P在圆外.
故选：A.
变式6.(多选)（2024·全国·模拟预测）已知直线l:mx+ny-r2=0与圆C:x2+y2=r2，点Pm,n，则下列命题中是假命题的是（ ）.
A．若点P在圆C外，则直线l与圆C相离B．若点P在圆C内，则直线l与圆C相交
C．若点P在圆C上，则直线l与圆C相切D．若点P在直线l上，则直线l与圆C相切
【答案】AB
【分析】根据直线和圆相切、相交、相离的等价条件进行求解即可.
【详解】对于A，因为点Pm,n在圆C外，所以m2+n2>r2，
则圆心C0,0到直线l的距离为d=0×m+0×n-r2m2+n2=r2m2+n2