

辽宁省沈阳市2023_2024学年高二数学上学期10月月考试题
展开这是一份辽宁省沈阳市2023_2024学年高二数学上学期10月月考试题,共8页。试卷主要包含了 直线, 已知直线, 表示的曲线为, 若点在圆上,则的取值范围为, 在下列四个命题中,正确的是等内容,欢迎下载使用。
1. 直线:的一个方向向量可以是()
A. B. C. D.
2. 已知直线:,:,则“”是“”的()
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
3. 向量,,在直线l方向向量上的投影向量相等,则直线l的斜率为()
A. 1B. -1C. 2D. -2
4. 已知圆,则当圆的面积最小时,圆上的点到坐标原点的距离的最大值为()
A. B. C. D.
5. 表示的曲线为( )
A. 两个半圆B. 一个圆
C. 半个圆D. 两个圆
6. 如图,已知正方形的边长为2,,分别是,的中点,平面,且,则与平面所成角的正弦值为()
A. B. C. D.
7. 若点在圆上,则的取值范围为()
A. B. C. D.
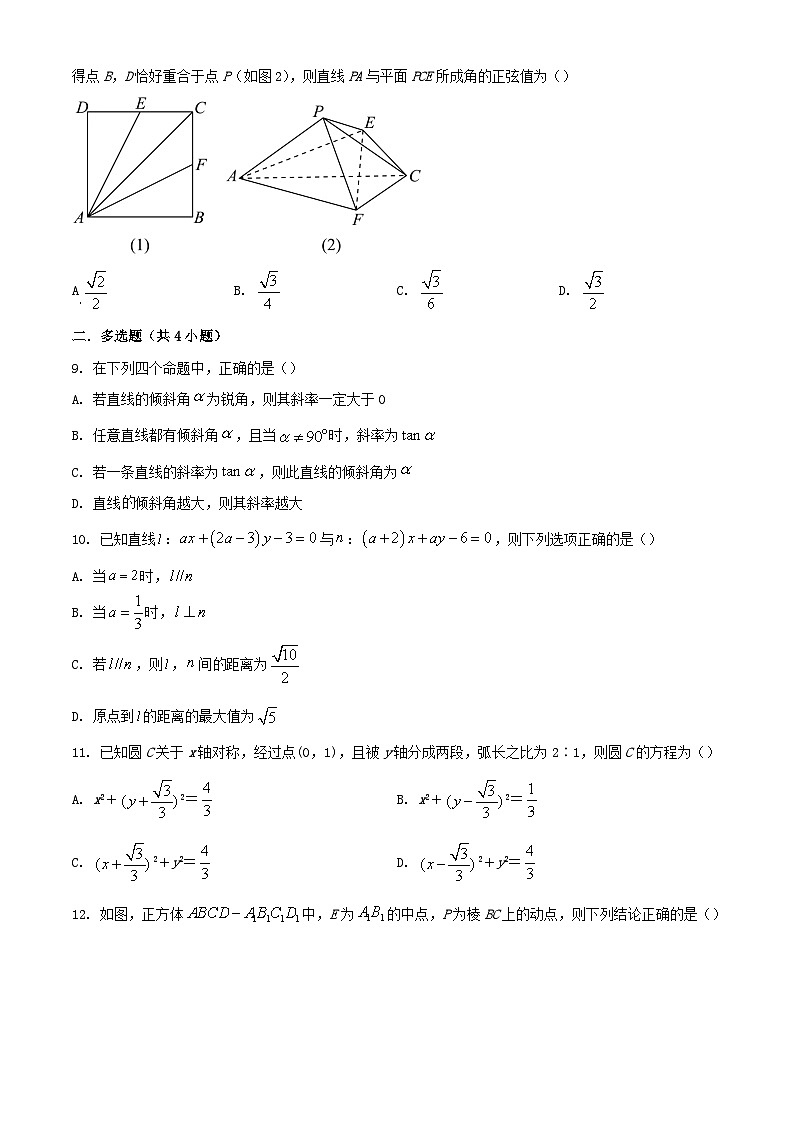
8. 若正方形ABCD的边长为a,E,F分别为CD,CB的中点(如图1),沿AE,AF将△ADE,△ABF折起,使得点B,D恰好重合于点P(如图2),则直线PA与平面PCE所成角的正弦值为()
AB. C. D.
二.多选题(共4小题)
9. 在下列四个命题中,正确的是()
A. 若直线的倾斜角为锐角,则其斜率一定大于0
B. 任意直线都有倾斜角,且当时,斜率为
C. 若一条直线的斜率为,则此直线的倾斜角为
D. 直线倾斜角越大,则其斜率越大
10. 已知直线:与:,则下列选项正确的是()
A. 当时,
B. 当时,
C. 若,则,间距离为
D. 原点到的距离的最大值为
11. 已知圆C关于x轴对称,经过点(0,1),且被y轴分成两段,弧长之比为2∶1,则圆C的方程为()
A. x2+2=B. x2+2=
C. 2+y2=D. 2+y2=
12. 如图,正方体中,E为的中点,P为棱BC上的动点,则下列结论正确的是()
A. 存在点P,使平面
B. 存在点P,使
C. 四面体的体积为定值
D. 二面角的余弦值取值范围是
三.填空题(共4小题)
13. 过点引一直线,使点和到的距离相等,则直线的方程是:____________
14. 点在圆外,则a的取值范围为______.
15. 已知直线,直线,其中,若直线,与两坐标轴围成一个凸四边形,则此四边形面积的取值范围是_______.
16. 如图,已知ABCD和CDEF都是直角梯形,,,,二面角的平面角为.设M,N分别为AE,BC的中点,直线BM与平面ADE所成角的正弦值为_________.
四.解答题(共6小题)
17. 已知直线与直线.
(1)若,求m的值,并求出两平行线间的距离;
(2)若点在直线上,直线l过点P,且在两坐标轴上的截距互为相反数,求直线l的方程.
18. 已知中,,角A的平分线在轴上.
(1)求点关于轴的对称点的坐标及边,边所在直线的方程;
(2)求的外接圆的方程.
19. 求满足下列条件的圆的方程.
(1)若圆经过点,且圆心与点关于直线对称,求圆标准方程;
(2)若圆与直线和直线都相切,且圆心在x轴上,求圆的标准方程.
20. 已知四棱锥,底面是边长为2的菱形,平面,且,,,分别是,的中点.
(1)求与平面所成角的正弦值;
(2)求二面角的正切值;
(3)求点到平面的距离.
21. 将一块直角三角形木板置于平面直角坐标系中,已知,点是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分钻掉,可用经过点的任一直线将三角形木板钻成设直线的斜率为
(1)求点的坐标(用表示)及直线的斜率的范围;
(2)令的面积为,试求出的取值范围.
22. 某校积极开展社团活动,在一次社团活动过程中,一个数学兴趣小组发现《九章算术》中提到了“刍薨”这个五面体,于是他们仿照该模型设计了一道数学探究题,如图1,E、F、G分别是边长为4的正方形的三边的中点,先沿着虚线段将等腰直角三角形裁掉,再将剩下的五边形沿着线段EF折起,连接就得到了一个“刍甍” (如图2)。
(1)若O是四边形对角线的交点,求证:平面;
(2)若二面角的大小为求平面与平面夹角的余弦值.
2023—2024学年度上学期东北育才超常教育实验部
少儿35班数学学科阶段检测(一)
考试时间:120分钟试卷满分:150分
一.选择题(共8小题)
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】B
【4题答案】
【答案】D
【5题答案】
【答案】A
【6题答案】
【答案】D
【7题答案】
【答案】B
【8题答案】
【答案】A
二.多选题(共4小题)
【9题答案】
【答案】AB
【10题答案】
【答案】BCD
【11题答案】
【答案】CD
【12题答案】
【答案】BC
三.填空题(共4小题)
【13题答案】
【答案】或
【14题答案】
【答案】或
【15题答案】
【答案】
【16题答案】
【答案】
四.解答题(共6小题)
【17题答案】
【答案】(1);;
(2)或.
【18题答案】
【答案】(1),,
(2)
【19题答案】
【答案】(1);
(2).
【20题答案】
【答案】(1)
(2)2 (3)
【21题答案】
【答案】(1),;(2).
【22题答案】
【答案】(1)证明见解析;
(2).
相关试卷
这是一份辽宁省重点高中沈阳市郊联体2023_2024学年高二数学上学期10月月考试题扫描版,共10页。试卷主要包含了单项选择题,多选题,填空题等内容,欢迎下载使用。
这是一份辽宁省沈阳市2023_2024学年高一数学上学期10月月考试题含解析,共15页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
这是一份辽宁省滨城高中联盟2023_2024学年高二数学上学期10月月考试题,共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












