广西名校2024-2025学年高三上学期9月联合调研测试 数学科试卷（含解析）

这是一份广西名校2024-2025学年高三上学期9月联合调研测试 数学科试卷（含解析），共18页。试卷主要包含了已知，则，设等比数列的前n项和为，，，则，已知点P在抛物线M，根据公式，的值所在的区间是，已知函数，则下列说法中正确的是等内容，欢迎下载使用。

数学科试卷
试卷满分：150分 考试时间：120分钟
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上.
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.
3．考试结束后，将本试卷和答题卡一并交回.
一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.
1．设集合，，若，则（ ）
A．B．1C．2D．3
2．若复数z是方程的一个根，则（ ）
A．3B．C．5D．
3．在平行四边形ABCD中，，，，，则（ ）
A．1B．C．2D．3
4．已知，则（ ）
A．B．C．D．
5．设等比数列的前n项和为，，，则（ ）
A．B．63C．D．31
6．已知，，，则a，b，c的大小关系是（ ）
A．B．C．D．
7．已知点P在抛物线M：上，过点P作圆C：的切线，若切线长为，则点P到M的准线的距离为（ ）
A．5B．C．6D．
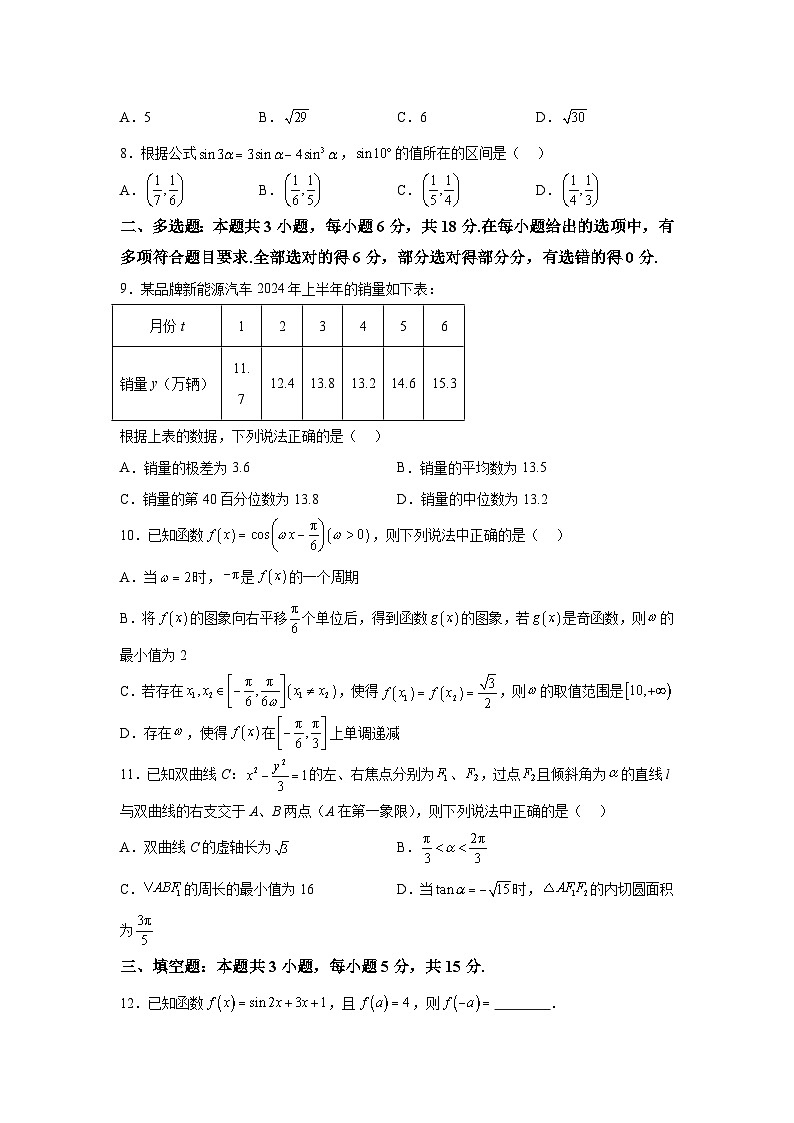
8．根据公式，的值所在的区间是（ ）
A．B．C．D．
二、多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对得部分分，有选错的得0分.
9．某品牌新能源汽车2024年上半年的销量如下表：
根据上表的数据，下列说法正确的是（ ）
A．销量的极差为3.6B．销量的平均数为13.5
C．销量的第40百分位数为13.8D．销量的中位数为13.2
10．已知函数，则下列说法中正确的是（ ）
A．当时，是的一个周期
B．将的图象向右平移个单位后，得到函数的图象，若是奇函数，则的最小值为2
C．若存在，使得，则的取值范围是
D．存在，使得在上单调递减
11．已知双曲线C：的左、右焦点分别为、，过点且倾斜角为的直线l与双曲线的右支交于A、B两点（A在第一象限），则下列说法中正确的是（ ）
A．双曲线C的虚轴长为B．
C．的周长的最小值为16D．当时，的内切圆面积为
三、填空题：本题共3小题，每小题5分，共15分.
12．已知函数，且，则 ．
13．将一个底面半径为，高为的圆柱形铁块熔铸成一个实心铁球，则该实心铁球的表面积为 ．
14．已知有，两个盒子，其中盒中有3个黑球和3个白球，盒中有3个黑球和2个白球，这些球除颜色外完全相同.甲从盒，乙从盒各随机抽取一个球，若两球同色，则甲胜，并将取出的2个球全部放入盒中，若两球不同色，则乙胜，并将取出的2个球全部放入盒中.按上述方法重复操作两次后，盒中有8个球的概率是 ．
四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.
15．记的内角A，B，C的对边分别为a，b，c，面积为S，已知．
(1)求的大小；
(2)若，E是AC的中点，且，求BE．
16．某高新技术企业新研发出了一种产品，该产品由三个电子元件组装而成，这三个电子元件在生产过程中的次品率均为.组装过程中不会造成电子元件的损坏，当且仅当三个电子元件都不是次品时，产品能正常工作，否则该产品为次品.
(1)设一件产品中所含电子元件为次品的个数为X，求X的分布列和期望；
(2)设“任取一件产品为次品”，“该产品仅有一个电子元件是次品”，求；
(3)安排质检员对这批产品进行逐一检查，确保没有次品流入市场.现有两种方案，
方案一：安排三个质检员先行检测这三个元件，次品不进入组装生产线；
方案二：安排一个质检员检测成品，若发现次品，则进行电子元件的更换，保证产品能正常工作.更换电子元件的费用为15元/个．
已知每位质检员的月工资为3000元，该企业每月生产该产品800件，请从企业获益的角度考虑，应该选择哪种方案？
17．如图，在四棱锥中，平面底面，，底面是边长为的正方形．
(1)求证：；
(2)E是棱PA上一点，若AC与平面所成角为，求四棱锥的体积．
18．椭圆E：的离心率为，过点的直线l与椭圆E交于M，N两点．当直线l过坐标原点O时，．
(1)求椭圆E的方程．
(2)设A，B分别是椭圆E的右顶点和上顶点，过点M作x轴的平行线分别与直线AB，NB交于C，D两点．试探究D，C，M三点的横坐标是否构成等差数列，并说明理由．
19．已知函数，且x轴是曲线的切线，
(1)求的最小值；
(2)证明：；
(3)设，，证明：对任意，．
月份t
1
2
3
4
5
6
销量y（万辆）
11.7
12.4
13.8
13.2
14.6
15.3
1．B
【分析】根据子集关系，分别讨论和，并检验集合元素的互异性即可得结果．
【详解】由已知得，若，解得，此时,，,1,，成立；
若，解得，此时,，,,，不成立；
若，解得，此时,，,3,，不成立；
综上所述：．
故选：B．
2．D
【分析】首先设，，代入方程得到，即可得到答案.
【详解】设，，
所以.
所以.
所以.
故选：D
3．A
【分析】根据题意将向量转化为以向量为基底的表示形式，再利用平面向量数量积的定义可得结果.
【详解】如下图所示：
由可得；
所以
.
故选：A.
4．C
【分析】首先根据诱导公式得到，从而得到，再利用余弦二倍角和同角三角函数关系求解即可.
【详解】，
所以，
所以.
所以.
故选：C
5．C
【分析】利用等比数列的通项公式、求和公式即可得出．
【详解】设等比数列的公比为，
，，
，
解：，
，
解得：，
则，
故选：C．
6．A
【分析】通过换底公式得，再结合单调性可以判断b，c的大小，再以“1”作为中间量，可以判断a，b的大小，从而得解.
【详解】设，，则，当且仅当时等号成立，则，
又，，所以
因为，所以，
综上，a，b，c的大小关系是
故选：A
7．C
【分析】根据点P的位置以及切线长可解得点横坐标为5，再由焦半径公式可得结果.
【详解】设点，由圆的方程可知圆心，半径；
又切线长为，可得，
即，解得，可得；
再由抛物线定义可得点P到M的准线的距离为.
故选：C
8．B
【分析】根据已知条件构造函数，对其求导，结合导数分析函数的单调性，再由函数零点的存在性定理判断即可.
【详解】因为，
设，则，
所以，
所以当时，f'x<0，
所以在上单调递减且，
因为，，结合各选项，
由零点存在性定理可知.
故选：.
【点睛】方法点睛：解决本题的关键是根据已知条件构造函数，根据导数与单调性的关系即零点存在定理解题.
9．AB
【分析】根据极差的概念，百分位数的概念，平均数与中位数的概念，即可分别求解．
【详解】解：A．根据表格数据可得销量的极差为，选项正确；
B．根据表格数据可得销量的平均数为，选项正确；
C．，销量的第40百分位数是从小到大排列的第3个数据，即为13.2，故选项错误；
D．中位数为，故选项错误；
故选：AB．
10．ABC
【分析】由的单调性，奇偶性，周期性逐项判断.
【详解】对于A:当时，，所以最小正周期为，所以是的一个周期，正确；
对于B：将将的图象向右平移个单位后得到
因为是奇函数，所以，解得,
当时，最小此时为2，正确；
对于C：因为，当时，，
当时，
又存在，使得，
所以当时，，解得：，正确；
对于D: 存在，若在上单调递减，
由复合函数的单调性可得：
因为，所以，故
可得：解得：，因为，，则必有，
所以同时满足的必然小于0，这与矛盾，错误.
故选:ABC
11．BCD
【分析】根据双曲线的虚轴定义及b判断A,根据渐近线斜率及倾斜角判断进而判断B,联立方程组得出弦长最小值为通径，结合定义得出周长最小值判断C, 根据的周长及面积计算的内切圆半径为r判断D.
【详解】
对于A:因为，所以虚轴长为，A错误；
对于B:因为双曲线渐近线方程为，倾斜角为，
过点且倾斜角为的直线l与双曲线的右支交于A、B两点,得出B正确；
对于C: 的周长为,
结合双曲线的定义，
设双曲线的右焦点为，，
当直线AB斜率不存在时，直线AB的方程为，则
当直线AB斜率存在时，设直线AB的方程为
联立，消去，得，
又，故或,
而
，
所以当直线AB与x轴垂直时，的长最小，即最小值为，的周长最小值为，故C正确；
对于D: 当时, 设直线AB的方程为
联立，消去，得，
，当时,A点坐标 ，
，
的周长，
设的内切圆半径为r，则，解得，
因此的内切圆面积为，D正确.
故选：BCD.
12．
【分析】构造奇函数，即可求解.
【详解】令，
所以为奇函数，
所以
所以
所以
故答案为：
13．
【分析】先利用体积相等求出，进而可求其表面积.
【详解】设实心铁球的半径为，
由题意可知，得，
故实心铁球的表面积为，
故答案为：
14．
【分析】确定两次取球后盒中有8个球必须是满足两次取球均为甲获胜，再分别计算出第一次都取黑球，第二次取同色球，第一次都取白球，第二次取同色球的概率，相加即可求解.
【详解】若两次取球后，盒中有8个球，则两次取球均为甲获胜，
第一次取球甲乙都取到黑球，其概率为，
第一次取球后盒中有4个黑球和3个白球，盒中有2个黑球和2个白球，
第二次取到同色球的概率为，
此时盒中有8个球的概率为；
若第一次取球甲乙都取到白球，其概率为，
第一次取球后盒中有3个黑球和4个白球，盒中有3个黑球和1个白球，
第二次取到同色球的概率为，
此时盒中有8个球的概率为；
所以盒中有8个球的概率为.
故答案为：.
【点睛】关键点点睛：本题的突破口在于先分清楚两次取球后，盒中有8个球，则两次取球均为甲获胜，再分别讨论并计算出第一次都取黑球，第二次取同色球，第一次都取白球，第二次取同色球的概率，相加即可求解.
15．(1)
(2)
【分析】（1）根据三角形的面积公式，结合余弦定理，可求角.
（2）先利用，得到边的关系，再用余弦定理，结合，可求的值，借助向量可求三角形中线的长度.
【详解】（1）由，
又为三角形内角，所以.
（2）如图所示：

因为为中点，所以，
因为，所以.
所以.
又，所以.
所以.
所以.
所以.
故.
16．(1)分布列见解析，；
(2)
(3)选择方案二.
【分析】（1）写出所有X的可能取值并求得对应概率即可得出分布列和期望；
（2）根据条件概率计算公式即可求得答案；
（3）依据所给方案分别计算出两种方案每月所需支出的总费用，选择较小的即可.
【详解】（1）根据题意可得X的所有可能取值为，
易知，；
，；
所以X的分布列如下：
可得期望值为；
（2）由（1）可知，；
则.
（3）若采用方案一，则每月支出总费用为元；
若采用方案二，
由（1）可知平均每个产品需更换的电子元件个数，则每月生产的800件产品平均需更换个，
每月更换电子元件的总费用为元，
则每月支出总费用为元；
显然，
所以从企业获益的角度考虑，应该选择方案二.
17．(1)证明见解析
(2)
【分析】（1）利用面面垂直的性质定理以及线面垂直的判定定理可得平面，即可证明，可得结论；
（2）建立空间直角坐标系，利用线面角的向量求法求出点的坐标，再由锥体体积公式计算可得结果.
【详解】（1）取的交点为，连接，如下图所示：
又因为底面是正方形，所以为的中点，
又，所以，
因为平面底面，平面底面，平面，
所以平面，
又平面，所以，
因为为的中点且，
可得.
（2）由底面是边长为的正方形，所以；
由（1）可知三条直线两两垂直，以为坐标原点，分别以所在直线为轴建立空间直角坐标系，如下图所示：
易知，所以；
可得，
所以，
由E是棱PA上一点可设；
则；
设平面的一个法向量为，
则，得，令，则；
所以;
由AC与平面所成角为可得；
整理可得，解得，
因此E是棱PA的中点，即，
所以E到底面的距离即为四棱锥的高为，
因此四棱锥的体积为.
18．(1)
(2)D，C，M三点的横坐标构成等差数列，证明见解析
【分析】（1）由题意，得直线l的方程，根据直线l与椭圆相交弦长MN，求出的坐标，从而由离心率与的坐标列出等式求出和的值，进而可得椭圆的方程；
（2）设出直线的方程，将直线的方程与椭圆方程联立，将问题转化成求证，按部就班求解即可．
【详解】（1）由于离心率，所以，
当过点的直线l过坐标原点O时，直线斜率为，
则此时直线l的方程为，
设直线l与椭圆E交点，不妨取，则，且①，
因为，所以②，
由①②可得，，
所以可得，解得，
故椭圆E的方程为
（2）D，C，M三点的横坐标构成等差数列，理由如下：
不妨设直线的方程为，,，,，，
因为直线经过点，所以，
联立，消去并整理得，
由韦达定理得，，
所以，
因为，，三点共线，
所以，而，
即，则，
故，，三点的横坐标成等差数列．
19．(1)
(2)证明见解析
(3)证明见解析
【分析】（1）先根据切线方程求出，进而再利用导数求最小值；
（2）利用（1）的结论构造不等式，进而可得，再利用累加法即可证明；
（3）先分离参数后利用的最大值，将问题转化为证明，利用关系可得，进而只需证明即可，构造函数，进而利用导数求其最小值即可证明.
【详解】（1）由得，
因切线方程为，令，得，故可知切点为，
所以，得，
故，，
当x∈0,1时，f'x<0，在区间0,1上单调递减，
当x∈1,+∞时，f'x>0，在区间1,+∞上单调递增，
故的最小值为f1=0
（2）由（1）可知，故，故，
令，，则，即，即，
故，
即，即证
（3）由题意，
由得①，
要证明对任意，，只需要，
令，，，
令，，
在区间上单调递增，故，故，
故在上递增，故只需证明，
由①可知，
由（1）可知，故，
只需证明，化简为成立即可，
令，则，
在区间上单调递增，故，所以得证.
【点睛】关键点点睛：本题第三问处理的关键是：对目标式分离参数，转化为求解的最大值，结合关系，消去参数后，构造函数，进而利用导数求其最小值即可证明.
X
0
1
2
3