浙江省绍兴市诸暨市2024年数学九上开学调研模拟试题【含答案】

这是一份浙江省绍兴市诸暨市2024年数学九上开学调研模拟试题【含答案】，共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）1.在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）
A．B．C．D．
2、（4分）下列因式分解正确的是（ ）
A．B．
C．D．
3、（4分）下列图形中，可以抽象为中心对称图形的是（ ）
A．B．
C．D．
4、（4分）若分式有意义，则的取值范围是（ ）
A．B．C．D．
5、（4分）下列根式中是最简二次根式的是
A．B．C．D．
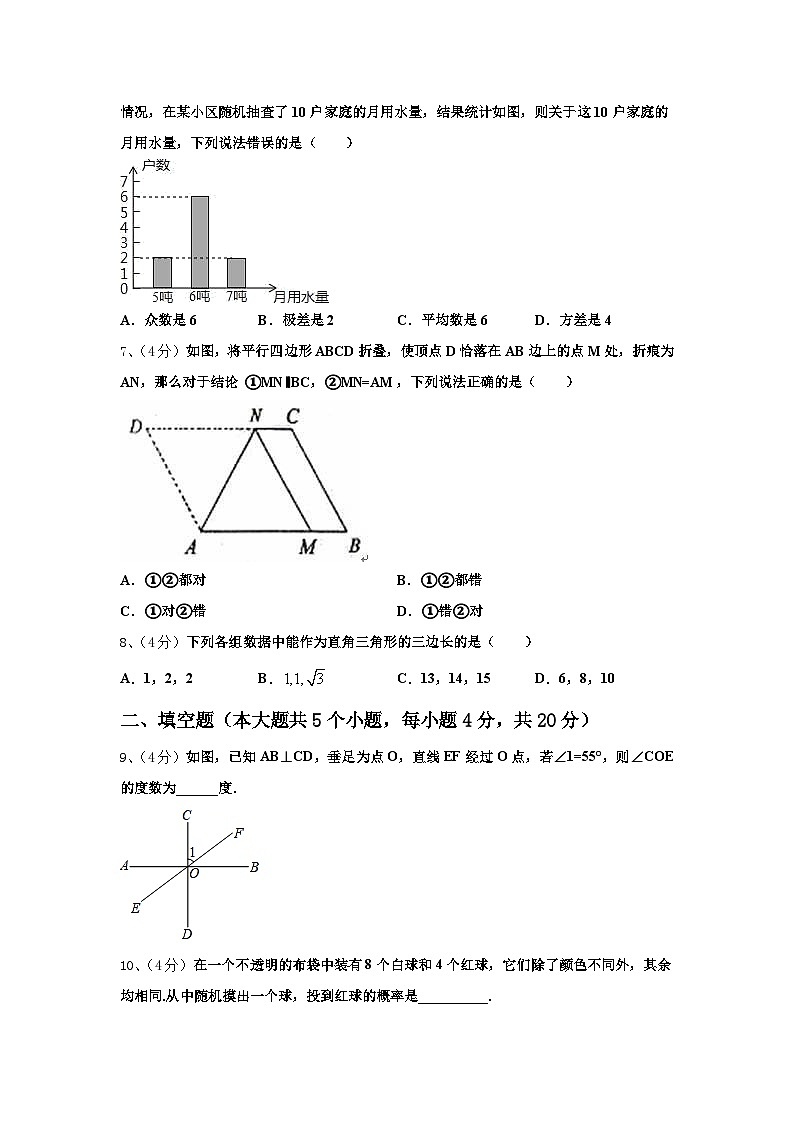
6、（4分）2013年，某市发生了严重干旱，该市政府号召居民节约用水，为了解居民用水情况，在某小区随机抽查了10户家庭的月用水量，结果统计如图，则关于这10户家庭的月用水量，下列说法错误的是（ ）
A．众数是6B．极差是2C．平均数是6D．方差是4
7、（4分）如图，将平行四边形ABCD折叠，使顶点D恰落在AB边上的点M处，折痕为AN，那么对于结论 ①MN∥BC，②MN=AM，下列说法正确的是（ ）
A．①②都对B．①②都错
C．①对②错D．①错②对
8、（4分）下列各组数据中能作为直角三角形的三边长的是（ ）
A．1，2，2B．C．13，14，15D．6，8，10
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，已知AB⊥CD，垂足为点O，直线EF经过O点，若∠1=55°，则∠COE的度数为______度．
10、（4分）在一个不透明的布袋中装有8个白球和4个红球，它们除了颜色不同外，其余均相同.从中随机摸出一个球，投到红球的概率是__________.
11、（4分）直角三角形中，两条直角边长分别为12和5，则斜边上的中线长是________．
12、（4分）如图，矩形ABCD中，，，将矩形折叠，使点B与点D重合，点A的对应点为，折痕EF的长为________.
13、（4分）本市5月份某一周毎天的最高气温统计如下表：则这组数据的众数是___．
三、解答题（本大题共5个小题，共48分）
14、（12分）某市建设全长540米的绿化带，有甲、乙两个工程队参加．甲队平均每天绿化的长度是乙队的1.5倍．若由一个工程队单独完成绿化，乙队比甲队对多用6天，分别求出甲、乙两队平均每天绿化的长度。
15、（8分）如图，已知菱形ABCD边长为4，，点E从点A出发沿着AD、DC方向运动，同时点F从点D出发以相同的速度沿着DC、CB的方向运动．
如图1，当点E在AD上时，连接BE、BF，试探究BE与BF的数量关系，并证明你的结论；
在的前提下，求EF的最小值和此时的面积；
当点E运动到DC边上时，如图2，连接BE、DF，交点为点M，连接AM，则大小是否变化？请说明理由．
16、（8分）如图，△ABC中，CD⊥AB于D，若AD＝2BD，AC＝3，BC＝2，求BD的长．
17、（10分）先分解因式，再求值：，其中，．
18、（10分）如图，在平面直角坐标系中，一次函数y=kx+b的图象经过点A（﹣2，6），且与x轴相交于点B，与正比例函数y=3x的图象相交于点C，点C的横坐标为1．
（1）求k、b的值；
（2）若点D在y轴负半轴上，且满足S△COD=S△BOC，求点D的坐标．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，矩形OABC中，D为对角线AC，OB的交点，直线AC的解析式为，点P是y轴上一动点，当的周长最小时，线段OP的长为______．
20、（4分）若解分式方程产生增根，则m＝_____．
21、（4分）已知函数y=2x2-3x+l，当y=1时，x=_____.
22、（4分）关于的方程有实数根,则的取值范围是_________.
23、（4分）如图，对面积为S的△ABC逐次进行以下操作：第一次操作，分别延长AB、BC、CA至点A1、B1、C1，使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1、B1、C1，得到△A1B1C1，记其面积为S1；第二次操作，分别延长A1B1、B1C1、C1A1至点A2、B2、C2，使得A2B1=2A1B1，B2C1=2B1C1，C2A1=2C1A1，顺次连接A2、B2、C2，得到△A2B2C2，记其面积为S2；··· ；则______．按此规律继续下去，可得到，则其面积_______．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在直角梯形ABCD中，AD∥BC，∠B=90°，且AD=12cm，AB=8cm，DC=10cm，若动点P从A点出发，以每秒2cm的速度沿线段AD向点D运动；动点Q从C点出发以每秒3cm的速度沿CB向B点运动，当P点到达D点时，动点P、Q同时停止运动，设点P、Q同时出发，并运动了t秒，回答下列问题：
（1）BC= cm；
（2）当t为多少时，四边形PQCD成为平行四边形？
（3）当t为多少时，四边形PQCD为等腰梯形？
（4）是否存在t，使得△DQC是等腰三角形？若存在，请求出t的值；若不存在，说明理由．
25、（10分）某商店准备进一批季节性小家电，单价40元．经市场预测，销售定价为52元时，可售出180个，定价每增加1元，销售量净减少10个；定价每减少1元，销售量净增加10个．因受库存的影响，每批次进货个数不得超过180个，商店若将准备获利2000元，则应进货多少个？定价为多少元？
26、（12分）已知边长为4的正方形ABCD，顶点A与坐标原点重合，一反比例函数图象过顶点C，动点P以每秒1个单位速度从点A出发沿AB方向运动，动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC﹣CB﹣BA方向顺时针折线运动，当点P与点Q相遇时停止运动，设点P的运动时间为t．
（1）求出该反比例函数解析式；
（2）连接PD，当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时，求点Q的坐标；
（3）用含t的代数式表示以点Q、P、D为顶点的三角形的面积s，并指出相应t的取值．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
根据轴对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．
【详解】
A、不是轴对称图形，故A不符合题意；
B、不是轴对称图形，故B不符合题意；
C、不是轴对称图形，故C不符合题意；
D、是轴对称图形，故D符合题意．
故选D.
本题主要考查轴对称图形的知识点．确定轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2、C
【解析】
根据因式分解的定义及方法逐项分析即可.
【详解】
A. ，故不正确；
B. 在实数范围内不能因式分解，故不正确；
C. ，正确；
D. 的右边不是积的形式，故不正确；
故选C.
本题考查了因式分解，把一个多项式化成几个整式的乘积的形式，叫做因式分解.因式分解常用的方法有：①提公因式法；②公式法；③十字相乘法；④分组分解法. 因式分解必须分解到每个因式都不能再分解为止.
3、B
【解析】
根据中心对称图形的概念求解．
【详解】
A. 不是中心对称图形，因为找不到任何这样的一点，旋转180度后它的两部分能够重合；即不满足中心对称图形的定义，故此选项错误；
B. 是中心对称图形，故此选项正确；
C. 不是中心对称图形，因为找不到任何这样的一点，旋转180度后它的两部分能够重合；即不满足中心对称图形的定义，故此选项错误；
D. 不是中心对称图形，因为找不到任何这样的一点，旋转180度后它的两部分能够重合；即不满足中心对称图形的定义，故此选项错误。
故选：B.
此题考查中心对称图形，难度不大.
4、A
【解析】
根据分式有意义的条件，得到关于x的不等式，进而即可求解．
【详解】
∵分式有意义，
∴，即：，
故选A．
本题主要考查分式有意义的条件，掌握分式的分母不等于零，是解题的关键．
5、B
【解析】
A．=，故此选项错误；
B．是最简二次根式，故此选项正确；
C．=3，故此选项错误；
D．=，故此选项错误；
故选B．
考点：最简二次根式．
6、D
【解析】
众数是一组数据中出现次数最多的数，极差是数据中最大的与最小的数据的差，平均数是所有数据的和除以数据的个数，分别根据以上定义可分别求出众数，极差和平均数，然后根据方差的计算公式进行计算求出方差，即可得到答案．
【详解】
解：这组数据6出现了6次，最多，所以这组数据的众数为6；
这组数据的最大值为7，最小值为5，所以这组数据的极差＝7﹣5＝2；
这组数据的平均数＝（5×2+6×6+7×2）＝6；
这组数据的方差S2＝ [2•（5﹣6）2+6•（6﹣6）2+2•（7﹣6）2]＝0.4；
所以四个选项中，A、B、C正确，D错误．
故选：D．
本题考查了方差的定义和意义：数据x1，x2，…xn，其平均数为，则其方差S2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]；方差反映了一组数据在其平均数的左右的波动大小，方差越大，波动越大，越不稳定；方差越小，波动越小，越稳定．也考查了平均数和众数以及极差的概念．
7、A
【解析】
根据题意得到四边形AMND为菱形，故可判断．
【详解】
解：∵四边形ABCD平行四边形，
∴∠B=∠D=∠AMN，
∴MN∥BC，
∵AM=DA，
∴四边形AMND为菱形，
∴MN=AM．
故①②正确．
故选A．
8、D
【解析】
根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形判定则可．
【详解】
解：A、，不能构成直角三角形，故不符合题意；
B、，不能构成直角三角形，故不符合题意；
C、，不能构成直角三角形，故不符合题意；
D、，能构成直角三角形，故符合题意．
故选：D．
本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1
【解析】
根据邻补角的和是180°，结合已知条件可求∠COE的度数．
【详解】
∵∠1=55°，
∴∠COE=180°-55°=1°．
故答案为1．
此题考查了垂线以及邻补角定义，关键熟悉邻补角的和是180°这一要点．
10、
【解析】
由在一个不透明的布袋中装有8个白球和4个红球，它们除了颜色不同外，其余均相同，直接利用概率公式求解即可求得答案．
【详解】
∵在一个不透明的布袋中装有8个白球和4个红球，它们除了颜色不同外，其余均相同．
∴从中随机摸出一个球，摸到红球的概率是：
故答案为：
此题考查概率公式，掌握运算法则是解题关键
11、6.5
【解析】
利用勾股定理求得直角三角形的斜边，然后利用直角三角形斜边上的中线等于斜边的一半解题．
【详解】
解：如图，在△ABC中，∠C=90°，AC=11，BC=5，
根据勾股定理知，
∵CD为斜边AB上的中线，
故答案为：6.5
本题考查了勾股定理、直角三角形斜边上的中线．勾股定理：如果直角三角形两直角边分别为a，b，斜边为c，那么a1+b1=c1．即直角三角形，两直角边的平方和等于斜边的平方．直角三角形的性质：在直角三角形中斜边上的中线等于斜边的一半．
12、
【解析】
过点F作FH⊥AD于H，先利用矩形的性质及轴对称的性质证明DE=DF=BF，在Rt△DCF中通过勾股定理求出DF的长，再求出HE的长，再在Rt△HFE中利用勾股定理即可求出EF的长．
【详解】
解：如图，过点F作FH⊥AD于H，

∵四边形ABCD为矩形，
∴BC∥AD，∠C=90°，DC=AB=4，四边形DCFH为矩形，
∴∠BFE=∠DEF，
由折叠可知，∠BFE=∠DFE，BF=DF，
∴∠DEF=∠DFE，
∴DE=DF=BF，
在Rt△DCF中
设DF=x，则CF=BC-BF=6-x，
∵DC2+CF2=DF2，
∴42+（6-x）2=x2，
解得，x=，
∴DE=DF=BF=，
∴CF=BC-BF=6-=，
∵四边形DCFH为矩形，
∴HF=CD=4，DH=CF=，
∴HE=DE-DH=，
∴在Rt△HFE中，
故答案为
本题考查了矩形的性质，轴对称的性质，勾股定理等，解题关键是能够灵活运用矩形的性质及轴对称的性质．
13、1．
【解析】
根据众数的定义来判断即可，众数：一组数据中出现次数最多的数据叫做众数.
【详解】
解：数据1出现了3次，次数最多，所以这组数据的众数是1．
故答案为：1．
众数的定义是本题的考点，属于基础题型，熟练掌握众数的定义是解题的关键.
三、解答题（本大题共5个小题，共48分）
14、甲队平均每天绿化45米，乙队平均每天绿化30米
【解析】
设乙队平均每天绿化x米， 由时间=工作量÷工作效率，结合乙队比甲队多用6天列分式方程，解出x, 再代入方程检验即可求出x, 则乙队平均每天绿化多少米也可求.
【详解】
设乙队平均每天绿化x米，则甲队平均每天绿化1.5x米，
依题意得
解得x=30
经检验x=30是原方程的根且符合题意，
∴1.5x=45(米)，
答：甲队平均每天绿化45米，乙队平均每天绿化30米。
此题主要考查分式方程的应用，解题的关键是根据题意找到等量关系列方程.
15、，证明见解析；的最小值是，；如图3，当点E运动到DC边上时，大小不发生变化，理由见解析.
【解析】
先证明和是等边三角形，再证明≌，可得结论；
由≌，易证得是正三角形，继而可得当动点E运动到当，即E为AD的中点时，BE的最小，根据等边三角形三线合一的性质可得BE和EF的长，并求此时的面积；
同理得：≌，则可得，所以，则A、B、M、D四点共圆，可得．
【详解】
，
证明：、F的速度相同，且同时运动，
，
又四边形ABCD是菱形，
，
，
，
是等边三角形，
同理也是等边三角形，
，
在和中，
，
≌，
；
由得：≌，
，
，
，
是等边三角形，
，
如图2，当动点E运动到，即E为AD的中点时，BE的最小，此时EF最小，
，，
，
的最小值是，
中，，，
，
，
；
如图3，当点E运动到DC边上时，大小不发生变化，
在和中，
，
≌，
，
，
，
，
，
，
、B、M、D四点共圆，
．
此题是四边形的综合题，考查了菱形的性质、等边三角形的判定与性质、四点共圆的判定和性质、垂线段最短以及全等三角形的判定与性质注意证得≌是解此题的关键．
16、．
【解析】
试题分析：因为CD⊥AB，所以△ACD和△BCD都是直角三角形，都利用勾股定理表示CD的长，得到方程即可求解．
试题解析：根据题意CD2=AC2-AD2=32-（2BD）2=9-4BD2，
CD2=BC2-BD2=22-BD2=4-BD2，
∴9-4BD2=4-BD2，
解得BD2=，
∴BD=．
考点：勾股定理．
17、，1
【解析】
先提取公因式，再利用完全平方公式进行因式分解，将，代入求解即可．
【详解】
解：
＝
＝
∵其中，
∴原式

＝1．
本题考查了因式分解的问题，掌握完全平方公式是解题的关键．
18、（1）k=-1，b=4；（2）点D的坐标为（0，-4）．
【解析】
分析：（1）利用一次函数图象上点的坐标特征可求出点C的坐标，根据点A、C的坐标，利用待定系数法即可求出k、b的值；
（2）利用一次函数图象上点的坐标特征可求出点B的坐标，设点D的坐标为（0，m）（m＜0），根据三角形的面积公式结合S△COD=S△BOC，即可得出关于m的一元一次方程，解之即可得出m的值，进而可得出点D的坐标．
详解：（1）当x=1时，y=3x=3，
∴点C的坐标为（1，3）．
将A（﹣2，6）、C（1，3）代入y=kx+b，
得：，
解得：．
（2）当y=0时，有﹣x+4=0，
解得：x=4，
∴点B的坐标为（4，0）．
设点D的坐标为（0，m）（m＜0），
∵S△COD=S△BOC，即﹣m=××4×3，
解得：m=-4，
∴点D的坐标为（0，-4）．
点睛：本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征、待定系数法求一次函数解析式以及三角形的面积，解题的关键是：（1）根据点的坐标，利用待定系数法求出k、b的值；（2）利用三角形的面积公式结合结合S△COD=S△BOC，找出关于m的一元一次方程．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
根据题意可以得到点A、B、C的坐标和点D的坐标，然后最短路径问题可以求得点P的坐标，从而可以求得OP的长．
【详解】
解：作点D关于y轴的对称点，连接交y轴于点P，则点P即为所求，
直线AC的解析式为，
当时，，当时，，
点A的坐标为，点C的坐标为，
点D的坐标为，点B的坐标为，
点的坐标为，
设过点B和点的直线解析式为，
，
解得，，
过点B和点的直线解析式为，
当时，，
即点P的坐标为，
.
故答案为．
本题考查一次函数的性质、矩形的性质、最短路线问题，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
20、-5
【解析】
试题分析：根据分式方程增根的产生的条件，可知x+4=0，解得x=-4，然后把分式方程化为整式方程x-1=m，解得m=-5
故答案为-5.
21、0或
【解析】
把y=1时代入解析式，即可求解．
【详解】
解：当y=1时，则1=2x2-3x+1，
解得：x=0或x=，
故答案为0或.
本题考查的是二次函数图象上的点坐标特征，只要把y值代入函数表达式求解即可．
22、k≤2
【解析】
当k-1=0时，解一元一次方程可得出方程有解；当k-1≠0时，利用根的判别式△=16-2k≥0，即可求出k的取值范围．综上即可得出结论．
【详解】
当k-1=0，即k=1时，方程为2x+1=0，
解得x=-，符合题意；
②当k-1≠0，即k≠1时，△=22-2（k-1）=16-2k≥0，
解得：k≤2且k≠1．
综上即可得出k的取值范围为k≤2．
故答案为k≤2．
本题考查了根的判别式，分二次项系数为零和非零两种情况考虑是解题的关键．
23、19S
【解析】
首先根据题意，求得，同理求得，则可求得面积的值；根据题意发现规律：即可求得答案．
【详解】
连，
∵，
∴，
同理：，
∴，
同理：，
∴，
即，
同理：S，S，
∴．
故答案是：19S，．
本题主要考查了三角形面积及等积变换，利用三角形同高则面积比与底边关系分别分析得出规律：是解题关键．
二、解答题（本大题共3个小题，共30分）
24、（1）18cm（2）当t=秒时四边形PQCD为平行四边形（3）当t=时，四边形PQCD为等腰梯形（4）存在t，t的值为秒或4秒或秒
【解析】试题分析：（1）作DE⊥BC于E，则四边形ABED为矩形．在直角△CDE中，已知DC、DE的长，根据勾股定理可以计算EC的长度，根据BC=BE+EC即可求出BC的长度；
（2）由于PD∥QC，所以当PD=QC时，四边形PQCD为平行四边形，根据PD=QC列出关于t的方程，解方程即可；
（3）首先过D作DE⊥BC于E，可求得EC的长，又由当PQ=CD时，四边形PQCD为等腰梯形，可求得当QC-PD=QC-EF=QF+EC=2CE，即3t-（12-2t）=12时，四边形PQCD为等腰梯形，解此方程即可求得答案；
（4）因为三边中，每两条边都有相等的可能，所以应考虑三种情况．结合路程=速度×时间求得其中的有关的边，运用等腰三角形的性质和解直角三角形的知识求解．
试题解析：根据题意得：PA=2t，CQ=3t，则PD=AD-PA=12-2t．
（1）如图，过D点作DE⊥BC于E，则四边形ABED为矩形，
DE=AB=8cm，AD=BE=12cm，
在直角△CDE中，∵∠CED=90°，DC=10cm，DE=8cm，
∴EC==6cm，
∴BC=BE+EC=18cm．
（2）∵AD∥BC，即PD∥CQ，
∴当PD=CQ时，四边形PQCD为平行四边形，
即12-2t=3t，
解得t=秒，
故当t=秒时四边形PQCD为平行四边形；
（3）如图，过D点作DE⊥BC于E，则四边形ABED为矩形，DE=AB=8cm，AD=BE=12cm，
当PQ=CD时，四边形PQCD为等腰梯形．
过点P作PF⊥BC于点F，过点D作DE⊥BC于点E，则四边形PDEF是矩形，EF=PD=12-2t，PF=DE．
在Rt△PQF和Rt△CDE中，
，
∴Rt△PQF≌Rt△CDE（HL），
∴QF=CE，
∴QC-PD=QC-EF=QF+EC=2CE，
即3t-（12-2t）=12，
解得：t=，
即当t=时，四边形PQCD为等腰梯形；
（4）△DQC是等腰三角形时，分三种情况讨论：
①当QC=DC时，即3t=10，
∴t=；
②当DQ=DC时，
∴t=4；
③当QD=QC时，3t×
∴t=．
故存在t，使得△DQC是等腰三角形，此时t的值为秒或4秒或秒．
考点：四边形综合题．
25、该商品每个定价为1元，进货100个.
【解析】
利用销售利润=售价﹣进价，根据题中条件可以列出利润与x的关系式，求出即可．
解：设每个商品的定价是x元，
由题意，得（x﹣40）[180﹣10（x﹣52）]=2000，
整理，得x2﹣110x+3000=0，
解得x1=50，x2=1．
当x=50时，进货180﹣10（50﹣52）=200个＞180个，不符合题意，舍去；
当x=1时，进货180﹣10（1﹣52）=100个＜180个，符合题意．
答：当该商品每个定价为1元时，进货100个．
26、（1）y=；
（2）Q1（，4）；Q2（4，），Q3（4，）；
（3）s1=8t（0＜t≤1）；s2=﹣2t2+2t+8（1≤t≤2）；s3=﹣10t+1（2≤t≤）．
【解析】
试题分析：（1）根据正方形ABCD的边长为4，可得C的坐标为（4，4），再用待定系数法求出反比例函数解析式；
（2）分点Q在CD，BC，AB边上，根据全等三角形的判定和性质求得点Q的坐标；
（3）分点Q在CD，BC，AB边上，由三角形面积公式和组合图形的面积计算即可求解．
试题解析：解：（1）∵正方形ABCD的边长为4，
∴C的坐标为（4，4），
设反比例解析式为y=，
将C的坐标代入解析式得：k=16，则反比例解析式为y=；
（2）当Q在DC上时，如图所示：
此时△APD≌△CQB，
∴AP=CQ，即t=4﹣4t，解得t=，
则DQ=4t=，即Q1（，4）；
当Q在BC边上时，有两个位置，如图所示：
若Q在上边，则△QCD≌△PAD，
∴AP=QC，即4t﹣4=t，解得t=，
则QB=8﹣4t=，此时Q2（4，）；
若Q在下边，则△APD≌△BQA，
则AP=BQ，即8﹣4t=t，解得t=，
则QB=，即Q3（4，）；
当Q在AB边上时，如图所示：
此时△APD≌△QBC，
∴AP=BQ，即4t﹣8=t，解得t=，
因为0≤t≤，所以舍去．
综上所述Q1（，4）； Q2（4，），Q3（4，）；
（3）当0＜t≤1时，Q在DC上，DQ=4t，则s=×4t×4=8t；
当1≤t≤2时，Q在BC上，则BP=4﹣t，CQ=4t﹣4，AP=t，
则s=S正方形ABCD﹣S△APD﹣S△BPQ﹣S△CDQ=16﹣AP•AD﹣PB•BQ﹣DC•CQ=16﹣t×4﹣（4﹣t）•[4﹣（4t﹣4）]﹣×4（4t﹣4）═﹣2t2+2t+8；
当2≤t≤时，Q在AB上，PQ=12﹣5t，则s=×4×（12﹣5t），即s=﹣10t+1．
总之，s1=8t（0＜t≤1）；
s2=﹣2t2+2t+8（1≤t≤2）；
s3=﹣10t+1（2≤t≤）．
考点：反比例函数综合题．
题号
一
二
三
四
五
总分
得分
批阅人
温度/℃
22
24
26
29
天数
2
1
3
1