四川省内江市名校2024-2025学年九年级数学第一学期开学学业质量监测模拟试题【含答案】

这是一份四川省内江市名校2024-2025学年九年级数学第一学期开学学业质量监测模拟试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）无论a取何值，关于x的函数y＝﹣x+a2+1的图象都不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
2、（4分）用反证法证明命题“四边形中至少有一个角不小于直角”时应假设（ ）
A．没有一个角大于直角 B．至多有一个角不小于直角
C．每一个内角都为锐角 D．至少有一个角大于直角
3、（4分）小明做了一个数学实验：将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内，看作一个容器，然后，小明对准玻璃杯口匀速注水，如图所示，在注水过程中，杯底始终紧贴鱼缸底部，则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是（ ）
A．B．
C．D．
4、（4分）下列关于直线的说法正确的是（ ）
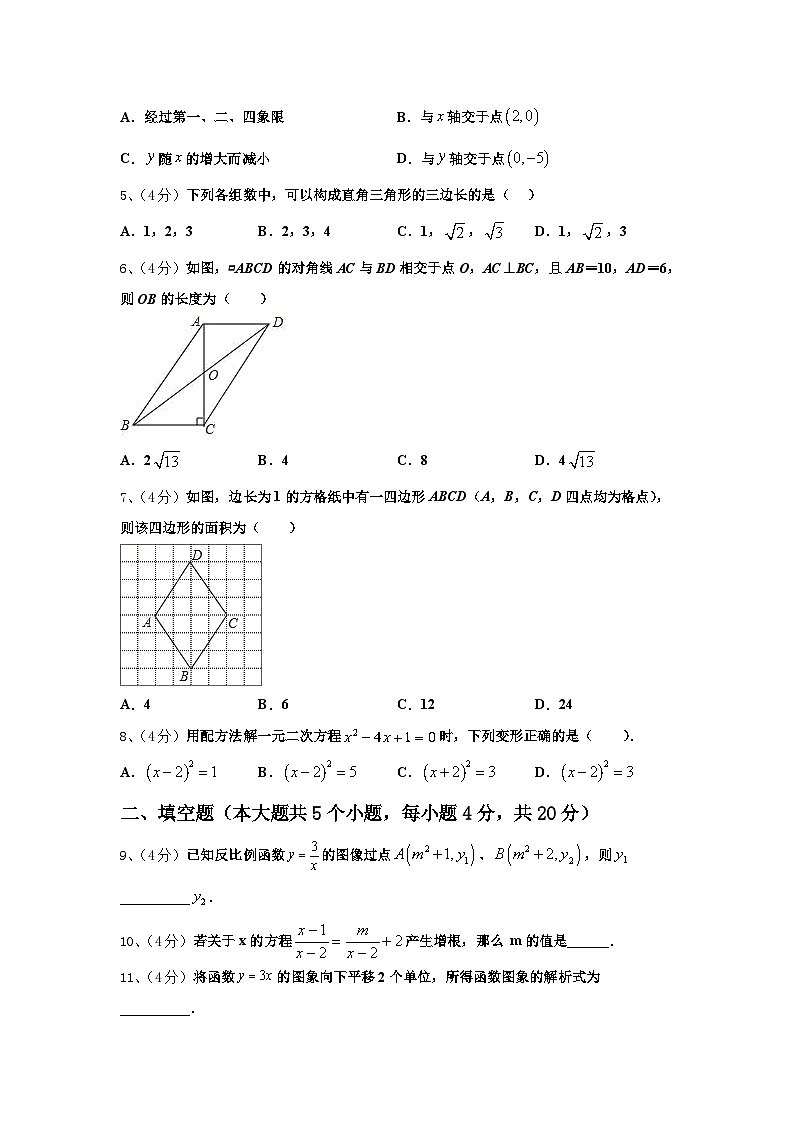
A．经过第一、二、四象限B．与轴交于点
C．随的增大而减小D．与轴交于点
5、（4分）下列各组数中，可以构成直角三角形的三边长的是（ ）
A．1，2，3B．2，3，4C．1，，D．1，，3
6、（4分）如图，▱ABCD的对角线AC与BD相交于点O，AC⊥BC，且AB＝10，AD＝6，则OB的长度为（ ）
A．2B．4C．8D．4
7、（4分）如图，边长为1的方格纸中有一四边形ABCD（A，B，C，D四点均为格点），则该四边形的面积为（ ）
A．4B．6C．12D．24
8、（4分）用配方法解一元二次方程时，下列变形正确的是（ ）．
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）已知反比例函数的图像过点、，则__________．
10、（4分）若关于x的方程产生增根，那么 m的值是______．
11、（4分）将函数的图象向下平移2个单位，所得函数图象的解析式为__________．
12、（4分）如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离AE、CF分别是1cm、2cm，则线段EF的长为 ______cm．
13、（4分）马拉松赛选手分甲、乙两组运动员进行了艰苦的训练，他们在相同条件下各10次比赛，成绩的平均数相同，方差分别为0.25，0.21，则成绩较为稳定的是_________（选填“甲”或“乙）
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，已知正方形ABCD中，以BF为底向正方形外侧作等腰直角三角形BEF，连接DF，取DF的中点G，连接EG，CG.
(1)如图1，当点A与点F重合时，猜想EG与CG的数量关系为 ，EG与CG的位置关系为 ，请证明你的结论.
(2)如图2，当点F在AB上（不与点A重合）时，（1）中结论是否仍然成立？请说明理由；如图3，点F在AB的左侧时，（1）中的结论是否仍然成立？直接做出判断，不必说明理由.
(3)在图2中，若BC=4，BF=3，连接EC，求的面积.
15、（8分）如图，要在长、宽分别为50米、40米的矩形草坪内建一个正方形的观赏亭．为方便行人，分别从东，南，西，北四个方向修四条宽度相同的矩形小路与亭子相连，若小路的宽是正方形观赏亭边长的，小路与观赏亭的面积之和占草坪面积的，求小路的宽．
16、（8分）如图，直线y=－x+4分别与x轴、y轴交于A、B两点．
（1）求A、B两点的坐标；
（2）已知点C坐标为（2,0），设点C关于直线AB的对称点为D，请直接写出点D的坐标．
17、（10分）如图，某学校有一块长为30米，宽为10米的矩形空地，计划在其中修建两块相同的矩形绿地，两块绿地之间及周边留有宽度相等的人行通道．
若设计人行通道的宽度为2米，那么修建的两块矩形绿地的面积共为多少平方米？
若要修建的两块矩形绿地的面积共为216平方米，求人行通道的宽度．
18、（10分）先化简再求值：，其中a=3.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）已知，则________．
20、（4分）如图，在平面直角坐标系中，正方形的边长为2，点的坐标为．若直线与正方形有两个公共点，则的取值范围是____________．
21、（4分）如图，四边形ABCD是正方形，以CD为边作等边三角形CDE，BE与AC相交于点M，则∠ADM的度数是_____．
22、（4分）如图，菱形ABCD的周长为16，若，E是AB的中点，则点E的坐标为_____________．
23、（4分）如图，把一张矩形的纸沿对角线BD折叠，若AD=8，AB=6，则BE=__．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，出租车是人们出行的一种便利交通工具，折线ABC是在我市乘出租车所付车费y（元）与行车里程x（km）之间的函数关系图象．
（1）根据图象，当x≥3时y为x的一次函数，请写出函数关系式；
（2）某人乘坐13km，应付多少钱？
（3）若某人付车费42元，出租车行驶了多少千米？
25、（10分）如图，在四边形中，，，，是的中点．点以每秒个单位长度的速度从点出发，沿向点运动；点同时以每秒个单位长度的速度从点出发，沿向点运动.点停止运动时，点也随之停止运动．当运动时间为多少秒时，以点，，，为顶点的四边形是平行四边形．
26、（12分）如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫做格点．
（1）以格点为顶点画，使三这长分别为；
（2）若的三边长分别为m、n、d，满足，求三边长，若能画出以格点为顶点的三角形，请画出该格点三角形．

参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据题目中的函数解析式和一次函数的性质可以解答本题．
【详解】
解：∵y＝﹣x+a2+1，k＝﹣1＜0，a2+1≥1＞0，
∴函数y＝﹣x+a2+1经过第一、二、四象限，不经过第三象限，
故选：C．
本题考查一次函数的性质，解答本题的关键是明确题意，利用一次函数的性质解答．
2、C
【解析】
至少有一个角不小于90°的反面是每个内角都为锐角，据此即可假设．
【详解】
解：反证法的第一步先假设结论不成立，即四边形的每个内角都为锐角．
故选C．
本题结合角的比较考查反证法，解答此题关键要懂得反证法的意义及步骤．在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．
3、D
【解析】
试题分析：一注水管向小玻璃杯内注水，水面在逐渐升高，当小杯中水满时，开始向大桶内流，这时最高水位高度不变，当桶水面高度与小杯一样后，再继续注水，水面高度在升高，升高的比开始慢．故选D．
考点：函数的图象．
4、D
【解析】
直接根据一次函数的性质即可解答
【详解】
A. 直线y=2x−5经过第一、三、四象限，错误；
B. 直线y=2x−5与x轴交于(,0)，错误；
C. 直线y=2x−5，y随x的增大而增大，错误；
D. 直线y=2x−5与y轴交于(0,−5)，正确
故选：D.
此题考查一次函数的性质，解题关键在于掌握其性质
5、C
【解析】
根据勾股定理的逆定理，判断三角形是否为直角三角形，需要验证三角形三边关系，两小边长的平方和等于最长边的平方即可．
【详解】
A．，不能构成直角三角形，此选项错误；
B．，不能构成直角三角形，此选项错误；
C．，能构成直角三角形，此选项正确；
D．，不能构成直角三角形，此选项错误；
故选：C．
考查了勾股定理的逆定理，利用三角形三边关系判定三角形是否为直角三角形，用到实数平方的计算，熟记定理内容，注意判定时，边长是平方关系．
6、A
【解析】
利用平行四边形的性质和勾股定理易求AC的长，进而可求出OB的长．
【详解】
∵四边形ABCD是平行四边形，
∴BC=AD=6，OA=OC，
∵AC⊥BC，AB=10，
∴，
∴，
∴；
故选：A．
本题考查了平行四边形的性质以及勾股定理的运用，熟练掌握平行四边形的性质和勾股定理是解题的关键．
7、C
【解析】
根据菱形的性质，已知AC，BD的长，然后根据菱形的面积公式可求解．
【详解】
解：由图可知，AB＝BC＝CD＝DA，
∴该四边形为菱形，
又∵AC＝4，BD＝6，
∴菱形的面积为4×6×＝1．
故选：C．
主要考查菱形的面积公式：两条对角线的积的一半，同时也考查了菱形的判定．
8、D
【解析】
根据配方法的原理，凑成完全平方式即可.
【详解】
解：
，
，
，
故选：D．
本题主要考查配方法的掌握，关键在于一次项的系数等于2倍的二次项系数和常数项的乘积.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
根据反比例函数的增减性，结合点A和点B的横坐标的大小，即可得到答案．
【详解】
∵m2≥0，
∴m2+2＞m2+1，
∵反比例函数y=，k＞0，
∴当x＞0时，y随着x的增大而减小，
∴y1＞y2，
故答案为：＞．
本题考查了反比例函数图象上点的坐标特征，正确掌握反比例函数的增减性是解题的关键．
10、1
【解析】
分式方程去分母转化为整式方程，根据分式方程有增根得到x-2=0，将x=2代入整式方程计算即可求出m的值．
【详解】
分式方程去分母得：x−1=m+2x−4，
由题意得：x−2=0，即x=2，
代入整式方程得：2−1=m+4−4，
解得：m=1.
故答案为：1.
此题考查分式方程的增根，解题关键在于掌握分式方程中增根的意义.
11、y=3x-1．
【解析】
根据“上加下减”的原则求解即可．
【详解】
将正比例函数y=3x的图象向下平移1个单位长度，所得的函数解析式为y=3x-1．
故答案为:y=3x-1．
本题考查的是一次函数的图象与几何变换，熟知函数图象变换的法则是解答此题的关键．
12、3
【解析】
∵四边形ABCD为正方形，
∴AB=BC,∠ABC=90°.
∵AE⊥l，CF⊥l，
∴∠E=∠F=90°,∠EAB+∠ABE=90°,∠FBC+∠BCF=90°.
∵∠ABE+∠ABC+∠FBC=180°，
∴∠ABE+∠FBC=90°，
∴∠EAB=∠FBC.
在△ABE和△BCF中,
，
∴△ABE≌△BCF(AAS)，
∴BE=CF=2cm，BF=AE=1cm，
∴EF=BE+BF=2+1=3cm.
故答案为3.
13、乙
【解析】
根据方差的意义判断即可．方差是用来衡量一组数据波动大小的量，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
【详解】
∵甲乙的方差分别为1．25，1．21
∴成绩比较稳定的是乙
故答案为：乙
运用了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
三、解答题（本大题共5个小题，共48分）
14、（1）EG=CG，EG⊥CG；（2）当点F在AB上（不与点A重合）时，（1）中结论仍然成立，理由见解析，点F在AB的左侧时，（1）中的结论仍然成立；（3）S△CEG=.
【解析】
（1）过E作EM⊥AD交AD的延长线于M，证明△AME是等腰直角三角形，得出AM=EM=AE=AB，证出DG=AG=AD=AM=EM，得出GM=CD，证明△GEM≌△CGD（SAS），得出EG=CG，∠EGM=∠GCD，证出∠CGE=180°-90°=90°，即可得出EG⊥CG；
（2）延长EG至H，使HG=EG，连接DH、CH、CE，证明△EFG≌△HDG（SAS），得出EF=HD，∠EFG=∠HDG，证明△CBE≌△CDH（SAS），得出CE=CH，∠BCE=∠DCH，得出∠ECH=∠BCD=90°，证明△ECH是等腰直角三角形，得出CG=EH=EG，EG⊥CG；延长EG至H，使HG=EG，连接DH、CH、CE，同理可证CG=EH=EG，EG⊥CG；
（3）作EM垂直于CB的延长线与M，先求出BM，EM的值，即可根据勾股定理求出CE的长度，从而求出CG的长，即可求出面积.
【详解】
解：（1）EG=CG，EG⊥CG；理由如下：
过E作EM⊥AD交AD的延长线于M，如图1所示：
则∠M=90°，
∵四边形ABCD是正方形，
∴AB=AD=CD，∠BAD=∠D=90°，
∴∠BAM=90°，
∵△BEF是等腰直角三角形，
∴∠BAE=45°，AE=AB，
∴∠MAE=45°，
∴△AME是等腰直角三角形，
∴AM=EM=AE=AB，
∵G是DF的中点，
∴DG=AG=AD=AM=EM，
∴GM=CD，
在△GEM和△CGD中，
，
∴△GEM≌△CGD（SAS），
∴EG=CG，∠EGM=∠GCD，
∵∠GCD+∠DGC=90°，
∴∠EGM+∠DGC=90°，
∴∠CGE=180°-90°=90°，
∴EG⊥CG；
（2）当点F在AB上（不与点A重合）时，（1）中的结论仍然成立，理由如下：
延长EG至H，使HG=EG，连接DH、CH、CE，如图2所示：
∵G是DF的中点，
∴FG=DG，
在△EFG和△HDG中，，
∴△EFG≌△HDG（SAS），
∴EF=HD，∠EFG=∠HDG，
∵△BEF是等腰直角三角形，
∴EF=BE，∠BFE=∠FBE=45°，
∴BE=DH，
∵四边形ABCD是正方形，
∴AB∥CD，∠ABC=∠BCD=90°，BC=CD，
∴∠AFD=∠CDG，
∴∠AFE=∠CDH=135°，
∵∠CBE=90°+45°=135°，
∴∠CBE=∠CDH，
在△CBE和△CDH中，
，
∴△CBE≌△CDH（SAS），
∴CE=CH，∠BCE=∠DCH，
∴∠ECH=∠BCD=90°，
∴△ECH是等腰直角三角形，
∵EG=HG，
∴CG=EH=EG，EG⊥CG；
点F在AB的左侧时，（1）中的结论仍然成立，理由如下：
延长EG至H，使HG=EG，连接DH、CH、CE，如图3所示：
∵G是DF的中点，
∴FG=DG，
在△EFG和△HDG中，
，
∴△EFG≌△HDG（SAS），
∴EF=HD，∠EFG=∠HDG，
∵△BEF是等腰直角三角形，
∴EF=BE，∠BEF=90°，
∴BE=DH，
∵四边形ABCD是正方形，
∴AB∥CD，∠ABC=∠BCD=90°，BC=CD，
∴∠BNF=∠CDG，
∵∠EFG+∠BNF+∠BEF+∠ABE=∠HDG+∠CDG+∠CDH=360°，
∴∠BEF+∠ABE=∠CDH，
∴∠ABC+∠ABE=∠CDH，即∠CBE=∠CDH，
在△CBE和△CDH中，
，
∴△CBE≌△CDH（SAS），
∴CE=CH，∠BCE=∠DCH，
∴∠ECH=∠BCD=90°，
∴△ECH是等腰直角三角形，
∵EG=HG，
∴CG=EH=EG，EG⊥CG；
（3）如下图所示：作EM垂直于CB的延长线与M，
∵△BEF为等腰直角三角形，BF=3，
∴BE=，∠ABE=45°，
∵EM⊥BM，AB⊥CM，
∴∠EBM=45°，
∴△EMB为等腰直角三角形，
∴EM=BM=，
∵BC=4，
∴CM=，
∴CE=，
由（2）知，△GEC为等腰直角三角形，
∴CG=EG=，
∴S△CEG=.
本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质等腰直角三角形的判定与性质等知识；熟练掌握等腰直角三角形的判定与性质，证明三角形全等是解题的关键，属于压轴题型．
15、小路的宽为2米．
【解析】
根据“小路与观赏亭的面积之和占草坪面积的”，建立方程求解即可得出结论．
【详解】
设小路的宽为x米，
由题意得，（5x）2+（40+50）x﹣2×x×5x=×40×50
解得，x=2或x=﹣8（不合题意，舍去）
答：小路的宽为2米．
考查一元二次方程的应用，读懂题目，找出题目中的等量关系列出方程是解题的关键.
16、 (1) A坐标（4,0）、B 坐标（0 , 4）(2) D（4, 2）.
【解析】
分析：（1）令x=0求出与y轴的交点，令y=0求出与x轴的交点；
（2）由（1）可得△AOB为等腰直角三角形，则∠BAO=45°，因为点D和点C关于直线AB对称，所以∠BAO=∠BAD=45°，所以AD∥y轴且AD=AC，即可求得点D的坐标。
详解:（1） ∵直线y=-x+4分别与x轴、y轴交于A、B两点，
当x=0时，则y=4；当y=0，则x=4，
∴点A坐标为（4,0）、点B 坐标为（0, 4），
（2）D点坐标为D（4,2）.
点睛：本题考查了一次函数与坐标轴的交点，等腰直角三角形的判定与性质，轴对称的性质，熟练掌握一次函数与坐标轴的交点、轴对称的性质是解答本题的关键.
17、（1）修建的两块矩形绿地的面积共为144平方米，（2）人行通道的宽度为1米．
【解析】
根据题意得：两块矩形绿地的长为米，宽为米，可求得面积；
设人行通道的宽度为x米，则两块矩形绿地的长为米，宽为米，
根据题意得：，解方程可得.
【详解】
解：根据题意得：
两块矩形绿地的长为米，
宽为米，
面积为米，
答：修建的两块矩形绿地的面积共为144平方米，
设人行通道的宽度为x米，
则两块矩形绿地的长为米，
宽为米，
根据题意得：，
解得：舍去，，
答：人行通道的宽度为1米．
本题考核知识点：一元二次方程应用. 解题关键点：根据题意列出方程.
18、，．
【解析】
根据分式的减法和除法可以化简题目中的式子，然后将a的值代入化简后的式子即可解答本题．
【详解】
原式====．
当a=3时，原式==．
本题考查了分式的化简求值，解答本题的关键是明确分式化简求值的方法．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
由，即成比例的数的问题中，设出辅助参量表示另外两个量代入求值即可，
【详解】
解：因为，设 则
所以．
故答案为：
本题考查以成比例的数为条件求分式的值是常规题，掌握辅助参量法是解题关键．
20、﹣1＜b＜1
【解析】
当直线y=x+b过D或B时，求得b，即可得到结论．
【详解】
∵正方形ABCD的边长为1，点A的坐标为（1，1），∴D（1，3），B（3，1）．
当直线y=x+b经过点D时，3=1+b，此时b=1．
当直线y=x+b经过点B时，1=3+b，此时b=﹣1．
所以，直线y=x+b与正方形有两个公共点，则b的取值范围是﹣1＜b＜1．
故答案为﹣1＜b＜1．
本题考查了一次函数图象上点的坐标特征，正方形的性质，关键是掌握待定系数法正确求出函数的解析式．
21、75°
【解析】
连接BD,根据BD,AC为正方形的两条对角线可知AC为BD的垂直平分线,所以∠AMD=AMB,求∠AMD,∠AMB，再根据三角形内角和可得.
【详解】
如图，连接BD，
∵∠BCE=∠BCD+∠DCE=90°+60°=150°，BC=EC，
∴∠EBC=∠BEC=（180°-∠BCE）=15°,
∵∠BCM=∠BCD=45°，
∴∠BMC=180°-（∠BCM+∠EBC）=120°
∴∠AMB=180°-∠BMC=60°
∵AC是线段BD的垂直平分线，M在AC上，
∴∠AMD=∠AMB=60°，
∴∠ADM=180〬-∠DAC-∠AMD=180〬-45〬-60〬=75〬.
故答案为75〬
本题考核知识点：正方形性质，等边三角形. 解题关键点：运用正方形性质，等边三角形性质求角的度数.
22、
【解析】
首先求出AB的长，进而得出EO的长，再利用锐角三角函数关系求出E点横纵坐标即可.
解：如图所示，过E作EM⊥AC，
已知四边形ABCD是菱形，且周长为16，∠BAD=60°，根据菱形的性质可得AB=CD-BC=AD=4，AC⊥DB，∠BAO=∠BAD=30°，又因E是AB的中点，根据直角三角形中，斜边的中线等于斜边的一半可得EO=EA=EB=AB=2，根据等腰三角形的性质可得∠BAO=∠EOA=30°，由直角三角形中，30°的锐角所对的直角边等于斜边的一半可得EM=OE=1，在Rt△OME中，由勾股定理可得OM=，所以点E的坐标为（，1），
故选B.
“点睛”此题主要考查了菱形的性质以及锐角三角函数关系应用，根据已知得出EO的长以及∠EOA=∠EAO=30°是解题的关键.
23、
【解析】
试题解析：∵AD∥BC，
∴∠EDB=∠CBD，又∠EBD=∠CBD，
∴∠EBD=∠EDB，
∴EB=ED，又BC′=BC=AD，
∴EA=EC′，
在Rt△EC′D中，
DE2=EC′2+DC′2，即DE2=（8-DE）2+62，
解得DE=．
二、解答题（本大题共3个小题，共30分）
24、（1）当x≥3时，y与x之间的函数关系式是y=x+；（2）乘车13km应付车费21元；（3）出租车行驶了28千米．
【解析】
试题分析：（1）由于x≥3时，直线过点（3，8）、（8，15），设解析式为设y=kx+b，利用待定系数法即可确定解析式；
（2）把x=13代入解析式即可求得；
（3）将y=42代入到（1）中所求的解析式，即可求出x．
解：（1）当x≥3时，设解析式为设y=kx+b，
∵一次函数的图象过B（3，7）、C（8，14），
∴，
解得，
∴当x≥3时，y与x之间的函数关系式是y=x+；
（2）当x=13时，y=×13+=21，
答：乘车13km应付车费21元；
（3）将y=42代入y=x+，得42=x+，
解得x=28，
即出租车行驶了28千米．
25、当运动时间为秒或秒时，以点，，，为顶点的四边形是平行四边形．
【解析】
分别从当Q运动到E和B之间、当Q运动到E和C之间去分析求解即可求得答案．
【详解】
解：是的中点，
，
①当运动到和之间，设运动时间为，则得：
，
解得：；
②当运动到和之间，设运动时间为，则得：
，
解得：，
当运动时间为秒或秒时，以点，，，为顶点的四边形是平行四边形．
此题考查了梯形的性质以及平行四边形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想、分类讨论思想与方程思想的应用．
26、（1）见解析如图（1）；（2）三边分别为，3,2是格点三角形.图见解析.
【解析】
（1）根据勾股定理画出图形即可．
（2）先将等式变形，根据算术平方根和平方的非负性可得m和n的值，计算d的值，画出格点三角形即可．
【详解】
（1）如图（1）所示：
（2）∵，
∴，
解得：m=3,n=2,
∴三边长为3,2，或，3,2，
如图（2）所示：，3,2是格点三角形.
本题考查的是勾股定理，格点三角形、算术平方根和平方的非负性，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
题号
一
二
三
四
五
总分
得分