山东省济宁邹城县联考2025届数学九上开学达标测试试题【含答案】

这是一份山东省济宁邹城县联考2025届数学九上开学达标测试试题【含答案】，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图所示，在矩形中，，，矩形内部有一动点满足，则点到，两点的距离之和的最小值为（ ）.
A．B．C．D．
2、（4分）下列计算中，正确的是（ ）
A．+=B．×=3
C．÷=3D．=﹣3
3、（4分）已知平行四边形中，，如果添加一个条件，使得该四边形成为正方形，那么所添加的这个条件可以是（ ）
A．B．C．D．
4、（4分）如图，在四边形中，，点分别为线段上的动点(含端点，但点不与点重合)，点分别为的中点，则长度的最大值为( )
A．B．C．D．
5、（4分）下列多项式能用完全平方公式分解因式的有( )
A．B．C．D．
6、（4分）平行四边形两个内角的度数的比是1:2，则其中较小的内角是（ ）
A．B．C．D．
7、（4分）▱ABCD中，∠A＝50°，两条对角线相交于点O，下列结论正确的是（ ）
A．∠ABC＝50°B．∠BCD＝50°C．AB＝BCD．OB＝OC
8、（4分）四边形ABCD的对角线互相平分，要使它变为矩形，需要添加的条件是（ ）
A．AB=CDB．AB=BCC．AC⊥BDD．AC=BD
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）关于x的分式方程有增根，则a＝_____．
10、（4分）八年级（1）班四个绿化小组植树的棵数如下：8，8，10， x ．已知这组数据的众数和 平均数相等，那么这组数据的方差是_____．
11、（4分）函数y=中，自变量x的取值范围是___________．
12、（4分） 分解因式：9a﹣a3＝_____．
13、（4分）如图，在长20米、宽10米的长方形草地内修建了宽2米的道路，则草地的面积是______平方米．
三、解答题（本大题共5个小题，共48分）
14、（12分）在⊿ABC中，AB=17cm，BC=16cm，，BC边上的中线AD=15cm，问⊿ABC是什么形状的三角形？并说明你的理由.
15、（8分）某商店分两次购进 A．B两种商品进行销售，两次购进同一种商品的进价相同，具体情况如下表所示：
（1）求A、B两种商品每件的进价分别是多少元？
（2）商场决定A种商品以每件30元出售，B种商品以每件100元出售．为满足市场需求，需购进A、B两种商品共1000件，且A种商品的数量不少于B种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．
16、（8分）做服装生意的王老板经营甲、乙两个店铺，每个店铺在同一段时间内都能售出A，B两种款式的服装合计30件，并且每售出一件A款式和B款式服装，甲店铺获毛利润分别为30元和40元，乙店铺获毛利润分别为27元和36元．某日王老板进货A款式服装35件，B款式服装25件．怎样分配给每个店铺各30件服装，使得在保证乙店铺毛利润不小于950元的前提下，王老板获取的总毛利润最大？最大的总毛利润是多少？
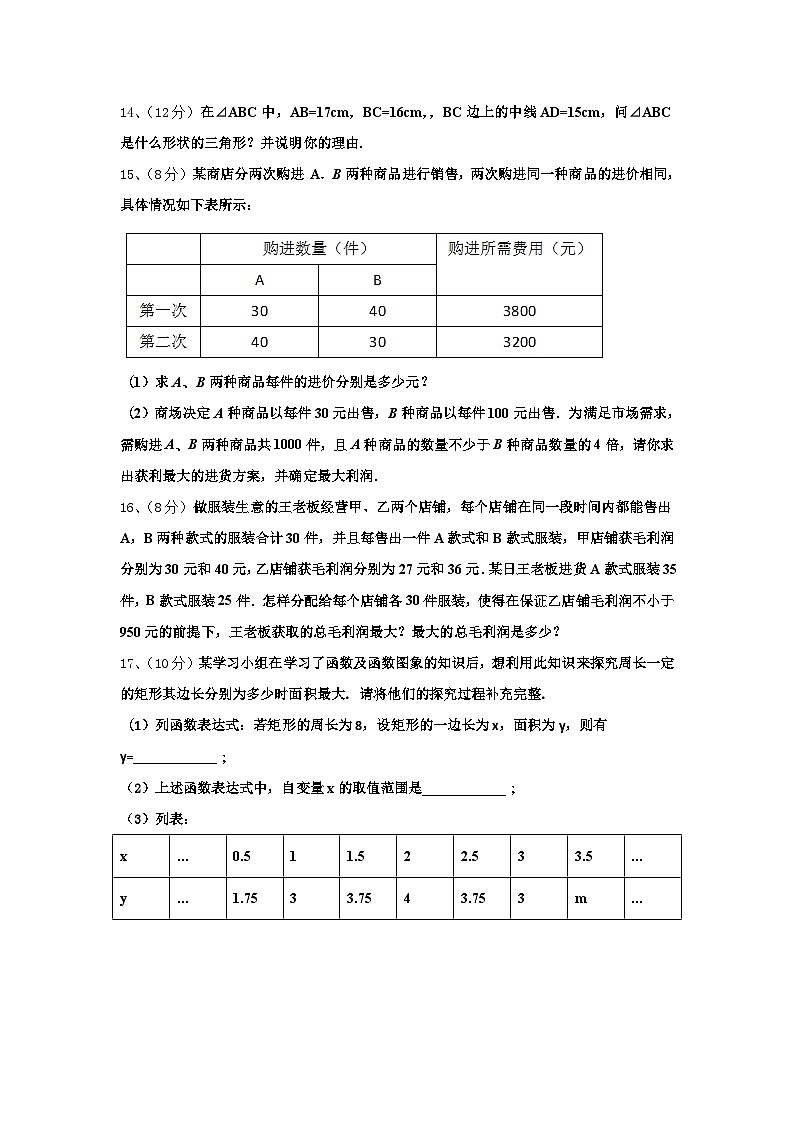
17、（10分）某学习小组在学习了函数及函数图象的知识后，想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.
（1）列函数表达式：若矩形的周长为8，设矩形的一边长为x，面积为y，则有y=____________；
（2）上述函数表达式中，自变量x的取值范围是____________；
（3）列表：

写出m=____________；
（4）画图：在平面直角坐标系中已描出了上表中部分各对应值为坐标的点，请你画出该函数的图象；
（5）结合图象可得，x=____________时，矩形的面积最大；写出该函数的其它性质（一条即可）：____________.
18、（10分）如图，在直角坐标系中，A（﹣1，2），B（﹣4，﹣2）．
（1）分别作点A，B关于原点的对称点C，D，并写出点C，点D的坐标；
（2）依次连接AB，BC，CD，DA，并证明四边形ABCD是平行四边形．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图,菱形ABCD的周长为12,∠B=60°,则菱形的面积为_________m2
20、（4分）比较大小：________.
21、（4分）当_____________时，在实数范围内有意义．
22、（4分）如果一梯子底端离建筑物9 m远，那么15 m长的梯子可到达建筑物的高度是____m．
23、（4分）将直线的图象向上平移3个单位长度，得到直线______．
二、解答题（本大题共3个小题，共30分）
24、（8分）近年来，萧山区大力发展旅游业，跨湖桥遗址、湘湖二期三期、宋城千古情、河上民俗、大美进化……这些名词，相信同学们都耳熟能详了，因此近年来，我区的年游客接待量呈逐年稳步上升，2015年接待1800万人次，2015——2017年这三年累计接待游客高达5958万人次.
(1)求萧山区2015——2017年年游客接待量的年平均增长率.
(2)若继续呈该趋势增长，请预测2018年年游客接待量（近似到万人次）.
25、（10分）如图，平行四边形的顶点分别在轴和轴上，顶点在反比例函数的图象上，求平行四边形的面积．
26、（12分）解下列一元二次方程
(1) (2)
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
首先由，得出动点P在与AB平行且与AB的距离是2的直线l上，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离．然后在直角三角形ABE中，由勾股定理求得BE的值，即PA＋PB的最小值．
【详解】
解：设△ABP中AB边上的高是h．
∵，
∴AB•h＝AB•AD，
∴h＝AD＝2，
∴动点P在与AB平行且与AB的距离是2的直线l上，如图，作A关于直线l的对称点E，连接AE，BE，则BE的长就是所求的最短距离．
在Rt△ABE中，∵AB＝4，AE＝2＋2＝4，
∴BE＝，
即PA＋PB的最小值为．
故选D．
本题考查了轴对称−最短路线问题，三角形的面积，矩形的性质，勾股定理，两点之间线段最短的性质．得出动点P所在的位置是解题的关键．
2、C
【解析】
根据二次根式的性质和乘除法运算法则，对每个选项进行判断，即可得到答案.
【详解】
解：A、与不是同类二次根式，不能合并，故A错误；
B、，故B错误；
C、，故C正确；
D、，故D错误；
故选择：C.
本题考查了二次根式的性质，二次根式的乘除运算，以及同类二次根式的定义，解题的关键是熟练掌握二次根式的性质，以及熟记乘除法运算的运算法则.
3、C
【解析】
由已知可得该四边形为矩形，再添加条件：一组邻边相等，即可判定为正方形．
【详解】
由∠A=∠B=∠C=90°可判定四边形ABCD为矩形，因此再添加条件：一组邻边相等，即可判定四边形ABCD为正方形，
故选：C．
本题考查正方形的判定．正方形的判定方法有：①先判定四边形是矩形，再判定这个矩形有一组邻边相等；②先判定四边形是菱形，再判定这个菱形有一个角为直角；③先判定四边形是平行四边形，再用1或2进行判定．
4、B
【解析】
连接BD、ND，由勾股定理得可得BD=5，由三角形中位线定理可得EF=DN，当DN最长时，EF长度的最大，即当点N与点B重合时，DN最长，由此即可求得答案.
【详解】
连接BD、ND，
由勾股定理得，BD==5
∵点E、F分别为DM、MN的中点，
∴EF=DN，
当DN最长时，EF长度的最大，
∴当点N与点B重合时，DN最长，
∴EF长度的最大值为BD=2.5，
故选B．
本题考查了勾股定理，三角形中位线定理，正确分析、熟练掌握和灵活运用相关知识是解题的关键.
5、C
【解析】
根据完全平方公式的形式即可判断.
【详解】
∵=(x-2)2
故选C.
此题主要考查公式法因式分解，解题的关键是熟知完全平方公式的形式特点.
6、C
【解析】
根据平行四边形的性质可知，平行四边形的对角相等，邻角互补，故该平行四边形的四个角的比值为1：2：1：2，所以可以计算出平行四边形的各个角的度数．
【详解】
根据平行四边形的相邻的两个内角互补知，设较小的内角的度数为x，
则有：x+2x=180°
∴x=60°，
即较小的内角是60°
故选C.
此题考查平行四边形的性质，解题关键在于设较小的内角的度数为x
7、B
【解析】
根据平行四边形的性质逐项分析即可．
【详解】
如图：
∵四边形ABCD是平行四边形，
∴∠A+∠ABC＝180°，∠DAB＝∠BCD＝50°，AB＝DC，OB＝OD，
∴∠ABC＝130°，
由上可知正确的结论为B，
故选：B．
此题考查了平行四边形的性质．此题难度不大，注意熟记平行四边形的性质定理是关键．
8、D
【解析】
四边形ABCD的对角线互相平分，则说明四边形是平行四边形，由矩形的判定定理知，只需添加条件是对角线相等．
【详解】
添加AC=BD，
∵四边形ABCD的对角线互相平分，
∴四边形ABCD是平行四边形，
∵AC=BD，根据矩形判定定理对角线相等的平行四边形是矩形，
∴四边形ABCD是矩形，
故选D．
考查了矩形的判定，关键是掌握矩形的判定方法：①矩形的定义：有一个角是直角的平行四边形是矩形；②有三个角是直角的四边形是矩形；③对角线相等的平行四边形是矩形．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、a=-1
【解析】
根据分式方程的解法求出方程的解，然后根据方程有增根，则x=－5，从而得出a的值．
【详解】
去分母可得：1+a=x+5， 解得：x=a－2， ∵分式方程有增根， ∴x=－5，即a－2=－5，
解得：a=－1．
本题主要考查的是分式方程的解得情况，属于中等难度的题型．分式方程有增根是因为整式方程的解会使得分式的分母为零．
10、1.
【解析】
根据题意先确定x的值，再根据方差公式进行计算即可.
【详解】
解：当x=10时，有两个众数，而平均数只有一个，不合题意舍去．
当众数为8时，根据题意得，
解得x=6，
则这组数据的方差是：.
故答案为1．
本题考查了数据的收集和处理，主要考查了众数、平均数和方差的知识，解题时需要理解题意，分类讨论．
11、且x≠−1.
【解析】
根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，列不等式求解．
【详解】
根据题意，可得
且x+1≠0；
解得且x≠−1.
故答案为且x≠−1.
考查函数自变量的取值范围，熟练掌握分式有意义的条件，二次根式有意义的条件是解题的关键.
12、a（3+a）（3﹣a）．
【解析】
先提公因式，再用平方差公式，可得答案．
【详解】
原式=a（9﹣a2）=a（3+a）（3﹣a）．
故答案为：a（3+a）（3﹣a）．
本题考查了因式分解，利用提公因式与平方差公式是解题的关键．
13、144米1．
【解析】
将道路分别向左、向上平移，得到草地为一个长方形，分别求出长方形的长和宽，再用长和宽相乘即可．
【详解】
解：将道路分别向左、向上平移，得到草地为一个长方形，
长方形的长为10-1=18（米），宽为10-1=8（米），
则草地面积为18×8=144米1．
故答案为：144米1．
本题考查了平移在生活中的运用，将道路分别向左、向上平移，得到草地为一个长方形是解题的关键．
三、解答题（本大题共5个小题，共48分）
14、等腰直角三角形，理由见解析.
【解析】
试题分析: 先根据AD是BD上的中线求出BD的长，再根据勾股定理的逆定理判断出△ABD的形状，进而可得出∠ADC=90°，根据勾股定理即可求出AC的长，进而得出结论．
试题解析:
△ABC是等腰三角形，
∵AD是BC边的中线，BC=16cm，
∴BD=DC=8cm，
∵AD ²+BD ²=15 ²+8 ²=17 ²=AB ²，
∴∠ADB=90°，
∴∠ADC=90°，
在Rt△ADC中，
AC==17cm.
∴AC=AB，
即△ABC是等腰三角形.
点睛: 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
15、（1）A种商品每件的进价为20元，B种商品每件的进价为80元；（2）当购进A种商品800件、B种商品2件时，销售利润最大，最大利润为120元．
【解析】
试题分析：（1）设A种商品每件的进价为x元，B种商品每件的进价为y元，根据两次进货情况表，可得出关于x、y的二元一次方程组，解之即可得出结论；
（2）设购进B种商品m件，获得的利润为w元，则购进A种商品（1000﹣m）件，根据总利润=单件利润×购进数量，即可得出w与m之间的函数关系式，由A种商品的数量不少于B种商品数量的4倍，即可得出关于m的一元一次不等式，解之即可得出m的取值范围，再根据一次函数的性质即可解决最值问题．
试题解析：（1）设A种商品每件的进价为x元，B种商品每件的进价为y元，
根据题意得：，解得：．
答：A种商品每件的进价为20元，B种商品每件的进价为80元．
（2）设购进B种商品m件，获得的利润为w元，则购进A种商品（1000﹣m）件，
根据题意得：w=（30﹣20）（1000﹣m）+（100﹣80）m=10m+1．
∵A种商品的数量不少于B种商品数量的4倍，
∴1000﹣m≥4m，
解得：m≤2．
∵在w=10m+1中，k=10＞0，
∴w的值随m的增大而增大，
∴当m=2时，w取最大值，最大值为10×2+1=120，
∴当购进A种商品800件、B种商品2件时，销售利润最大，最大利润为120元．
考点：一次函数的应用，二元一次方程组的应用，解一元一次不等式.
16、分配给甲店铺A、B两种款式服装分别为21件和9件，分配给乙店铺A，B两种款式服装分别为14件和16件，最大的总毛利润为1944元.
【解析】
设A款式服装分配到甲店铺为x件，则分配到乙店铺为（35-x）件；B款式分配到甲店铺为（30-x）件，分配到乙店铺为（x-5）件，总利润为y元，依题意可得到一个函数式和一个不等式，可求解．
【详解】
设分配给甲店铺A款式服装x件（x取整数，且5≤x≤30），则分配给甲店铺B款装（30-x）件，分配给乙店铺A款服装（35-x）件，分配给乙店铺B款式服装[25-(30-x)]=(x-5)件，总毛利润（设为y总）为：
Y总=30x+40(30-x)+27(35-x)+36(x-5)=-x+1965
乙店铺的毛利润（设为y乙）应满足：
Y乙=27(35-x)+36(x-5)≥950，得x≥
对于y总=-x+1965,y随着x的增大而减小，要使y总最大，x必须取最小值，又x≥,
故取x=21，即分配给甲店铺A、B两种款式服装分别为21件和9件，分配给乙店铺A，B两种款式服装分别为14件和16件，此时既保证了乙店铺获毛利润不小于950元，又保证了在此前提下王老板获取的总毛利润最大，
最大的总毛利润为y总最大=－21+1965=1944（元）
考点：一次函数的应用．
17、见解析
【解析】
（1）根据矩形的周长表示出另一边长，然后利用矩形面积公式即可求得y与x间的关系式；
（2）根据矩形周长以及边长大于0即可求得；
（3）把x=3.5代入（1）中的解析式即可求得m的值；
（4）按从左到右的顺序用平滑的曲线进行画图即可；
（5）观察图象即可得.
【详解】
（1）因为矩形一边长为x，则另一边长为（-x）=（4-x），
依题意得：矩形的面积y=x（4-x），
即y=-x2+4x，
故答案为：-x2 + 4x；
（2）由题意得，解得：0＜x＜4，
故答案为：0＜x＜4；
（3）当x=3.5时，y=-3.52+4×3.5=1.75，
故答案为：1.75；
（4）如图所示；
（5）观察图象可知当x=2时矩形面积最大，
轴对称图形；当0＜x≤2时，y随x的增大而增大等，
故答案为：2；轴对称图形或当0＜x≤2时，y随x的增大而增大.
本题考查了二次函数的应用，正确理解题意，得出函数解析式是解题的关键.注意数形结合思想的运用.
18、（1）点C，点D的坐标分别为：（1，﹣2），（4，2）；（2）见解析.
【解析】
（1）直接利用关于原点对称点的性质进而得出答案；
（2）利用平行四边形的判定方法得出答案．
【详解】
（1）解：∵A（﹣1，2），B（﹣4，﹣2），点A，B关于原点的对称点C，D，
∴点C，点D的坐标分别为：（1，﹣2），（4，2）；
（2）证明：
∵AD＝BC＝4+1＝5，
∵A（﹣1，2），B（﹣4，﹣2），C（1，﹣2），D（4，2）；
∴AD∥BC，
∴四边形ABCD是平行四边形．
此题主要考查了旋转变换以及平行四边形的判定，正确把握平行四边形的判定方法是解题关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
首先根据已知求得菱形的边长，再根据勾股定理求得其两条对角线的长，进而求出菱形的面积．
【详解】
解：菱形的周长为12，
菱形的边长为3，
四边形是菱形，且，
为等边三角形，，
，
，
菱形的面积，
故答案为
本题主要考查了菱形的性质，解题的关键是熟练掌握菱形的面积等于对角线乘积的一般，此题难度不大．
20、＜
【解析】
试题解析：∵
∴
∴
21、a≥1
【解析】
根据二次根式有意义的条件可得a-1≥0，再解不等式即可．
【详解】
由题意得：a-1≥0，
解得：a≥1，
故答案为： a≥1．
此题主要考查了二次根式有意义的条件，关键是掌握二次根式中的被开方数是非负数．
22、12
【解析】
∵直角三角形的斜边长为15m，一直角边长为9m，
∴另一直角边长=，
故梯子可到达建筑物的高度是12m．
故答案是：12m.
23、
【解析】
上下平移时只需让的值加减即可.
【详解】
原直线的，，向上平移3个单位长度得到了新直线，那么新直线的，，所以新直线的解析式为：.
故答案为：.
考查了一次函数图象与几何变换，要注意求直线平移后的解析式时的值不变，只有发生变化.
二、解答题（本大题共3个小题，共30分）
24、（1）年平均增长率为10% ；（2）.
【解析】
设萧山区从2015——2017年年游客接待量的年平均增长率为x，根据这三年累计接待游客高达5958万人次即可得出关于x的一元二次方程，解出取其正值即可得出结论；
（2）运用（1）的结论进行预测即可.
【详解】
（1）解：设年平均增长率为x得：
由题意得：x＞0，∴（舍去）即年平均增长率为10%
（2）
∴若继续呈该趋势增长，预测2018年年游客接待量约为2396万人次.
本题考查了一元二次方程的应用，解题珠关键是找准等量关系，正确列出一元二次方程.
25、3
【解析】
根据题意可知B点的横坐标和纵坐标分别是平行四边形的底和高，根据平行四边形的面积公式及反比例函数系数的几何意义，即可得出.
【详解】
∵平行四边形ABOC定点A、C分别在y轴和x轴上，顶点B在反比例函数y= 的图象上，设B点横坐标为a，则纵坐标为 ，
∴S平行四边形AB0C=AB∙OA=a∙=3，
故本题答案为：3.
本题考查了反比例函数系数k的几何意义以及平行四边形的面积公式，根据反比例函数系数k的几何意义找出S平行四边形 ABOC=|k|.
26、；.
【解析】
(1)利用因式分解法进行求解即可；
(2)利用公式法进行求解即可.
【详解】
(1)，
(x+2)(x+8)=0
x+2=0或x+8=0，
所以；
(2)，
a=3，b=6，c=-2，
b2-4ac=62-4×3×(-2)=60>0，
x===-1±，
所以.
本题考查了解一元二次方程，根据一元二次方程的特点选择适当的方法进行求解是解题的关键.
题号
一
二
三
四
五
总分
得分
批阅人
x
…
0.5
1
1.5
2
2.5
3
3.5
…
y
…
1.75
3
3.75
4
3.75
3
m
…