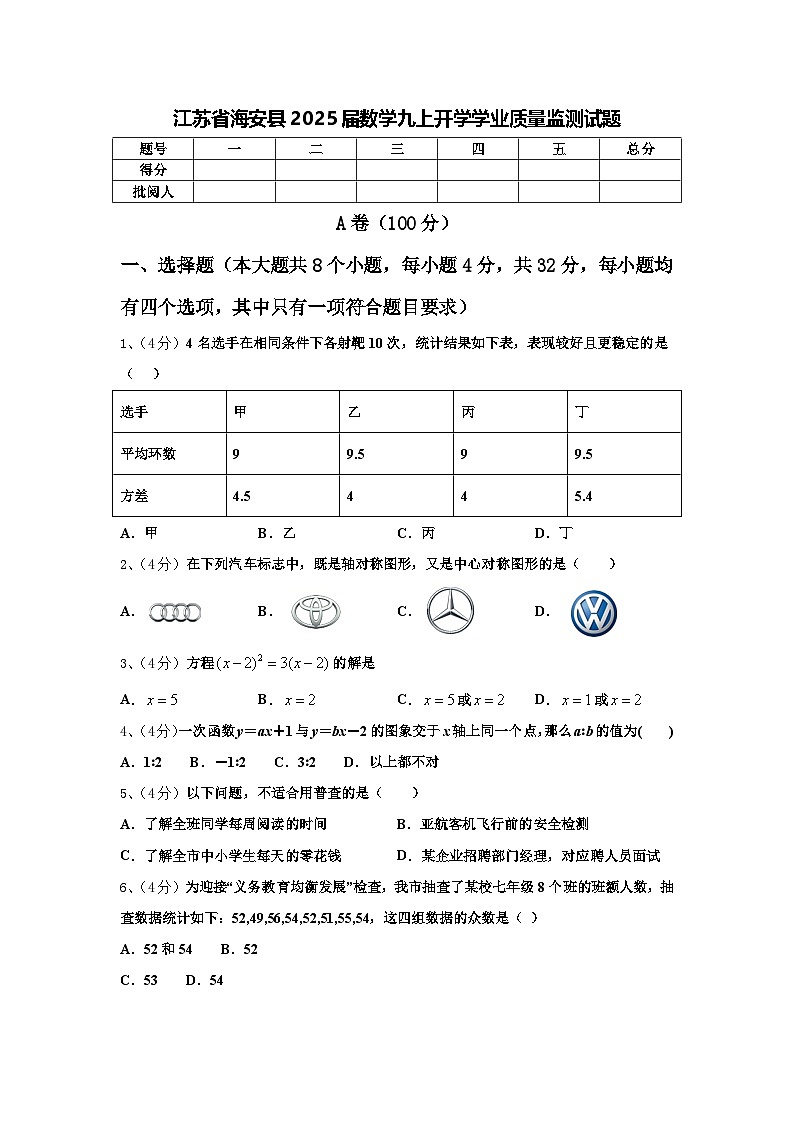
江苏省海安县2025届数学九上开学学业质量监测试题【含答案】

这是一份江苏省海安县2025届数学九上开学学业质量监测试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）4名选手在相同条件下各射靶10次，统计结果如下表，表现较好且更稳定的是（ ）
A．甲B．乙C．丙D．丁
2、（4分）在下列汽车标志中，既是轴对称图形，又是中心对称图形的是（ ）
A．B．C．D．
3、（4分）方程的解是
A．B．C．或D．或
4、（4分）一次函数y＝ax＋1与y＝bx－2的图象交于x轴上同一个点，那么a∶b的值为( )
A．1∶2 B．－1∶2 C．3∶2 D．以上都不对
5、（4分）以下问题，不适合用普查的是（ ）
A．了解全班同学每周阅读的时间B．亚航客机飞行前的安全检测
C．了解全市中小学生每天的零花钱D．某企业招聘部门经理，对应聘人员面试
6、（4分）为迎接“义务教育均衡发展”检查，我市抽查了某校七年级8个班的班额人数，抽查数据统计如下：52,49,56,54,52,51,55,54，这四组数据的众数是（ ）
A．52和54 B．52
C．53 D．54
7、（4分）已知关于的方程是一元二次方程，则的取值范围是（ ）
A．B．C．D．任意实数
8、（4分）如图，在中，，是的平分线，于点，平分，则等于（ ）
A．1．5°B．30°C．25°D．40°
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，在平面直角坐标系xy中，矩形ABCD的边AB在x轴上，AO=2，BO=3，BC=4.将正方形沿箭头方向推，使点D落在y轴正半轴上点D’处，则点C的对应点C’的坐标为____.
10、（4分）数据-2，-1，0，1，2，4的中位数是________ 。
11、（4分）若一组数据的平均数为17，方差为2，则另一组数据的平均数和方差分别为（ ）
A．17，2B．18，2C．17，3D．18，3
12、（4分）在一个长为2米，宽为1米的矩形草地上，如图堆放着一根长方体的木块，它的棱长和场地宽AD平行且＞AD，木块的正视图是边长为0.2米的正方形，一只蚂蚁从点A处，到达C处需要走的最短路程是________米．
13、（4分）如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是_____________．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在中，点，是直线上的两点，，连结，，，．
（1）求证：四边形是平行四边形．
（2）若，，，四边形是矩形，求的长．
15、（8分）丽君花卉基地出售两种盆栽花卉：太阳花6元/盆，绣球花10元/盆．若次购买的绣球花超过20盆时，超过20盆部分的绣球花价格打8折．
（1）求出太阳花的付款金额（元）关于购买量（盆）的函数关系式；
（2）求出绣球花的付款金额（元）关于购买量（盆）的函数关系式；
（3）为了美化环境，花园小区计划到该基地购买这两种花卉共90盆，其中太阳花数量不超过绣球花数量的一半．两种花卉各买多少盆时，总费用最少，最少费用是多少元？
16、（8分）如图，在△ABC中，∠ACB＝90°，∠CAB＝30°， AC＝4.5cm． M是边AC上的一个动点，连接MB，过点M作MB的垂线交AB于点N． 设AM=x cm，AN=y cm．（当点M与点A或点C重合时，y的值为0）
探究函数y随自变量x的变化而变化的规律．
（1） 通过取点、画图、测量，得到了x与y的几组对应值，如下表：
（要求：补全表格，相关数值保留一位小数）
（2）建立平面直角坐标系xOy，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：当AN=AM时，AM的长度约为 cm（结果保留一位小数）．
17、（10分）某商场计划购进甲、乙两种商品共件，这两种商品的进价、售价如表所示：
设购进甲种商品（，且为整数）件，售完此两种商品总利润为元．
（1）该商场计划最多投入元用于购进这两种商品共件，求至少购进甲种商品多少件？
（2）求与的函数关系式；
（3）若售完这些商品，商场可获得的最大利润是__________元．
18、（10分）已知y与x+3成正比例，且当x=1时，y=8
（1）求y与x之间的函数关系式；
（2）若点（a，6）在这个函数的图象上，求a的值.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）已知，如图，△ABC中，E为AB的中点，DC∥AB，且DC＝AB，请对△ABC添加一个条件：_____，使得四边形BCDE成为菱形．
20、（4分）若分式在实数范围内有意义，则x的取值范围是_____．
21、（4分）直线y=3x-2不经过第________________象限．
22、（4分）如图，两张等宽的纸条交叉叠放在一起，若重合部分构成的四边形中，，，则的长为_______________．
23、（4分）若关于的一元二次方程有两个相等的实数根，则的值是__________．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图,已知.利用直尺和圆规,根据下列要求作图(不写作法,保留作图痕迹),并回答问题:
(1)作的平分线、交于点；
(2)作线段的垂直平分线,交于点，交于点,连接；
(3)写出你所作出的图形中的所有等腰三角形.
25、（10分）为了了解某公司员工的年收入情况，随机抽查了公司部分员工年收入情况并绘制如图所示统计图.
（1）请按图中数据补全条形图；
（2）由图可知员工年收入的中位数是 ，众数是 ；
（3）估计该公司员工人均年收入约为多少元？
26、（12分）某校为灾区开展了“献出我们的爱”赈灾捐款活动，九年级（1）班50名同学积极参加了这次赈灾捐款活动，因不慎，表中数据有一处被墨水污染，已无法看清，但已知全班平均每人捐款38元.
（1）根据以上信息可知，被污染处的数据为 .
（2）该班捐款金额的众数为 ，中位数为 .
（3）如果用九年级（1）班捐款情况作为一个样本，请估计全校2000人中捐款在40元以上（包括40元）的人数是多少？
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
先比较平均数，乙、丁的平均成绩好且相等，再比较方差即可解答．
【详解】
解：∵乙、丁的平均成绩大于甲、丙，且乙的方差小于丁的方差，
∴表现较好且更稳定的是乙，
故选：B．
本题考查方差的意义：反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
2、A
【解析】
根据中心对称图形和轴对称图形的概念逐一进行分析即可.
【详解】
A、是中心对称图形，也是轴对称图形，故符合题意；
B、不是中心对称图形，是轴对称图形，故不符合题意；
C、不是中心对称图形，是轴对称图形，故不符合题意；
D、不是中心对称图形，是轴对称图形，故不符合题意，
故选A.
本题主要考查轴对称图形和中心对称图形，在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形；在平面内，如果把一个图形绕某个点旋转180°后，能与原图形重合，那么就说这个图形是中心对称图形.
3、C
【解析】
方程移项后，利用因式分解法求出解即可．
【详解】
解：（x-2）2=3（x-2），
（x-2）2-3（x-2）=0，
（x-2）（x-2-3）=0，
x-2=0，x-2-3=0，
x1=2，x2=1．
故选C．
本题考查解一元二次方程-因式分解法，熟练掌握因式分解的方法是解题的关键．
4、B
【解析】
试题分析：先根据x轴上的点的横坐标相等表示出x的值，再根据相交于同一个点，则x值相等，列式整理即可得解．
解：∵两个函数图象相交于x轴上同一个点，
∴y=ax+1=bx﹣1=0，
解得x=﹣=，
所以=﹣，
即a：b=（﹣1）：1．
故选B．
5、C
【解析】
根据普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似判断即可．
【详解】
A、了解全班同学每周阅读的时间适合普查，故A不符合题意；
B、亚航客机飞行前的安全检测是重要的调查，故B不符合题意；
C、了解全市中小学生每天的零花钱适合抽要调查，故C符合题意；
D、某企业招聘部门经理，对应聘人员面试，适合普查，故D不符合题意；
故选C．
本题考查的是抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
6、A
【解析】
试题分析：众数是指一组数据中出现次数最多的数字，数据52和54都出现2次，其它只出现一次，所以，众数为52和54。
考点：众数的计算
7、A
【解析】
利用一元二次方程的定义求解即可．
【详解】
解：∵关于x的方程是一元二次方程，
∴m＋1≠0，即m≠−1，
故选：A．
此题主要考查了一元二次方程的概念．只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程，一般形式是ax2＋bx＋c＝0（且a≠0）．特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．
8、B
【解析】
利用全等直角三角形的判定定理HL证得Rt△ACD≌Rt△AED，则对应角∠ADC=∠ADE；然后根据已知条件“DE平分∠ADB”、平角的定义证得∠ADC=∠ADE=∠EDB=60°；最后由直角三角形的两个锐角互余的性质求得∠B=30°．
【详解】
∵在△ABC中，∠C=90°，AD是角平分线，DE⊥AB于E，
∴CD=ED．
在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴∠ADC=∠ADE（全等三角形的对应角相等）．
∵∠ADC+∠ADE+∠EDB=180°，DE平分∠ADB，
∴∠ADC=∠ADE=∠EDB=60°．
∴∠B+∠EDB=90°，
∴∠B=30°．
故选：B．
此题考查角平分线的性质．解题关键在于掌握角平分线的性质：角的平分线上的点到角的两边的距离相等．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、 (5,)
【解析】
由题知从正方形变换到平行四边形时，边的长度没变，从而求出即可
【详解】
由题知从正方形变换到平行四边形时，A D’=AD=BC=4，D’C’=AB=5，
∵AO=2，根据勾股定理，则O D’=，则D’（ 0,），故C’的坐标为(5,)
熟练掌握图形变化中的不变边和勾股定理计算是解决本题的关键
10、
【解析】
根据中位数的定义即可得．
【详解】
中位数为（0+1）÷2=.
故答案是：.
考查中位数，掌握：将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数是解题的关键．
11、B
【解析】
根据平均数和方差的变化规律，即可得出答案．
【详解】
∵数据x1+1，x1+1，，xn+1的平均数为17，
∴x1+1，x1+1，，xn+1的平均数为18，
∵数据x1+1，x1+1，，xn+1的方差为1，
∴数据x1+1，x1+1，，xn+1的方差不变，还是1；
故选B．
本题考查了方差与平均数，用到的知识点：如果一组数据x1，x1，，xn的平均数为，方差为S1，那么另一组数据ax1+b，ax1+b，，axn+b的平均数为a+b，方差为a1S1．
12、2.10
【解析】
由题意可知，将木块展开，
相当于是AB+2个正方形的宽，
∴长为2+0.2×2=2.4米；宽为1米．
于是最短路径为：
故答案是：2.1．
13、或或1
【解析】
如图所示：
①当AP=AE=1时，∵∠BAD=90°，∴△AEP是等腰直角三角形，∴底边PE=AE=；
②当PE=AE=1时，∵BE=AB﹣AE=8﹣1=3，∠B=90°，∴PB==4，∴底边AP===；
③当PA=PE时，底边AE=1；
综上所述：等腰三角形AEP的对边长为或或1；
故答案为或或1．
三、解答题（本大题共5个小题，共48分）
14、 (1)见解析；（2）
【解析】
（1）连结交于点,由四边形ABCD是平行四边形,可得OA=OC,OD=OB,又因为，从而OE=OF,可证四边形是平行四边形；
（2）由勾股定理可求出BD的长，进而求出OD的长，再由勾股定理求出AO的长，根据矩形的性质可知AO=EO，从而可求出DE的长.
【详解】
（1）连结交于点,
∵四边形ABCD是平行四边形,
∴OA=OC,OD=OB,
∵，
∴OE=OF,
四边形是平行四边形;
（2），，，
，
，
.
四边形是矩形，
，，，
，
.
本题考查了平行四边形的判定与性质，矩形的性质，勾股定理等知识，熟练掌握平行四边形的判定与性质是解答（1）的关键，熟练掌握矩形的性质是解（2）的关键.
15、（1）：y1=6x；（2）y2=；（3）太阳花30盆，绣球花60盆时，总费用最少，最少费用是700元
【解析】
（1）根据总价=单价×数量，求出太阳花的付款金额y1（元）关于购买量x（盆）的函数解析式；
（2分两种情况：①一次购买的绣球花不超过20盆；②一次购买的绣球花超过20盆；根据总价=单价×数量，求出绣球花的付款金额y2（元）关于购买量x（盆）的函数解析式即可；
（3）首先太阳花数量不超过绣球花数量的一半，可得太阳花数量不超过两种花数量的，即太阳花数量不超过30盆，所以绣球花的数量不少于60盆；然后设太阳花的数量是x盆，则绣球花的数量是90-x盆，根据总价=单价×数量，求出购买两种花的总费用是多少，进而判断出两种花卉各买多少盆时，总费用最少，最少费用是多少元即可．
【详解】
解：（1）太阳花的付款金额y1（元）关于购买量x（盆）的函数解析式是：y1=6x；
（2）①一次购买的绣球花不超过20盆时，
付款金额y2（元）关于购买量x（盆）的函数解析式是：y2=10x（x≤20）；
②一次购买的绣球花超过20盆时，
付款金额y2（元）关于购买量x（盆）的函数解析式是：
y2=10×20+10×0.8×(x-20)
=200+8x-160
=8x+40
综上，可得
绣球花的付款金额y2（元）关于购买量x（盆）的函数解析式是：
y2=
（3）根据题意，可得太阳花数量不超过：90×（盆），
所以绣球花的数量不少于：90-30=60（盆），
设太阳花的数量是x盆，则绣球花的数量是(90-x)盆，购买两种花的总费用是y元，
则x≤30，
则y=6x+[8(90-x)+40]
=6x+[760-8x]
=760-2x，
∵-2＜0，
∴y随x的增大而减小，
∵x≤30，
∴当x=30时，
y最小=760-2×30=700（元），
90-30=60盆，
答：太阳花30盆，绣球花60盆时，总费用最少，最少费用是700元．
本题主要考查了一次函数的应用，要熟练掌握，解答此题的关键是要明确：分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符合实际．此题还考查了单价、总价、数量的关系：总价=单价×数量，单价=总价÷数量，数量=总价÷单价，要熟练掌握．
16、（1）1.1； （2）详见解析；（3）3.1．
【解析】
（1）如图，作辅助线：过N作NP⊥AC于P，证明△NPM∽△MCB，列比例式可得结论；
（2）描点画图即可；
（3）同理证明△NPM∽△MCB，列比例式，解方程可得结论．
【详解】
解：（1）如图，过N作NP⊥AC于P，
Rt△ACB中，∠CAB＝30°， AC＝1.5cm．
∴BC=
当x=2时，即AM=2，
∴MC=2.5，
∵∠NMB=90°，
易得△NPM∽△MCB，
∴ = ，
设NP=5a，PM=9a，则AP=15a，AN=10a，
∵AM=2，
∴15a+9a=2，
a= ，
∴y=AN=10×1.73×≈1.1；
故答案为1.1；
（2）如图所示：
（3）设PN=a，则AN=2a，AP=a，
∵AN=AM，∴AM=1a,
如图，由（1）知：△NPM∽△MCB，
∴，即 ，
解得：a≈0.81，
∴AM=1a=1×0.81=3.36≈3.1（cm）．
故答案为（1）1.1； （2）详见解析；（3）3.1．
本题是三角形与函数图象的综合题，主要考查了含30度角的直角三角形的性质，相似三角形的判定和性质，函数图象的画法，直角三角形的性质，勾股定理，并与方程相结合，计算量比较大．
17、（1）50件；（2）；（3）795
【解析】
（1）根据表格中的数据和题意列不等式，根据且x为整数即可求出x的取值范围得到答案；
（2）根据题意和表格中的数据即可得到函数关系式；
（3）根据（2）中的函数关系式和一次函数的性质即可求出答案.
【详解】
（1）由题意得15x+25（80-x），
解得x，
∵，且为整数，
∴，且为整数，
∴至少购进甲种商品50件；
（2）由题意得，
∴y与x的函数关系式是；
（3）∵，，且为整数，
∴当x=1时，y有最大值，此时y最大值=795，
故答案为：795.
此题考查一元一次不等式的实际应用，一次函数的实际应用，一次函数的性质求函数的最大值，正确理解题意列不等式或函数解决问题是解题的关键.
18、（1）y=1x+6；（1）2.
【解析】
分析：（1）根据y与x+3成正比，设y=k（x+3），把x与y的值代入求出k的值，即可确定出关系式；
（1）把点（a，6）代入一次函数解析式求出a的值即可．
详解：（1）根据题意：设y=k（x+3），
把x=1，y=8代入得：8=k（1+3），
解得：k=1．
则y与x函数关系式为y=1（x+3）=1x+6；
（1）把点（a，6）代入y=1x+6得：6=1a+6，
解得a=2．
点睛：此题考查了待定系数法求一次函数解析式，熟练掌握待定系数法是解本题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、AB＝2BC．
【解析】
先由已知条件得出CD=BE，证出四边形BCDE是平行四边形，再证出BE=BC，根据邻边相等的平行四边形是菱形可得四边形BCDE是菱形．
【详解】
解：添加一个条件：AB＝2BC，可使得四边形BCDE成为菱形．理由如下：
∵DC＝AB，E为AB的中点，
∴CD＝BE＝AE．
又∵DC∥AB，
∴四边形BCDE是平行四边形，
∵AB＝2BC，
∴BE＝BC，
∴四边形BCDE是菱形．
故答案为：AB＝2BC．
本题考查了菱形的判定，平行四边形的判定；熟记平行四边形和菱形的判定方法是解决问题的关键．
20、x≠1
【解析】
分式有意义的条件是分母不等于零．
【详解】
∵分式在实数范围内有意义，
∴x−1≠0，
解得：x≠1.
故答案为：x≠1.
此题考查分式有意义的条件，解题关键在于分母不等于零使得分式有意义.
21、二
【解析】
根据已知求得k，b的符号，再判断直线y=3x-2经过的象限．
【详解】
解：∵k=3＞0，图象过一三象限，b=-2＜0过第四象限
∴这条直线一定不经过第二象限．
故答案为：二
此题考查一次函数的性质，一次函数y=kx+b的图象有四种情况：
①当k＞0，b＞0，函数y=kx+b的图象经过第一、二、三象限，y的值随x的值增大而增大；
②当k＞0，b＜0，函数y=kx+b的图象经过第一、三、四象限，y的值随x的值增大而增大；
③当k＜0，b＞0时，函数y=kx+b的图象经过第一、二、四象限，y的值随x的值增大而减小；
④当k＜0，b＜0时，函数y=kx+b的图象经过第二、三、四象限，y的值随x的值增大而减小．
22、4
【解析】
首先由对边分别平行可判断四边形ABCD为平行四边形，连接AC和BD，过A点分别作DC和BC的垂线，垂足分别为F和E，通过证明△ADF≌△ABC来证明四边形ABCD为菱形，从而得到AC与BD相互垂直平分，再利用勾股定理求得BD长度.
【详解】
解：连接AC和BD，其交点为O，过A点分别作DC和BC的垂线，垂足分别为F和E，
∵AB∥CD，AD∥BC，
∴四边形ABCD为平行四边形，
∴∠ADF=∠ABE，
∵两纸条宽度相同，
∴AF=AE，
∵
∴△ADF≌△ABE，
∴AD=AB，
∴四边形ABCD为菱形，
∴AC与BD相互垂直平分，
∴BD=
故本题答案为：4
本题考察了菱形的相关性质，综合运用了三角形全等和勾股定理，注意辅助线的构造一定要从相关条件以及可运用的证明工具入手，不要盲目作辅助线.
23、1
【解析】
因为关于的一元二次方程有两个相等的实数根，故 ，代入求解即可.
【详解】
根据题意可得： 解得：m=1
故答案为：1
本题考查的是一元二次方程的根的判别式，掌握根的判别式与方程的根的关系是关键.
二、解答题（本大题共3个小题，共30分）
24、（1）见解析；（2）见解析；（3）
【解析】
（1）利用尺规作出∠ABC的角平分线即可．
（2）利用尺规作出线段BD的垂直平分线即可．
（3）根据等腰三角形的定义判断即可．
【详解】
（1）射线BD即为所求．
（2）直线EF即为所求．
（3）△BDE，△BDF，△BEF是等腰三角形．
本题考查作图-复杂作图，线段的垂直平分线，角平分线的定义等知识，解题的关键是熟练掌握基本知识.
25、（1） 见解析；（2）15，15；（3）人均年收入为15.1万元.
【解析】
（1）从两个统计图中得到C组15万元的有20人，占调查人数的40%，可求出调查人数，进而得到D组人数，补全条形统计图，
（2）根据中位数、众数的意义和求法分别求出即可，排序后求出第25、26位的两个数的平均数即为中位数，出现次数最多的数是众数，
（3）利用平均数的计算公式进行计算．
【详解】
解：（1）20÷40%=50人，50-3-11-20-2=14人，补全条形统计图如图所示：
（2）员工年收入在15万元出现次数最多是20次，因此众数是15万，
调查50人的收入从小到大排列后处在第25、26位的数据都是15万，因此中位数是15万，
（3）=15.1万元，
答：该公司员工人均年收入约为15.1万元．
本题考查条形统计图、扇形统计图的制作方法、平均数、中位数、众数的意义，理解统计图中各个数据之间的关系是解决问题的关键．
26、（1）40；（2）50，40；（3）1200人
【解析】
（1）根据平均数的定义即可列式求解；
（2）根据表格即可求出众数、中位数；
（3）先求出捐款40元以上（包括40元）的人数占比，再乘以总人数即可求解.
【详解】
（1）设被污染处的数据钱数为x,
故
解得x=40；
（2）由表格得众数为50，第25,26位同学捐的钱数为40，故中位数为40；
（3）解：全校捐款40元以上（包括40元）的人数为（人）
此题主要考查统计调查的应用，解题的关键是熟知平均数、中位线、众数的定义.
题号
一
二
三
四
五
总分
得分
批阅人
选手
甲
乙
丙
丁
平均环数
9
9.5
9
9.5
方差
4.5
4
4
5.4
x/cm
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
y/cm
0
0.4
0.8
1.2
1.6
1.7
1.6
1.2
0
进价（元/件）
售价（元/件）
甲种商品
乙种商品
捐款（元）
10
15
30
50
60
人数
3
6
11
11
13
6
x/cm
0
0.5
1
1.5
2
2.5
3
3.5
1
1.5
y/cm
0
0.1
0.8
1.2
1.1
1.6
1.7
1.6
1.2
0