山东省临沂市莒南县2023-2024学年八年级上期中数学试卷及答案

这是一份山东省临沂市莒南县2023-2024学年八年级上期中数学试卷及答案，共8页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

一、选择题（每小题3分，共42分）将唯一正确答案的代号字母填在下面的方格内
1．以下列各组线段为边，能组成三角形的是（ ）
2．（3分）如图，下列汉字中近似为轴对称图形的有（ ）
3．一个多边形的内角和是外角和的2倍，则这个多边形的边数为（ ）
4．过多边形的一个顶点的所有对角线把多边形分成8个三角形，这个多边形的边数是（ ）
5． n边形的每个外角都为24°，则边数n为（ ）
6．已知等腰三角形的两边长分别是3和6，则它的周长等于（ ）
7．将一张长方形纸片只折一次，使得折痕平分这个长方形的面积，这样的方法共有（ ）
8．点M（1，2）关于y轴对称点的坐标为（ ）
9．下列图形中对称轴最多的是（ ）
10．如图，a、b、c分别表示△ABC的三边长，则下面与△ABC一定全等的三角形是（ ）
11．如图，在△ABC和△A′B′C′中，AB=A′B′，∠B=∠B′，补充条件后仍不一定能保证△ABC≌△A′B′C′，则补充的这个条件是（ ）
12．如图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（ ）

第12题图 第13题图
13．要测量河两岸相对的两点A，B的距离，先在AB的垂线BF上取两点C，D，使CD=BC，再定出BF的垂线DE，使A，C，E在一条直线上（如图所示），可以说明△EDC≌△ABC，得ED=AB，因此测得ED的长就是AB的长，判定△EDC≌△ABC最恰当的理由是（ ）
14．如图，在△ABC中，AB=AC，∠ABC、∠ACB的平分线BD，CE相交于O点，且BD交AC于点D，CE交AB于点E．某同学分析图形后得出以下结论：①△BCD≌△CBE；②△BAD≌△BCD；③△BDA≌△CEA；④△BOE≌△COD；⑤△ACE≌△BCE；上述结论一定正确的是（ ）

第14题图 第16题图 第17题图
二、填空题：（每题3分，共15分）答案直接填在题中的横线上。
15．点M（a，﹣5）与点N（﹣2，b）关于x轴对称，则a+b= _________ ．
16．如图为6个边长等的正方形的组合图形，则∠1+∠2+∠3= _________ °．
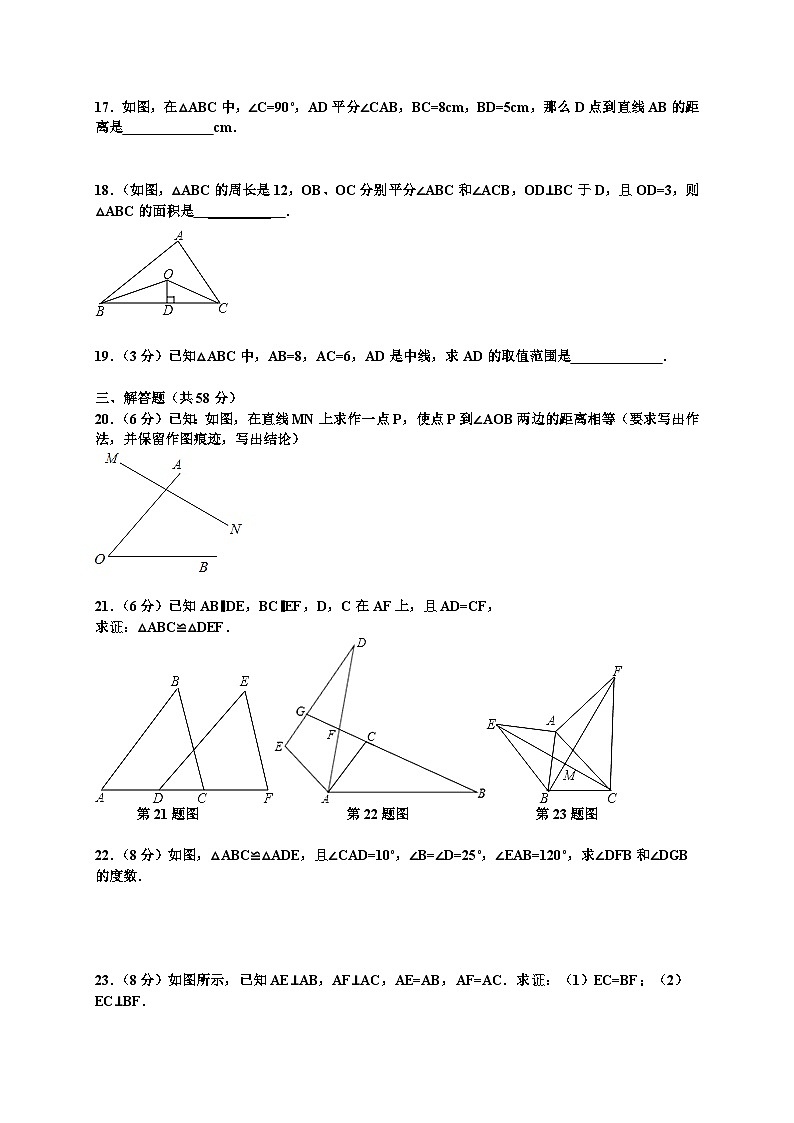
17．如图，在△ABC中，∠C=90°，AD平分∠CAB，BC=8cm，BD=5cm，那么D点到直线AB的距离是 _________ cm．

18．（如图，△ABC的周长是12，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，则△ABC的面积是 _________ ．

19．（3分）已知△ABC中，AB=8，AC=6，AD是中线，求AD的取值范围是 _________ ．

三、解答题（共58分）
20．（6分）已知：如图，在直线MN上求作一点P，使点P到∠AOB两边的距离相等（要求写出作法，并保留作图痕迹，写出结论）
21．（6分）已知AB∥DE，BC∥EF，D，C在AF上，且AD=CF，
求证：△ABC≌△DEF．
第21题图 第22题图 第23题图
22．（8分）如图，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数．

23．（8分）如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC．求证：（1）EC=BF；（2）EC⊥BF．

24．（10分）如图，写出△ABC各顶点的坐标，并画出△ABC关于x轴对称的△DEF，你能证明AC=BC吗？

25．（8分）如图，E在△ABC的AC边的延长线上，D点在AB边上，DE交BC于点F，DF=EF，BD=CE，求证：△ABC是等腰三角形．
26．（12分）（1）如图（1），把三角形纸片ABC的角A沿DE折起（DE为折痕），使顶点A在∠A的内部，点A的对称点为点O，判断∠O、∠ODC、∠BEO的大小关系，并写出证明过程．
（2）如图（2），把三角形纸片ABC的角A沿DE折起（DE为折痕），使顶点A在∠A的外部，点A的对称点为点O，判断∠O、∠ODC、∠BEO的大小关系吗？（只写出答案，无需证明）．
（3）在图（1）的基础上再以FG为折痕叠纸片，形成如图（3）的形状．判断∠1、∠2、∠3、∠4、∠5、∠6、∠7的之间大小关系吗？（只写出答案，无需证明）．

参考答案

一、选择题（每小题3分，共42分）将唯一正确答案的代号字母填在下面的方格内
1．D
2．B
3．C
4．C
5．C
6．D
7．D
8．A
9．A
10．B
11．C
12．D
13．B
14．D
二、填空题：（每题3分，共15分）答案直接填在题中的横线上。
15． 3 ．
16． 135 °．
17． 3 cm．
18． 18 ．
19． 1＜AD＜7 ．
三、解答题（共58分）

A．
2cm，3cm，5cm
B．
3cm，3cm，6cm
C．
2cm，5cm，8cm
D．
4cm，5cm，6cm

A．
1个
B．
2个
C．
3个
D．
4个

A．
4
B．
5
C．
6
D．
7

A．
8
B．
9
C．
10
D．
11

A．
13
B．
14
C．
15
D．
16

A．
12
B．
12或15
C．
15或18
D．
15

A．
2种
B．
4种
C．
6种
D．
无数种

A．
（﹣1，2）
B．
（﹣1，﹣2）
C．
（1，﹣2）
D．
（2，﹣1）

A．
圆
B．
正方形
C．
等腰三角形
D．
线段

A．
BC=B′C′
B．
∠A=∠A′
C．
AC=A′C′
D．
∠C=∠C′

A．
△ACE≌△BCD
B．
△BGC≌△AFC
C．
△DCG≌△ECF
D．
△ADB≌△CEA

A．
边角边
B．
角边角
C．
边边边
D．
边边角

A．
①②③
B．
②③④
C．
①③⑤
D．
①③④
解：延长AD至点E，使DE=AD，连接EC，
∵BD=CD，DE=AD，∠ADB=∠EDC，
∴△ABD≌△ECD，∴CE=AB，
∵AB=8，AC=6，CE=8，
设AD=x，则AE=2x，
∴2＜2x＜14，
∴1＜x＜7，
∴1＜AD＜7．
20．
解：作∠AOB的平分线，∠AOB的平分线与直线MN交于一点，
如图所示：点P即为所求．
21．
证明：∵AB∥DE，BC∥EF
∴∠A=∠EDF，∠F=∠BCA
又∵AD=CF
∴AC=DF
∴△ABC≌△DEF．（ASA）
22．
解：∵△ABC≌△ADE，
∴∠DAE=∠BAC=（∠EAB﹣∠CAD）=．
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB﹣∠D=90°﹣25°=65°．
23．
证明：（1）∵AE⊥AB，AF⊥AC，
∴∠BAE=∠CAF=90°，
∴∠BAE+∠BAC=∠CAF+∠BAC，
即∠EAC=∠BAF，
在△ABF和△AEC中，
∵，
∴△ABF≌△AEC（SAS），
∴EC=BF；
（2）如图，根据（1），△ABF≌△AEC，
∴∠AEC=∠ABF，
∵AE⊥AB，
∴∠BAE=90°，
∴∠AEC+∠ADE=90°，
∵∠ADE=∠BDM（对顶角相等），
∴∠ABF+∠BDM=90°，
在△BDM中，∠BMD=180°﹣∠ABF﹣∠BDM=180°﹣90°=90°，
所以EC⊥BF．
24．
解：如图：A（﹣3，2），B（﹣4，﹣3），C（﹣1，﹣1）；
△DEF即为所求；
AC=BC．
证明：∵AC==，BC==，
∴AC=BC．
25．
证明：过点D作DG∥AE于点G，
∵DG∥AC
∴∠GDF=∠CEF（两直线平行，内错角相等），
在△GDF和△CEF中
，
∴△GDF≌△CEF（ASA），
∴DG=CE
又∵BD=CE，
∴BD=DG，
∴∠DBG=∠DGB，
∵DG∥AC，
∴∠DGB=∠ACB，
∴∠ABC=∠ACB，
∴△ABC是等腰三角形．
26．
解：（1）2∠O=∠ODC+∠BEO．理由如下：
如图1，∵把三角形纸片ABC的角A沿DE折起，点A的对称点为点O，
∴∠A=∠O，∠ADE=∠ODE，∠AED=∠OED．
∵∠O+∠ODE+∠OED=180°，
∠ODC+∠ODE+∠EDA=180°，
∠BEO+∠DEO+∠AED=180°，
∴2∠O=360°﹣2∠0DE﹣2∠OED，
∠ODC=180°﹣2∠ODE，
∠BEO=180°﹣2∠OED，
∴2∠O=∠ODC+∠BEO；
（2）2∠O=∠ODC﹣∠BEO．理由如下：
如图2，设DO交AB于点F，
∵∠ODC=∠A+∠DFA，∠DFA=∠O+∠BEO，
∴∠ODC=∠A+∠O+∠BEO，
∴∠ODC﹣∠BEO=∠A+∠O，
∵△ODE是由△ADE沿直线DE折叠而得，
∴∠A=∠O，
∴2∠O=∠ODC﹣∠BEO；
（3）∠1+∠3+∠5+∠7=∠2+2∠4+∠6或∠1+∠3+∠5+∠7=4∠4．理由如下：
如图3，由（1）的结论及折叠的性质可知，2∠4=∠2+∠6，2∠6=∠5+∠7，2∠2=∠1+∠3，
∴∠1+∠3+∠5+∠7+∠2+∠6=2∠2+2∠6+2∠4，
∴∠1+∠3+∠5+∠7=∠2+2∠4+∠6，
∵2∠4=∠2+∠6，
∴∠1+∠3+∠5+∠7=4∠4．