河南省汤阴县2025届九年级数学第一学期开学经典模拟试题【含答案】

这是一份河南省汤阴县2025届九年级数学第一学期开学经典模拟试题【含答案】，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
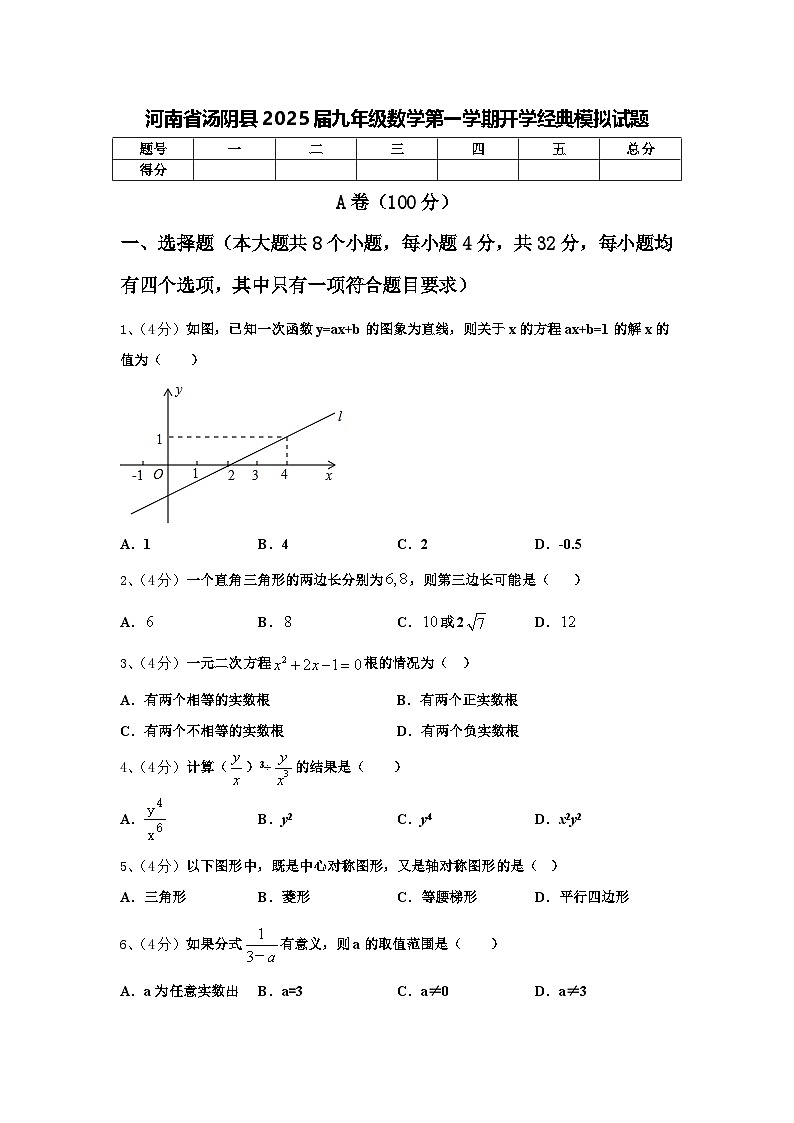
1、（4分）如图，已知一次函数y=ax+b的图象为直线，则关于x的方程ax+b=1的解x的值为（ ）
A．1B．4C．2D．-0.5
2、（4分）一个直角三角形的两边长分别为，则第三边长可能是（ ）
A．B．C．或2D．
3、（4分）一元二次方程根的情况为（ ）
A．有两个相等的实数根B．有两个正实数根
C．有两个不相等的实数根D．有两个负实数根
4、（4分）计算（）3÷的结果是（ ）
A．B．y2C．y4D．x2y2
5、（4分）以下图形中，既是中心对称图形，又是轴对称图形的是（ ）
A．三角形B．菱形C．等腰梯形D．平行四边形
6、（4分）如果分式有意义，则a的取值范围是（ ）
A．a为任意实数出B．a=3C．a≠0D．a≠3
7、（4分）有位同学参加歌咏比赛，所得的分数互不相同，取得分前位同学进入决赛，小明知道自己的分数后，要判断自己能否进入决赛，他只需知道这位同学得分的（ ）
A．平均数B．中位数C．众数D．方差
8、（4分）某体育馆准备重新铺设地面，已有一部分正三角形的地砖，现要购买另一种不同形状的正多边形地砖与正三角形在同一顶点处作平面镶嵌（正多边形的边长相等），则该体育馆不应该购买的地砖形状是（ ）
A．正方形B．正六边形C．正八边形D．正十二边形
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）为了考察甲、乙两块地小麦的长势，分别从中随机抽出10株苗，测得苗高如图所示．若和 分别表示甲、乙两块地苗高数据的方差，则________．(填“>”、“<”或“=”)．
10、（4分）已知函数y＝（m﹣1）x+m2﹣1是正比例函数，则m＝_____．
11、（4分）如图，已知等边△ABC的边长为10，P是△ABC内一点，PD平行AC，PE平行AD，PF平行BC，点D，E，F分别在AB，BC，AC上，则PD+PE+PF= _______________．
12、（4分）一组数据3，2，4，5，2的众数是______．
13、（4分）甲、乙两家人，相约周末前往中梁国际慢城度周末，甲、乙两家人分别从上桥和童家桥驾车同时出发，匀速前进，且甲途经童家桥，并以相同的线路前往中梁国际慢城. 已知乙的车速为30千米/小时，设两车之间的里程为y（千米），行驶时间为x（小时），图中的折线表示从两家人出发至甲先到达终点的过程中y（千米）与x（小时）的函数关系，根据图中信息，甲的车速为_______千米/小时.
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在△ABC中，∠BAC=90°，AD是中线，E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF，求证：四边形ADCF是菱形．
15、（8分）如图所示，AE是∠BAC的角平分线，EB⊥AB于B，EC⊥AC于C，D是AE上一点，求证：BD=CD．
16、（8分）如图1，□ABCD的顶点A，B，D的坐标分别是（2，0），（6，0），D（0，t），t＞0，作▱ABCD关于直线CD对称的□A'B'CD，其中点A的对应点是点A'、点B的对应点是点B'．
（1）请你在图1中画出▱A′B′CD，并写出点A′的坐标；（用含t的式子表示）
（2）若△OA′C的面积为9，求t的值；
（3）若直线BD沿x轴的方向平移m个单位长度恰好经过点A′，求m的值．
17、（10分）一个有进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分钟进水量和出水量是两个常数．容器内的水量y(单位：L)与时间x(单位：min)之间的关系如图所示．
(1)求y关于x的函数解析式；
(2)每分钟进水、出水各多少升？
18、（10分）求不等式（2x﹣1）（x+1）＞0的解集．
解：根据“同号两数相乘，积为正”可得：①或 ②．
解①得x＞；解②得x＜﹣1．
∴不等式的解集为x＞或x＜﹣1．
请你仿照上述方法解决下列问题：
（1）求不等式（2x﹣1）（x+1）＜0的解集．
（2）求不等式≥0的解集．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，在平面直角坐标系xOy中，菱形AOBC的边长为8，∠AOB=60°． 点D是边OB上一动点，点E在BC上，且∠DAE=60°．
有下列结论：
①点C的坐标为（12，）；②BD=CE；
③四边形ADBE的面积为定值；
④当D为OB的中点时，△DBE的面积最小．
其中正确的有_______．（把你认为正确结论的序号都填上）
20、（4分）分解因式：_____.
21、（4分）如图，在平行四边形 ABCD 中， AD  2 AB ；CF 平分 BCD 交 AD 于 F ，作 CE  AB ， 垂足 E 在边 AB 上，连接 EF ．则下列结论：① F 是 AD 的中点； ② S△EBC  2S△CEF；③ EF  CF ； ④ DFE  3AEF ．其中一定成立的是_____．（把所有正确结论的序号都填在横线上）
22、（4分）用反证法证明命题“在直角三角形中，至少有一个锐角不大于 45°”时第一步先假设所求证的结论不成立，即问题表述为______．
23、（4分）一次函数，若y随x的增大而增大，则的取值范围是 .
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，点A在的边ON上，于点B，，于点E，，于点C．
求证：四边形ABCD是矩形.
25、（10分）如图，在□ABCD中，∠ABC的平分线交AD于点E，延长BE交CD的延长线于点F.
(1)若∠F＝20°，求∠A的度数；
(2)若AB＝5，BC＝8，CE⊥AD，求□ABCD的面积．
26、（12分）如图，直线y1＝2x－2的图像与y轴交于点A，直线y2＝－2x＋6的图像与y轴交于点B，两者相交于点C．
(1)方程组的解是______；
(2)当y1＞0与y2＞0同时成立时，x的取值范围为_____；
(3)求△ABC的面积；
(4)在直线y1＝2x－2的图像上存在异于点C的另一点P，使得△ABC与△ABP的面积相等，请求出点P的坐标．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
根据一次函数图象可得一次函数y=ax+b的图象经过(4，1)点，进而得到方程的解．
【详解】
根据图象可得，一次函数y=ax+b的图象经过(4，1)点，
因此关于x的方程ax+b=1的解x=4，
故选B．
本题考查了一次函数与方程，关键是正确利用数形结合的方法从图象中找到正确答案．
2、C
【解析】
本题已知直角三角形的两边长，但未明确这两条边是直角边还是斜边，因此两条边中的较长边8既可以是直角边，也可以是斜边，所以求第三边的长必须分类讨论，即8是斜边或直角边的两种情况，然后利用勾股定理求解．
【详解】
解：设第三边为x，
①当8是直角边，则62+82=x2解得x=10，
②当8是斜边，则62+x2=82，解得x=2 ．
∴第三边长为10或2．
故选：C．
本题考查了利用勾股定理解直角三角形的能力，当已知条件中没有明确哪是斜边时，要注意讨论，一些学生往往忽略这一点，造成丢解．
3、C
【解析】
根据方程的系数结合根的判别式，可得出△=8＞0，由此即可得出原方程有两个不相等的实数根．
【详解】
解：∵在方程x2+2x-1=0中，△=22-4×1×（-1）=8＞0，
∴方程x2+2x-1=0有两个不相等的实数根．
故选：C．
本题考查根的判别式，牢记“当△＞0时，方程有两个不相等的实数根”是解题的关键．
4、B
【解析】
根据分式的运算法则即可求出答案．
【详解】
解：原式＝
＝
= ，
故选：B．
此题考查分式的运算及幂的运算，难度一般．
5、B
【解析】
关于某条直线对称的图形叫轴对称图形．绕一个点旋转180度后所得的图形与原图形完全重合的图形叫做中心对称图形．
【详解】
解：A、三角形既不是中心对称图形，也不是轴对称图形；
B、菱形既是中心对称图形，也是轴对称图形；
C、等腰梯形是轴对称图形；
D、平行四边形是中心对称图形.
故选B.
掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后两部分重合．
6、D
【解析】
直接利用分式的分母不等于0，进而得出答案．
【详解】
解：分式有意义，则，
解得：．
故选：D．
此题主要考查了分式有意义的条件，正确把握定义是解题关键．
7、B
【解析】
由中位数的概念，即最中间一个或两个数据的平均数；可知9人成绩的中位数是第5名的成绩．根据题意可得：参赛选手要想知道自己是否能进入前5名，只需要了解自己的成绩以及全部成绩的中位数，比较即可．
【详解】
解：由于9个人中，第5名的成绩是中位数，故小明同学知道了自己的分数后，想知道自己能否进入决赛，需知道这9位同学的分数的中位数．
故选：B．
此题主要考查统计的有关知识，主要包括平均数、中位数、众数的意义．反映数据集中程度的统计量有平均数、中位数、众数等，各有局限性，因此要对统计量进行合理的选择和恰当的运用．
8、C
【解析】
根据密铺的条件得，两多边形内角和必须凑出，进而判断即可．
【详解】
解：、正方形的每个内角是，，能密铺；
、正六边形每个内角是，，能密铺；
、正八边形每个内角是，与无论怎样也不能组成的角，不能密铺；
、正十二边形每个内角是，，能密铺．
故选：C．
本题考查两种正多边形的镶嵌应符合多个内角度数和等于．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、<
【解析】
方差用来计算每一个变量（观察值）与总体均数之间的差异，所以从图像看苗高的波动幅度，可以大致估计甲、乙两块地苗高数据的方差.
【详解】
解：由图可知，甲、乙两块地的苗高皆在12cm上下波动，但乙的波动幅度比甲大，
∴ 则
故答案为：<
本题考查了方差，方差反映了数据的波动程度，方差越大，数据的波动越大，正确理解方差的含义是解题的关键.
10、-2
【解析】
由正比例函数的定义可得m2﹣2＝2，且m﹣2≠2．
【详解】
解：由正比例函数的定义可得：m2﹣2＝2，且m﹣2≠2，
解得：m＝﹣2，
故答案为：﹣2．
本题考查了正比例函数的定义．解题关键是掌握正比例函数的定义条件：正比例函数y＝kx的定义条件是：k为常数且k≠2．
11、1
【解析】
延长EP、FP分别交AB、BC于G、H，则由PD∥AB，PE∥BC，PF∥AC，可得平行四边形PGBD和平行四边形EPHC，再根据平行四边形及等边三角形的性质得到PD=DH,PE=HC,PF=BD，故可求出PD+PE+PF的长．
【详解】
如图，延长EP、FP分别交AB、BC于G、H，
由PD∥AB，PE∥BC，PF∥AC，可得平行四边形PGBD和平行四边形EPHC，
∴PG=BD,PE=HC
又∵△ABC是等边三角形，
且PF∥AC，PD∥AB，可得△PFG，△PDH是等边三角形，
∴PF=PG=BD,PD=DH
∴PD+PE+PF=DH+GP+HC=DH+BD+HC=BC=1
故答案为：1．
此题主要考查平行四边形的判定与性质，解题的关键是熟知平行四边形的性质及等边三角形的判定与性质．
12、1
【解析】
从一组数据中找出出现次数最多的数就是众数，发现1出现次数最多，因此1是众数．
【详解】
解：出现次数最多的是1，因此众数是1，
故答案为：1．
本题考查了众数的意义，从一组数据中找到出现次数最多的数就是众数．
13、1
【解析】
根据题意和函数图象可知，甲小时行驶的路程=乙小时行驶的路程+10，从而可以求得甲的车速．
【详解】
解：由题意可得，
甲的车速为：千米/小时，
故答案为1．
本题考查一次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
三、解答题（本大题共5个小题，共48分）
14、见解析
【解析】
根据AAS证△AFE≌△DBE，推出AF=BD．结合已知条件，利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是平行四边形，进而证明ADCF是菱形．
【详解】
证明：∵AF∥BC，
∴∠AFE=∠DBE，
∵E是AD的中点，AD是BC边上的中线，
∴AE=DE，BD=CD，
在△AFE和△DBE中，
，
∴△AFE≌△DBE（AAS）；
∴AF=DB．
∵DB=DC，
∴AF=CD．
∵AF∥BC，
∴四边形ADCF是平行四边形，
∵∠BAC=90°，D是BC的中点，E是AD的中点，
∴AD=BC=DC，
∴四边形ADCF是菱形．
本题考查了全等三角形的性质和判定，平行四边形的判定，菱形的判定的应用，解题的关键是正确寻找全等三角形，利用直角三角形的性质解决问题，属于中考常考题型．
15、见解析
【解析】
求出EC=EB，∠ECA=∠EBA=90°，∠CAE=∠BAE，根据AAS推出△CAE≌△BAE，根据全等三角形的性质得出AC=AB，根据SAS推出△CAD≌△BAD即可．
【详解】
证明：∵AE是∠BAC的角平分线，EB⊥AB，EC⊥AC，
∴EC=EB，∠ECA=∠EBA=90°，∠CAE=∠BAE，
在△CAE和△BAE中
,
∴△CAE≌△BAE，
∴AC=AB，
在△CAD和△BAD中
,
∴△CAD≌△BAD，
∴BD=CD．
考查了全等三角形的性质和判定的应用，注意：全等是三角形的对应边相等，对应角相等．
16、（1）▱A′B′CD如图所示见解析，A′（2，2t）；（2）t＝3；（3）m＝1．
【解析】
（1）根据题意逐步画出图形.（2）根据三角形的面积计算方式进行作答.（3）根据平移的相关性质进行作答.
【详解】
（1）▱A′B′CD如图所示，A′（2，2t）．
（2）∵C′（4，t），A（2，0），
∵S△OA′C＝10t﹣×2×2t﹣×6×t﹣×4×t＝2．
∴t＝3．
（3）∵D（0，t），B（6，0），
∴直线BD的解析式为y＝﹣x＋t，
∴线BD沿x轴的方向平移m个单位长度的解析式为y＝﹣x＋（6＋m），
把点A（2，2t）代入得到，2t＝﹣＋t＋，
解得m＝1．
本题主要考查了三角形的面积计算方式及平移的相关性质，熟练掌握三角形的面积计算方式及平移的相关性质是本题解题关键.
17、（1）；（2）每分钟进水、出水各5L，L．
【解析】
（1）根据题意和函数图象可以求得y与x的函数关系式；
（2）根据函数图象中的数据可以求得每分钟进水、出水各多少升．
【详解】
解：（1）当0≤x≤4时，设y关于x的函数解析式是y＝kx，
4k＝20，得k＝5，
即当0≤x≤4时，y与x的函数关系式为y＝5x，
当4＜x≤12时，设y与x的函数关系式为y＝ax+b，
，得，
即当4≤x≤12时，y与x的函数关系式为，
由上可得，；
（2）进水管的速度为：20÷4＝5L/min，
出水管的速度为： L/min，
答：每分钟进水、出水各5L， L．
本题考查一次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
18、（1）﹣1＜x＜；（2）x≥1或x＜﹣2．
【解析】
（1）、（2）根据题意得出关于x的不等式组，求出x的取值范围即可．
【详解】
解：（1）根据“异号两数相乘，积为负”可得①或②，
解①得不等式组无解；解②得，﹣1＜x＜；
（2）根据“同号两数相除，积为正”可得①，②，
解①得，x≥1，解②得，x＜﹣2，
故不等式组的解集为：x≥1或x＜﹣2．
故答案为（1）﹣1＜x＜；（2）x≥1或x＜﹣2．
本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、①②③
【解析】
①过点C作CF⊥OB，垂足为点F，求出BF=4，CF=，即可求出点C坐标；②连结AB，证明△ADB≌△AEC，则BD=CE；③由S△ADB=S△AEC，可得S△ABC=S△四边形ADBE=×8×=；④可证△ADE为等边三角形，当D为OB的中点时，AD⊥OB，此时AD最小，则S△ADE最小，由③知S四边形ADBE为定值，可得S△DBE最大．
【详解】
解：①过点C作CF⊥OB，垂足为点F，
∵四边形AOBC为菱形，
∴OB=BC=8，∠AOB=∠CBF=60°，
∴BF=4，CF=，
∴OF=8+4=12，
∴点C的坐标为（12，），故①正确；
②连结AB，
∵BC=AC=AO=OB，∠AOB=∠ACB=60°，
∴△ABC是等边三角形，△AOB是等边三角形，
∴AB=AC，∠BAC=60°，
∵∠DAE=60°，
∴∠DAB=∠EAC，
∵∠ABD=∠ACE=60°，
∴△ADB≌△AEC（ASA），
∴BD=CE，故②正确；
③∵△ADB≌△AEC．
∴S△ADB=S△AEC，
∴S△ABC=S△四边形ADBE=×8×=，故③正确；
④∵△ADB≌△AEC，
∴AD=AE，
∵∠DAE=60°，
∴△ADE为等边三角形，
当D为OB的中点时，AD⊥OB，
此时AD最小，则S△ADE最小，
由③知S四边形ADBE为定值，可得S△DBE最大．
故④不正确；
故答案为：①②③．
本题考查了菱形的性质，全等三角形的判定与性质，等边三角形的判定与性质等，正确作出辅助线是解题的关键．
20、
【解析】
直接提取公因式a即可得答案.
【详解】
3a2+a=a(3a+1)，
故答案为：a(3a+1)
本题考查提取公因式法分解因式，正确找出公因式是解题关键.
21、①③④.
【解析】
由角平分线的定义和平行四边形的性质可证得CD=DF，进一步可证得F为AD的中点，由此可判断①；延长EF，交CD延长线于M，分别利用平行四边形的性质以及①的结论可得△AEF≌△DMF，结合直角三角形的性质可判断③；结合EF=FM，利用三角形的面积公式可判断②；在△DCF和△ECF中利用等腰三角形的性质、外角的性质及三角形内角和可得出∠DFE=3∠AEF，可判断④，综上可得答案.
【详解】
解：∵四边形ABCD为平行四边形，∴AD∥BC，
∴∠DFC=∠BCF，
∵CF平分∠BCD，∴∠BCF=∠DCF，
∴∠DFC=∠DCF，∴CD=DF，
∵AD=2AB， ∴AD=2CD，
∴AF=FD=CD，即F为AD的中点，故①正确；
延长EF，交CD延长线于M，如图，

∵四边形ABCD是平行四边形， ∴AB∥CD，
∴∠A=∠MDF，
∵F为AD中点，∴AF=FD，
又∵∠AFE=∠DFM，
∴△AEF≌△DMF（ASA），
∴FE=MF，∠AEF=∠M，
∵CE⊥AB，∴∠AEC=90°，
∴∠ECD=∠AEC=90°，
∵FM=EF，∴FC=FM，故③正确；
∵FM=EF，∴，
∵MC＞BE，
∴＜2，故②不正确；
设∠FEC=x，则∠FCE=x，
∴∠DCF=∠DFC=90°－x，
∴∠EFC=180°－2x，
∴∠EFD=90°－x+180°－2x=270°－3x ，
∵∠AEF=90°－x，
∴∠DFE=3∠AEF，故④正确；
综上可知正确的结论为①③④.
故答案为①③④.
本题以平行四边形为载体，综合考查了平行四边形的性质、全等三角形的判定和性质、直角三角形的斜边上的中线等于斜边一半的性质、三角形的内角和和等腰三角形的判定和性质，思维量大，综合性强. 解题的关键是正确作出辅助线，综合运用所学知识去分析思考；本题中见中点，延长证全等的思路是添辅助线的常用方法，值得借鉴与学习.
22、假设在直角三角形中，两个锐角都大于45°.
【解析】
反证法的第一步是假设命题的结论不成立，据此可以得出答案.
【详解】
∵反证法的第一步是假设命题的结论不成立，∴用反证法证明命题“在直角三角形中，至少有一个锐角不大于 45°”时第一步即为，假设在直角三角形中，两个锐角都大于45°.
此题主要考查了反证法的知识，解此题的关键是掌握反证法的意义和步骤. 反证法的步骤是：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）由矛盾说明假设错误，从而证明原命题正确.
23、．
【解析】
一次函数的图象有两种情况：
①当时，函数的值随x的值增大而增大；
②当时，函数的值随x的值增大而减小．
由题意得，函数的y随x的增大而增大，．
二、解答题（本大题共3个小题，共30分）
24、详见解析
【解析】
根据全等三角形的判定和性质以及矩形的判定解答即可；
【详解】
证明：（证法不唯一）∵于点B，于点E，
∴.
在与中，
∵
∴．
∴，
∴．
又∵，，
∴．
∴四边形ABCD是平行四边形.
∵，
∴四边形ABCD是矩形．
此题考查了矩形的判定与性质以及勾股定理．
25、 (1) 140°；(2) S▱ABCD＝32.
【解析】
(1)∵四边形ABCD是平行四边形，
∴AD∥BC,AD=BC=8,CD=AB=5,AB∥CD，

∵∠ABC的平分线交AD于点E，
∴∠ABE=∠CBF，


(2)∵AE=AB=5，AD=BC=8，CD=AB=5，
∴DE=AD−AE=3，
∵CE⊥AD，

∴▱ABCD的面积=AD⋅CE=8×4=32.
26、 (1) ;(2) 1＜x＜3;(3)8;(4) P(－2，－6)
【解析】
（1）根据图像可知，两条直线的交点即为方程组的解；（2）找出两条直线的图像在x轴上方的公共部分的x的取值范围即可；（3）令x=0，求出y1与y2的值，即可得A、B两点的坐标，进而可得AB的长度，根据C点坐标为（2，2），可得△ABC的高，即可求出面积；（4）令P(x0，2x0－2)，根据三角形面积公式可得x0＝±2，由点P异于点C可得x0＝－2，代入y1＝2x－2即可的P点坐标.
【详解】
（1）由图像可知直线y1＝2x－2的图像与直线y2＝－2x＋6的交点坐标为（2，2）
∴方程组的解集为，
（2）根据图像可知：当y1＞0与y2＞0同时成立时，x的取值范围为1＜x＜3.
(3)∵令x＝0，则y1＝－2，y2＝6，
∴A(0，－2)，B(0，6)．
∴AB＝8.
∴S△ABC＝×8×2＝8.
(4)令P(x0，2x0－2)，则S△ABP＝×8×|x0|＝8，
∴x0＝±2.
∵点P异于点C，
∴x0＝－2，2x0－2＝－6.
∴P(－2，－6)．
此题考查了一次函数综合题，涉及的知识有：一次函数与坐标轴的交点，坐标与图形性质，三角形面积，以及两一次函数的交点， 熟练掌握一次函数图像的特征是解题关键.
题号
一
二
三
四
五
总分
得分