贵州省毕节市2024年数学九上开学监测试题【含答案】

这是一份贵州省毕节市2024年数学九上开学监测试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）教练要从甲、乙两名射击运动员中选一名成绩较稳定的运动员参加比赛．两人在形同条件下各打了5发子弹，命中环数如下：甲：9、8、7、7、9；乙：10、8、9、7、1．应该选（ ）参加．
A．甲B．乙C．甲、乙都可以D．无法确定
2、（4分）实数a,b在数轴上的位置如图所示,则化简代数式|a+b|−a的结果是( )
A．2a+bB．2aC．aD．b
3、（4分）环保部门根据我市一周的检测数据列出下表.这组数据的中位数是
A．B．C．D．
4、（4分）下列计算正确的是（ ）
A．B．2C．（）2＝2D．＝3
5、（4分）甲、乙两个同学在四次数学模拟测试中，平均成绩都是112分，方差分别是s＝5，s＝12，则甲、乙两个同学的数学成绩比较稳定的是（ ）.
A．甲B．乙C．甲和乙一样D．无法确定
6、（4分）如图，正方形ABCD的四个顶点A、B、C、D正好分别在四条平行线l1、l2、l3、l4上．若从上到下每两条平行线间的距离都是2cm，则正方形ABCD的面积为（ ）
A．4cm2B．5cm2C．20cm2D．30cm2
7、（4分）如图，菱形中，，与交于，为延长线上的一点，且，连结分别交，于点，，连结则下列结论：①；②与全等的三角形共有个；③；④由点，，，构成的四边形是菱形．其中正确的是（ ）
A．①④B．①③④C．①②③D．②③④
8、（4分）如果分式有意义，那么x的取值范围是（ ）
A．x≠0B．x≤﹣3C．x≥﹣3D．x≠﹣3
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，在△ABC中，∠B=∠C=60°，点D在AB边上，DE⊥AB，并与AC边交于点E．如果AD=1，BC=6，那么CE等于______．
10、（4分）菱形的周长为12，它的一个内角为60°，则菱形的较长的对角线长为______．
11、（4分）已知一组数据6，x，3，3，5，1的众数是3和5，则这组数据的中位数是_____．
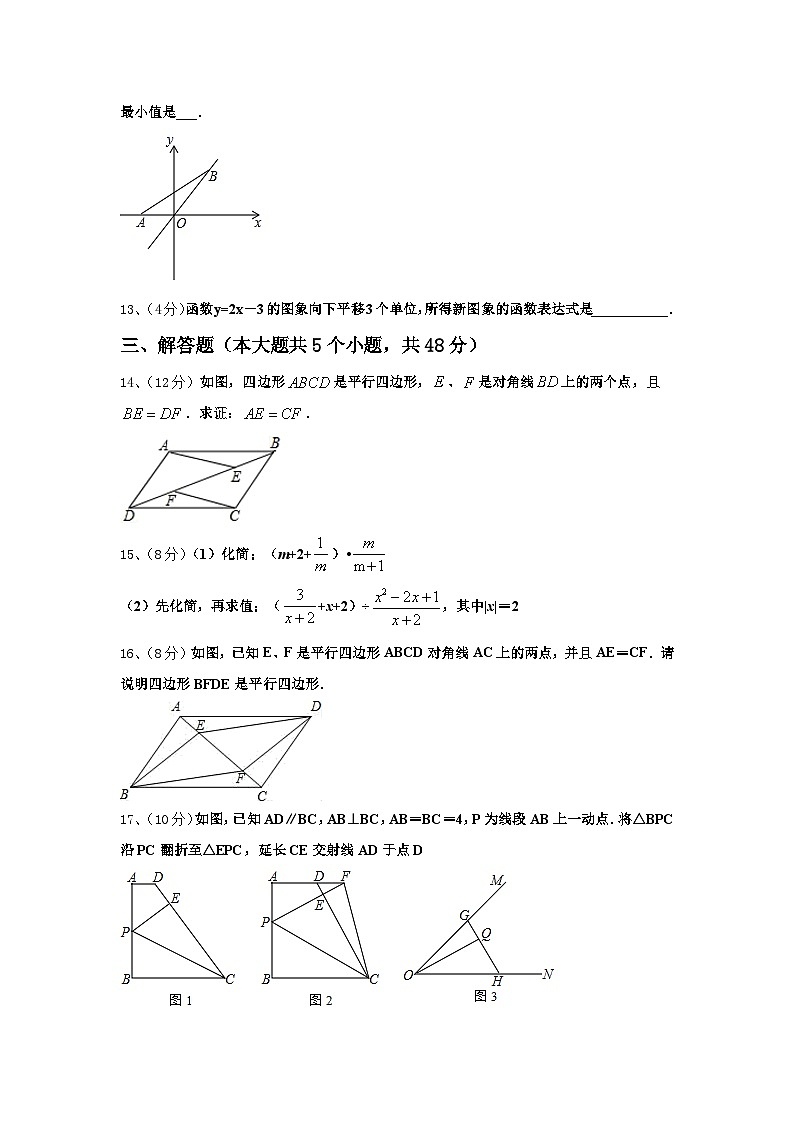
12、（4分）如图，点A的坐标为，点B在直线上运动则线段AB的长度的最小值是___．
13、（4分）函数y=2x－3的图象向下平移3个单位，所得新图象的函数表达式是___________．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，四边形是平行四边形，、是对角线上的两个点，且．求证：．
15、（8分）（1）化简；（m+2+）•
（2）先化简，再求值；（+x+2）÷，其中|x|＝2
16、（8分）如图，已知E、F是平行四边形ABCD对角线AC上的两点，并且AE＝CF．请说明四边形BFDE是平行四边形．
17、（10分）如图，已知AD∥BC，AB⊥BC，AB＝BC＝4，P为线段AB上一动点．将△BPC沿PC翻折至△EPC，延长CE交射线AD于点D

（1）如图1，当P为AB的中点时，求出AD的长
（2）如图2，延长PE交AD于点F，连接CF，求证：∠PCF＝45°
（3）如图3，∠MON＝45°，在∠MON内部有一点Q，且OQ＝8，过点Q作OQ的垂线GH分别交OM、ON于G、H两点．设QG＝x，QH＝y，直接写出y关于x的函数解析式
18、（10分）如图，直线l1经过过点P（1，2），分别交x轴、y轴于点A（2，0），B．
（1）求B点坐标；
（2）点C为x轴负半轴上一点，过点C的直线l2：交线段AB于点D．
①如图1，当点D恰与点P重合时，点Q（t，0）为x轴上一动点，过点Q作QM⊥x轴，分别交直线l1、l2于点M、N．若，MN=2MQ，求t的值；
②如图2，若BC=CD，试判断m，n之间的数量关系并说明理由．

B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，直线与轴、轴分别交于两点，过点作轴与双曲线交于点，过作轴于．若梯形的面积为4，则的值为_____．
A
B
C
D
O
x
y
20、（4分）如图，直线AB的解析式为y=x+4，与y轴交于点A，与x轴交于点B，点P为线段AB上的一个动点，作PE⊥y轴于点E，PF⊥x轴于点F，连接EF，则线段EF的最小值为_____．
21、（4分）等腰三角形的两条中位线分别为3和5，则等腰三角形的周长为_____．
22、（4分）如图，为的中位线，点在上，且为直角，若 ，，则的长为_____．
23、（4分）已知y＝（k﹣1）x+k2﹣1是正比例函数，则k＝_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）己知：，，求下列代数式的值：
（1）；
（2）．
25、（10分）如图所示，已知△ABC的三个顶点的坐标分别为A（﹣1，3），B（﹣6，0），C（﹣1，0）．
（1）请直接写出点A关于原点O对称的点坐标；
（1）将△ABC向右平移6个单位，再向上平移3个单位，得到△A1B1C1，画出△A1B1C1；
（3）将△ABC绕点O逆时针转90°，得到△A1B1 C1，画出△A1B1 C1．
26、（12分）如图，在矩形中，点为上一点，连接、，．
（1）如图1，若，，求的长．
（2）如图2，点是的中点，连接并延长交于，为上一点，连接，且，求证：．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
试题分析：由题意可得，甲的平均数为：（9+8+7+7+9）÷5=8；
方差为：=0.8
乙的平均数为：（10+8+9+7+1）÷5=8；
方差为：=2；
∵0.8＜2，∴选择甲射击运动员，故选A．
考点：方差．
2、D
【解析】
首先根据数轴可以得到a、b的取值范围，然后利用绝对值的定义去掉绝对值符号后化简即可．
【详解】
由数轴上各点的位置可知：a<0∴|a+b|−a=a+b−a=b.
故选D.
此题考查整式的加减，实数与数轴，解题关键在于结合数轴分析a,b的大小.
3、C
【解析】
将一组数据按大小依次排列，把处在最中间位置的一个数据（或最中间两个数据的平均数）叫做这组数据的中位数.
【详解】
根据中位数的概念，可知这组数据的中位数为:21
故答案选：C
本题考查中位数的概念，将一组数据从小到大或从大到小重新排列后，最中间的那个数或者最中间两个数的平均数叫做这组数据中位数，如果中位数的概念掌握不好，不把数据按照要求重新排列，就会出错.
4、C
【解析】
利用二次根式的加减运算及立方根的定义，逐一分析四个选项的正误即可得出结论．
【详解】
解：A、＞3＞，
∴选项A不正确；
B、，
∴选项B不正确；
C、（）2＝2，
∴选项C正确；
D、＝3，
∴选项D不正确．
故选C．
本题考查了立方根、算式平方根以及二次根式的加减，利用排除法逐一分析四个选项的正误是解题的关键．
5、A
【解析】
根据方差的意义可作出判断．方差是用来衡量一组数据波动大小的量，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
【详解】
∵甲、乙两个同学的平均成绩都是112分，方差分别是S甲2=5，S乙2=12，
∴S甲2＜S乙2，
∴成绩比较稳定的是甲；
故选A．
本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
6、C
【解析】
过D作直线EF与平行线垂直，交l1与点E，交l4于点F.再证明，得到 ，故可求的CD的长，进而求出正方形的面积.
【详解】
过D作直线EF与l2垂直，交l1与点E，交l4于点F.

,即
四边形ABCD为正方形




在和中





即正方形的面积为20
故选C.
本题主要考查平行线的性质，关键在于利用三角形全等求正方形的边长.
7、A
【解析】
连结，可说明四边形是平行四边形，即是的中点；由有题意的可得O是BD的中点，即可判定①；运用菱形和平行四边形的性质寻找判定全等三角形的条件，找出与其全等的三角形即可判定②；证出OG是△ABD的中位线，得出OG//AB，OG=AB，得出△GOD∽△ABD，△ABF∽△OGF，由相似三角形的性质和面积关系得出S四边形0DGF=S△ABF.即可判定③；先说明△ABD是等边三角形,则BD=AB,即可判定④．
【详解】
解：如图：连结．
，，
四边形是平行四边形，
是的中点，
∵O是BD的中点
，①正确；
有，，，，，，共个，②错误；
∵OB=OD，AG=DG，
∴OG是△ABD的中位线，
∴OG//AB，OG=AB，
∴△GOD∽△ABD，△ABF∽△OGF，
∵△GOD的面积=△ABD的面积，△ABF的面积=△OGF的面积的4倍，AF:OF=2:1，
∴△AFG的面积=△OGF的面积的2倍，
又∵△GOD的面积=△A0G的面积=△B0G的面积，
.∴；不正确；③错误；
是等边三角形．
，
是菱形，④正确．
故答案为A．
本题考查了菱形的判定与性质、全等三角形的判定与性质、等边三角形的判定与性质、三角形中位线定理、相似三角形的判定与性质等知识；考查知识点较多、难道较大，解题的关键在于对所学知识的灵活应用．
8、D
【解析】
根据分式有意义的条件可得x+3≠0，再解即可．
【详解】
由题意得：x+3≠0，
解得：x≠3，
故选D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、4
【解析】
根据等边三角形的性质和含30°的直角三角形的性质解答即可．
【详解】
∵在△ABC中,∠B=∠C=60°，
∴∠A=60°，
∵DE⊥AB，
∴∠AED=30°，
∵AD=1，
∴AE=2，
∵BC=6，
∴AC=BC=6，
∴CE=AC−AE=6−2=4.
故答案为4.
本题考查了等边三角形的性质，解题的关键是熟练的掌握等边三角形的性质.
10、3
【解析】
根据菱形的对角线互相垂直平分可得AC⊥BD，BD=2OB，菱形的对角线平分一组对角线可得∠ABO=30°，根据直角三角形30°角所对的直角边等于斜边的一半可得AO=AB，再利用勾股定理列式求出OB，即可得解．
【详解】
解：如图所示：
∵菱形ABCD的周长为12，
∴AB=3，AC⊥BD，BD=2OB，
∵∠ABC=60°，
∴∠ABO=∠ABC=30°，
∴AO=AB=×3=，
由勾股定理得，OB===，
∴BD=2OB=3．
故答案为：3．
本题考查了菱形的性质，直角三角形30°角所对的直角边等于斜边的一半的性质，勾股定理，熟记性质是解题的关键，作出图形更形象直观．
11、1
【解析】
【分析】先根据众数的定义求出x=5，再根据中位数的定义进行求解即可得．
【详解】∵数据6，x，3，3，5，1的众数是3和5，
∴x=5，
则这组数据为1、3、3、5、5、6，
∴这组数据的中位数为=1，
故答案为：1．
【点睛】本题主要考查众数和中位数，熟练掌握众数和中位数的定义以及求解方法是解题的关键.
12、
【解析】
当线段AB最短时，直线AB与直线垂直，根据勾股定理求得AB的最短长度．
【详解】
解：当线段AB最短时，直线AB与直线垂直，
过点A作直线l，
因为直线是一、三象限的角平分线，
所以，
所以，
所以，
，即，
所以．
故答案是：．
考查了垂线段最短的性质，一次函数图象上点的坐标特征，勾股定理的应用，熟知垂线段最短是解题的关键．
13、y=2x-6
【解析】
根据“左加右减，上加下减”的原则进行解答即可.
【详解】
解：函数y=2x－3的图像向下平移3个单位，所得新图像的函数表达式是y=2x-6.
故答案为y=2x-6.
本题主要考查一次函数图象的平移，解此题的关键在于熟记“左加右减，上加下减”.
三、解答题（本大题共5个小题，共48分）
14、见解析
【解析】
先根据平行四边形的性质得，，则，再证明得到AE＝CF．
【详解】
证明：∵四边形为平行四边形
∴，
∴
∵
∴
∴
本题考查了平行四边形的性质：平行四边形的对边相等；平行四边形的对角相等；平行四边形的对角线互相平分．
15、（1）m+1；（2）1
【解析】
（1）先对括号里面的式子进行合并，再利用完全平方公式进行计算即可解答.
（2）先合并括号里面的，再把除法变成乘法，约分合并，最后把|x|＝2，代入即可.
【详解】
解：（1）原式＝＝m+1；
（2）原式＝ ，
由|x|＝2，得到x＝2或﹣2（舍去），
当x＝2时，原式＝1．
此题考查分式的化简求值，解题关键在于掌握运算法则.
16、证明见解析.
【解析】
连接BD，利用对角线互相平分来证明即可．
【详解】
证明：连接BD，交AC于点O．
∵四边形ABCD是平行四边形
∴OA＝OC OB＝OD(平行四边形的对角线互相平分)
又∵AE＝CF
∴OA﹣AE＝OC﹣CF，即OE＝OF
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)
本题考查平行四边形的性质和判定，解题的关键是熟练掌握平行四边形的判定和性质，属于中考常考题型．
17、（1）1；（2）见解析；（3）
【解析】
(1)如图1.根据平行线的性质得到∠A=∠B=90°，由折叠的性质得到∠CEP=∠B=90°，PB=PE，∠BPC=∠EPC,根据全等三角形的性质得到∠APD=∠EPD,推出 于是得到结论；
(2)如图2.过C作CG⊥AF交AF的延长线于G,推出四边形ABCG是矩形，得到矩形ABCG是正方形，求得CG=CB，根据折叠的性质得到∠CEP=∠B=90°，BC=CE，∠BCP=∠ECP, 根据全等三角形的性质即可得到结论:
(3)如图3，将△OQG沿OM翻折至△OPG,将△OQH沿ON翻折至△ORH,延长PG, RH交于S,推出四边形PORS是正方形，根据勾股定理即可得到结论．
【详解】
解：（1）如图1，连结，
∵AD//BC. AB⊥BC,
∴∠A=∠B=90°
∵将△BPC沿PC翻折至△EPC,
∴∠CEP=∠B=90°，PB=PE，∠BPC=∠EPC,
∴∠DEP=90°
∵当P为AB的中点，
∴AP=BP
∴PA=PE
∵PD=PD
∴，
∴
作于，设，则，
由勾股定理得，
解得，
∴
图1
（2）如图2，作交延长线于，易证四边形为正方形
∵∠A=∠B=∠G=90°,
∴四边形ABCG是矩形,
∵AB=BC,
∴矩形ABCG是正方形,
∴CG=CB.
∵将△BPC沿PC翻折至△EPC,
∴∠ FED=90°，CG=CE,
又∵CF=CF
∴，
∴∠ECF=∠GCF,
∴∠BCP+∠GCF=∠PCE+∠FCE=45°
∴∠PCF=45°;
图2
(3)如图3.将△OQG沿OM翻折至OOPG.将△OQH沿ON翻折至△ORH.延长PG, RH交于S,则∠POG=∠QOG.∠ROH=∠QOH, OP=OQ=OR=8,PG=QG=x,QH=RH=y,
∴ ∠POR=2∠MON=90",
∵GH⊥OQ.
∴∠OQG=∠OQH=90° .
∴∠P=∠R=90° ,
∴四边形PORS是正方形。
∴PS=RS=8,∠S=90°，
∴.GS=8-x,HS=8-y.
∴ .
∴
∴
图3
本题考查了折叠的性质，全等三角形的判定和性质，正方形的判定和性质，正确的作出辅助线是解题的关键．
18、 (1) ；（2）①，；②
【解析】
【分析】（1）用待定系数法求解；（2）点Q的位置有两种情况：当点Q在点A左侧，点P的右侧时；当点Q在点P的右侧时，.都有，再根据MN=2MQ，可求t的值；（3）由BC=CD，证△BCO≌△CDE，设C（a，0），D（4+a，-a），并代入解析式，通过解方程组可得.
【详解】解：(1)设直线l1的解析式为y=kx+b，
直线经过点P（2，2），A（4，0），
即, 解得，
直线l1的解析式为y=-x+4；
（2）①∵直线l2过点P（2，2）且,
即直线l2：，
点Q（t，0），M（t，4-t），N（t，），
1. 当点Q在点A左侧，点P的右侧时，
，，
即，解得；
⒉ 当点Q在点A右侧时
，MQ=t-4,
即，解得t=10，
②过点D作DE⊥AC于E ,
∵BC=CD，BO=OA，
∠DBC=∠1+∠ABO=∠BDC=∠2+∠DAE,
∴∠1=∠2，
∴△BCO≌△CDE，
∴OC=ED，BO=CE，
设C（a，0），D（4+a，-a），
则，
解得，
即
【点睛】本题考核知识点：一次函数综合应用. 本题先用待定系数法求解析式，比较容易；后面要根据数形结合，结合线段的和差关系，情况讨论，比较综合；最后一小题要先证明三角形全等，得到线段的关系，再根据这个关系列出方程组，化简得到答案，这也比较难.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、-2
【解析】由题意可知，OB=2，OA=2，所以三角形OAB的面积等于2，四边形BCDO的面积等于4-2=2, 点C在双曲线上，所以k=-2
20、
【解析】
在一次函数y=x+4中，分别令x=0， y=0，解相应方程，可求得A、B两点的坐标，由矩形的性质可知EF=OP，可知当OP最小时，则EF有最小值，由垂线段最短可知当OP⊥AB时，满足条件，根据直角三角形面积的不同表示方法可求得OP的长，即可求得EF的最小值．
【详解】
解：∵一次函数y=x+4中，令x=0，则y=4，令y=0，则x=-3，
∴A（0，4），B（-3，0），
∵PE⊥y轴于点E，PF⊥x轴于点F，
∴四边形PEOF是矩形，且EF=OP，
∵O为定点，P在线段上AB运动，
∴当OP⊥AB时，OP取得最小值，此时EF最小，
∵A（0，4），点B坐标为（-3，0），
∴OA=4，O B=3，
由勾股定理得：AB==5，
∵AB·OP=AO·BO=2S△OAB，
∴OP=，
故答案为：．
本题考查了一次函数图象上点的坐标特点，勾股定理、矩形的判定与性质、最值问题等，熟练掌握相关知识、确定出OP的最小值是解题的关键．
21、22或1．
【解析】
因为三角形中位线的长度是相对应边长的一半，所以此三角形有一条边为6，一条为10；那么就有两种情况，或腰为10，或腰为6，再分别去求三角形的周长．
【详解】
解：∵等腰三角形的两条中位线长分别为3和5，
∴等腰三角形的两边长为6，10，
当腰为6时，则三边长为6，6，10；周长为22；
当腰为10时，则三边长为6，10，10；周长为1；
故答案为：22或1．
此题涉及到三角形中位线与其三边的关系，解答此题时要注意分类讨论，不要漏解．
22、1cm．
【解析】
根据三角形中位线定理求出DE，根据直角三角形的性质求出EF，结合图形计算即可．
【详解】
∵DE为△ABC的中位线，
∴DE＝BC＝4（cm），
∵∠AFC为直角，E为AC的中点，
∴FE＝AC＝3（cm），
∴DF＝DE﹣FE＝1（cm），
故答案为1cm．
本题考查的是三角形中位线定理，直角三角形的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
23、-1
【解析】
【分析】根据正比例函数的定义可知k-1≠0，常数项k2-1=0，由此即可求得答案.
【详解】∵y=（k-1）x+k2-1是正比例函数，
∴k-1≠0，k2-1=0，
解得k≠1，k=±1，
∴k=-1，
故答案为-1．
【点睛】本题考查了正比例函数的定义，熟知正比例函数y=kx中一次项系数中不为0，常数项等于0是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、 (1);(2)
【解析】
（1）首先将代数式进行通分，然后根据已知式子，即可得解；
（2）首先根据完全平方差公式，将代数式展开，然后将已知式子转换形式，代入即可得解.
【详解】
∵，，
∴，
（1）
（2）
此题主要考查二次根式的运算，熟练掌握，即可解题.
25、（1）（1，-3）；（1）详见解析；（3）详见解析
【解析】
（1）根据关于原点对称的点的特征即可；
（1）根据平移方向画出图形即可；
（3）根据旋转角度及旋转方向画出图形即可．
【详解】
（1）点A关于原点对称的点坐标为（1，-3）
（1）如下图所示，
（3）如下图所示，
本题考查了关于原点对称的点的特征及平移画图，旋转画图问题，解题的关键是明确平移方向或旋转方向．
26、（1）；（2）见解析
【解析】
（1）利用等腰直角三角形的性质及勾股定理求AB和AE的长，然后根据矩形的性质求得CD和ED的长，从而利用勾股定理求解；
（2）延长交的延长线于，利用AAS定理证得，得到，，然后求得，从而使问题得解．
【详解】
解：（1）∵矩形，∴
又∵
∴
设，在中，
即
解得：，（舍）
∴
∵矩形∴，
∴
在中，，
∴；
（2）如答图，延长交的延长线于
∵，∴
又∵为的中点，∴
在和中
∴
∴，
∵，
∴
∴
∴
∴
本题考查矩形的性质，勾股定理解直角三角形，全等三角形的判定和性质，等腰三角形的判定和性质，有一定的综合性，掌握相关性质定理正确推理论证是解题关键．
题号
一
二
三
四
五
总分
得分