广西柳州市2024-2025学年九上数学开学调研模拟试题【含答案】

这是一份广西柳州市2024-2025学年九上数学开学调研模拟试题【含答案】，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）一元二次方程的根是（ ）
A．B．C．，D．，
2、（4分）已知P1（﹣1，y1），P2（2，y2）是一次函数y＝﹣x+1图象上的两个点，则y1，y2的大小关系是（ ）
A．y1＝y2B．y1＜y2C．y1＞y2D．不能确定
3、（4分）下列各组线段中，能够组成直角三角形的一组是（ ）
A．1，2，3B．2，3，4C．4，5，6D．1，，2
4、（4分）已知，则的大小关系是（ ）
A．B．C．D．
5、（4分）使分式有意义的的取值范围是（ ）
A．B．C．D．
6、（4分）下列事件中，属于不确定事件的是（ ）
A．科学实验，前100次实验都失败了，第101次实验会成功
B．投掷一枚骰子，朝上面出现的点数是7点
C．太阳从西边升起来了
D．用长度分别是3cm，4cm，5cm的细木条首尾顺次相连可组成一个直角三角形
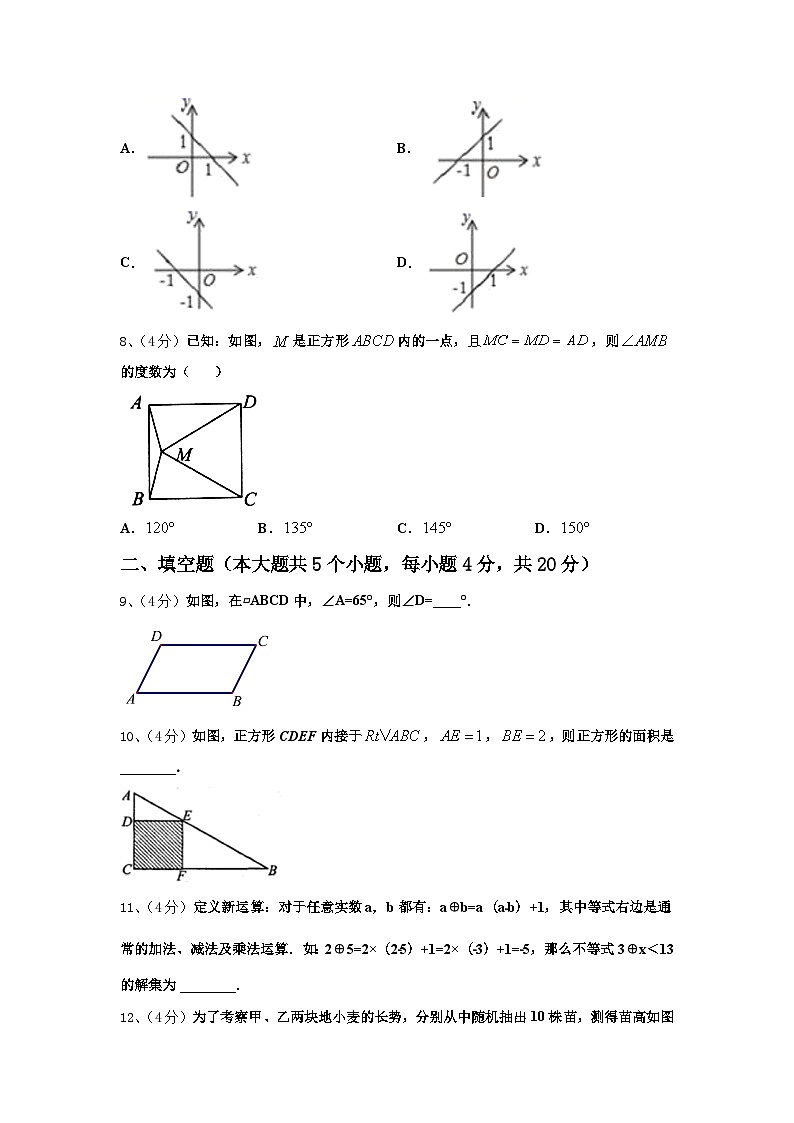
7、（4分）函数y=x-1的图象是（ ）
A．B．
C．D．
8、（4分）已知：如图，是正方形内的一点，且，则的度数为（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，在▱ABCD中，∠A=65°，则∠D=____°．
10、（4分）如图，正方形CDEF内接于，，，则正方形的面积是________.
11、（4分）定义新运算：对于任意实数a，b都有：a⊕b=a（a﹣b）+1，其中等式右边是通常的加法、减法及乘法运算．如：2⊕5=2×（2﹣5）+1=2×（﹣3）+1=﹣5，那么不等式3⊕x＜13的解集为 ________.
12、（4分）为了考察甲、乙两块地小麦的长势，分别从中随机抽出10株苗，测得苗高如图所示．若和 分别表示甲、乙两块地苗高数据的方差，则________．(填“>”、“<”或“=”)．
13、（4分）把直线y＝﹣x﹣1沿着y轴向上平移2个单位，所得直线的函数解析式为_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）数学活动课上，老师提出了一个问题：如图1，A、B两点被池塘隔开，在AB外选一点，连接AC和BC，怎样测出A、B两点的距离？
（活动探究）学生以小组展开讨论，总结出以下方法：
⑴如图2，选取点C，使AC=BC=a，∠C=60°；
⑵如图3，选取点C，使AC=BC=b，∠C=90°；
⑶如图4，选取点C，连接AC，BC，然后取AC、BC的中点D、E，量得DE=c…
（活动总结）
（1）请根据上述三种方法，依次写出A、B两点的距离．（用含字母的代数式表示）并写出方法⑶所根据的定理．AB=________，AB=________，AB=________．定理：________．
（2）请你再设计一种测量方法，（图5）画出图形，简要说明过程及结果即可．
15、（8分）某种型号油电混合动力汽车，从A地到B地燃油行驶需纯燃油费用76元，从A地到B地用电行驶需纯用电费用26元，已知每行驶1千米，纯燃油费用比纯用电费用多0.5元．
(1)求每行驶1千米纯用电的费用；
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元，则至少需用电行驶多少千米？
16、（8分）甲、乙两名射击选示在10次射击训练中的成绩统计图（部分）如图所示：
根据以上信息，请解答下面的问题；
（1）补全甲选手10次成绩频数分布图．
（2）a＝ ，b＝ ，c＝ ．
（3）教练根据两名选手手的10次成绩，决定选甲选手参加射击比赛，教练的理由是什么？（至少从两个不同角度说明理由）．
17、（10分）如图，在的方格中，的顶点均在格点上．试按要求画出线段（，均为格点），各画出一条即可．

18、（10分）已知：如图在菱形ABCD中，AB=4，∠DAB=30°，点E是AD的中点，点M是的一个动点（不与点A重合），连接ME并廷长交CD的延长线于点N连接MD，AN．
（1）求证：四边形AMDN是平行四边形；（2）当AM为何值时，四边形AMDN是矩形并说明理由．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）若关于x的方程-2=会产生增根，则k的值为________
20、（4分）中美贸易战以来，强国需更多的中国制造，中芯国际扛起中国芯片大旗，目前我国能制造芯片的最小工艺水平已经达到7纳米，居世界前列，已知1纳米=0.000000001米，用料学记数法将7纳米表示为______米.
21、（4分）如图，线段两个点的坐标分别为，，以原点为位似中心，将线段缩小得到线段，若点的坐标为，则点的坐标为______．
22、（4分）已知一次函数y=（-1-a2）x+1的图象过点（x1，2），（x2-1），则x1与x2的大小关系为______．
23、（4分）已知是整数，则正整数n的最小值为___
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．
（1）求证：四边形AODE是矩形；
（2）若AB＝2，AC＝2，求四边形AODE的周长．
25、（10分）如图，方格纸中每个小方格都是边长为1的正方形，已知学校的坐标为A(2，2)．
(1)请在图中建立适当的直角坐标系，并写出图书馆的坐标；
(2)若体育馆的坐标为C(－2，3)，请在坐标系中标出体育馆的位置，并顺次连接学校、图书馆、体育馆，得到△ABC，求△ABC的面积．
26、（12分）学校准备购进一批节能灯，已知1只A型节能灯和3只B型节能灯共需26元；3只A型节能灯和2只B型节能灯共需29元。
（1）求1只A型节能灯和1只B型节能灯的售价各是多少元？
（2）学校准备购进这两种型号的节能灯共80只，并且A型节能灯的数量不多于B型节能灯的3倍，问如何购买最省钱，说明理由。
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
利用因式分解法解方程．
【详解】
∵x(x+3)=0，
∴x=0，或x+3=0，
解得x=0或x=−3.
故选D.
本题主要考查解一元二次方程-因式分解法，熟悉掌握是关键.
2、C
【解析】
根据P1（-3，y1），P1（1，y1）是一次函数y=-x-1的图象上的两个点，根据一次函数k=-1<0可得：y随x的增大而减小判断出y1，y1的大小．
【详解】
∵P1（-3，y1），P1（1，y1）是一次函数y=-x-1的图象上的两个点，且-3＜1，
∴y1＞y1．
故选C．
考查了一次函数的性质，解题关键是熟记一次函数的性质：k>0时，图象从左到右上升，y随x的增大而增大；k<0时，图象从左到右下降，y随x的增大而减小．
3、D
【解析】
根据勾股定理的逆定理判断即可．
【详解】
解：1+2＝3，A不能构成三角形；
22+32≠42，B不能构成直角三角形；
42+52≠62，C不能构成直角三角形；
12+（）2＝22，D能构成直角三角形；
故选：D．
本题考查了能构成直角三角形的三边关系，解题的关键是掌握勾股定理.
4、B
【解析】
先根据幂的运算法则进行计算，再比较实数的大小即可.
【详解】
，
，
，
.
故选：.
此题主要考查幂的运算，准确进行计算是解题的关键.
5、A
【解析】
根据分式有意义的条件进行求解即可.
【详解】
由题意得，x+2≠0，
解得：x≠-2，
故选A.
本题考查了分式有意义的条件，熟练掌握“分母不为0时，分式有意义”是解题的关键.
6、A
【解析】
根据事件发生的可能性大小判断相应事件的类型即可．
【详解】
解：A、是随机事件，故A符合题意；
B、是不可能事件，故B不符合题意；
C、是不可能事件，故C不符合题意；
D、是必然事件，故D不符合题意；
故选A．
本题考查了随机事件，解决本题需要正确理解必然事件、不可能事件、随机事件的
概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不
发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
7、D
【解析】
∵一次函数解析式为y=x-1，
∴令x=0，y=-1．
令y=0，x=1，
即该直线经过点（0，-1）和（1，0）．
故选D．
考点：一次函数的图象．
8、D
【解析】
利用等边三角形和正方形的性质求得，然后利用等腰三角形的性质求得的度数，从而求得的度数，利用三角形的内角和求得的度数．
【详解】
解：，
是等边三角形，
，
，
，
，
，
同理可得，
，
故选：．
本题考查了正方形的性质及等边三角形的性质，解题的关键是根据等腰三角形的性质求得有关角的度数，难度不大．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、115
【解析】
根据平行四边形的对边平行即可求解.
【详解】
依题意知AB∥CD
∴∠D=180°-∠A=115°.
此题主要考查平行四边形的性质，解题的关键是熟知平行四边形的对边平行.
10、0.8
【解析】
根据题意分析可得△ADE∽△EFB，进而可得2DE=BF，2AD=EF=DE，由勾股定理得，DE2+AD2=AE2，可解得DE，正方形的面积等于DE的平方问题得解．
【详解】
∵根据题意,易得△ADE∽△EFB，
∴BE:AE=BF:DE=EF:AD=2:1，
∴2DE=BF，2AD=EF=DE，
由勾股定理得,DE+AD=AE，
解得：DE=EF=，
故正方形的面积是 =，
故答案为：0.8
本题考查相似三角形，熟练掌握相似三角形的判定及基本性质是解题关键.
11、x＞﹣1
【解析】
解：3⊕x＜13，
3（3-x）+1＜13，
解得：x＞-1．
故答案为：x＞﹣1
本题考查一元一次不等式的应用，正确理解题意进行计算是本题的解题关键．
12、<
【解析】
方差用来计算每一个变量（观察值）与总体均数之间的差异，所以从图像看苗高的波动幅度，可以大致估计甲、乙两块地苗高数据的方差.
【详解】
解：由图可知，甲、乙两块地的苗高皆在12cm上下波动，但乙的波动幅度比甲大，
∴ 则
故答案为：<
本题考查了方差，方差反映了数据的波动程度，方差越大，数据的波动越大，正确理解方差的含义是解题的关键.
13、y＝﹣x+1
【解析】
根据“上加下减”的平移规律可直接求得答案．
【详解】
解：把直线y＝﹣x﹣1沿着y轴向上平移2个单位，所得直线的函数解析式为y＝﹣x﹣1+2，即y＝﹣x+1．
故答案为：y＝﹣x+1．
本题考查一次函数图象与几何变换，掌握平移的规律是解题的关键，即“左加右减，上加下减”．
三、解答题（本大题共5个小题，共48分）
14、见解析
【解析】
试题分析：（1）分别利用等边三角形的判定方法以及直角三角形的性质和三角形中位线定理得出答案；
（2）直接利用利用勾股定理得出答案．
解：（1）∵AC=BC=a，∠C=60°，
∴△ABC是等边三角形，
∴AB=a；
∵AC=BC=b，∠C=90°，
∴AB=b，
∵取AC、BC的中点D、E，
∴DE∥AB，DE=AB，
量得DE=c，则AB=2c（三角形中位线定理）；
故答案为a，b，2c，三角形中位线定理；
（2）方法不唯一，如：图5，选取点C，
使∠CAB=90°，AC=b，BC=a，
则AB=．
【点评】此题主要考查了应用设计与作图，正确应用勾股定理是解题关键．
15、（1）每行驶1千米纯用电的费用为0.26元．（2）至少需用电行驶74千米．
【解析】
（1）根据某种型号油电混合动力汽车，从A地到B地燃油行驶纯燃油费用76元，从A地到B地用电行驶纯电费用26元，已知每行驶1千米，纯燃油费用比纯用电费用多0.5元，可以列出相应的分式方程，然后解分式方程即可解答本题；
（2）根据（1）中用电每千米的费用和本问中的信息可以列出相应的不等式，解不等式即可解答本题．
【详解】
（1）设每行驶1千米纯用电的费用为x元，根据题意得：
=
解得：x=0.26
经检验，x=0.26是原分式方程的解，
答：每行驶1千米纯用电的费用为0.26元；
（2）从A地到B地油电混合行驶，用电行驶y千米，得：
0.26y+（﹣y）×（0.26+0.50）≤39
解得：y≥74，即至少用电行驶74千米．
16、（1）4；（2）8、1.2、7.5；（3）从平均数看，甲成绩优于乙的成绩；从方差看，甲的方差小，说明甲的成绩稳定．
【解析】
（1）根据甲的成绩频数分布图及题意列出10﹣（1+2+2+1），计算即可得到答案；
（2）根据平均数公式、中位数的求法和方差公式计算得到答案；
（3）从平均数和方差进行分析即可得到答案.
【详解】
解：（1）甲选手命中8环的次数为10﹣（1+2+2+1）＝4，
补全图形如下：
（2）a＝＝8（环），
c＝×[（6﹣8）2+2×（7﹣8）2+4×（8﹣8）2+2×（9﹣8）2+（10﹣8）2]＝1.2，
b＝＝7.5，
故答案为：8、1.2、7.5；
（3）从平均数看，甲成绩优于乙的成绩；从方差看，甲的方差小，说明甲的成绩稳定．
本题考查频数分布直方图、平均数、中位数和方差，解题的关键是读懂频数分布直方图，掌握平均数、中位数和方差的求法.
17、见解析
【解析】
图1，从图中可得到AC边的中点在格点上设为E，过E作AB的平行线即可在格点上找到F；图2，EC=，EF=，FC=，借助勾股定理确定F点．
【详解】
解：如图：
本题考查三角形作图；在格点中利用勾股定理，三角形的性质作平行、垂直是解题的关键．
18、（1）见解析；（1），四边形AMDN是矩形，见解析.
【解析】
（1）根据菱形的性质可得ND∥AM，再根据两直线平行，内错角相等可得∠NDE=∠MAE，∠DNE=∠AME，根据中点的定义求出DE=AE，然后利用“角角边”证明△NDE和△MAE全等，根据全等三角形对应边相等得到ND=MA，然后利用一组对边平行且相等的四边形是平行四边形证明；
（1）根据矩形的性质得到DM⊥AB，结合∠DAB=30°，由直角三角形30°角所对的直角边等于斜边的一半解答．
【详解】
（1）证明：∵四边形ABCD是菱形，
∴ND∥AM．
∴∠NDE=∠MAE，∠DNE=∠AME．
∵点E是AD中点，
∴DE=AE．
在△NDE和△MAE中，
，
∴△NDE≌△MAE（AAS）．
∴ND=MA．
∴四边形AMDN是平行四边形；
（1）解：当AM=1时，四边形AMDN是矩形．理由如下：
∵四边形ABCD是菱形，
∴AD=AB=1，
∵平行四边形AMDN是矩形，
∴∠AMD=90°．
∵∠DAB=30°，
∴MD=AD=AB=1．
在直角△AMD中，．
本题考查了菱形的性质，平行四边形的判定，全等三角形的判定与性质，矩形的性质，熟记各性质并求出三角形全等是解题的关键，也是本题的突破口．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
根据方程有增根可得x=3，把-2=去分母后，再把x=3代入即可求出k的值.
【详解】
∵关于x的方程-2=会产生增根，
∴x-3=0，
∴x=3.
把-2=的两边都乘以x-3得，
x-2(x-3)=-k，
把x=3代入，得
3=-k，
∴k=-3.
故答案为：-3.
本题考查的是分式方程的增根，在分式方程变形的过程中，产生的不适合原方程的根叫做分式方程的增根.增根使最简公分母等于0，不适合原分式方程，但是适合去分母后的整式方程．
20、
【解析】
绝对值小于1的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】
1纳米米.
故7纳米
故答案为:
本题考查用科学记数法表示较小的数,一般形式为,其中,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
21、
【解析】
利用点B和点D的坐标之间的关系得到线段AB缩小2.5倍得到线段CD，然后确定C点坐标．
【详解】
解：∵将线段AB缩小得到线段CD，点B（5，0）的对应点D的坐标为（2.0），
∴线段AB缩小2.5倍得到线段CD，
∴点C的坐标为（1，2）．
本题考查了位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k．
22、x1＜x1
【解析】
由k=-1-a1,可得y随着x的增大而减小，由于1＞-1， 所以x1＜x1.
【详解】
∵y=（-1-a1）x+1，k=-1-a1＜0，
∴y随着x的增大而减小，
∵1＞-1，
∴x1＜x1．
故答案为：x1＜x1
本题考查的是一次函数，熟练掌握一次函数的性质是解题的关键.
23、1
【解析】
因为是整数，且，则1n是完全平方数，满足条件的最小正整数n为1．
【详解】
∵，且是整数，
∴是整数，即1n是完全平方数；
∴n的最小正整数值为1．
故答案为：1．
主要考查了二次根式的定义，关键是根据乘除法法则和二次根式有意义的条件．二次根式有意义的条件是被开方数是非负数进行解答．
二、解答题（本大题共3个小题，共30分）
24、（1）见解析；（2）四边形AODE的周长为2+2．
【解析】
（1）根据题意可判断出四边形AODE是平行四边形，再由菱形的性质可得出AC⊥BD，即∠AOD=90°，继而可判断出四边形AODE是矩形；
（2）由菱形的性质和勾股定理求出OB，得出OD，由矩形的性质即可得出答案．
【详解】
（1）证明：∵DE∥AC，AE∥BD，
∴四边形AODE是平行四边形，
∵四边形ABCD是菱形，
∴AC⊥BD，
∴∠AOD＝∠AOD＝90°，
∴四边形AODE是矩形；
（2）∵四边形ABCD为菱形，
∴AO＝AC＝1，OD＝OB，
∵∠AOB＝90°，
∴OB＝，
∴OD＝，
∵四边形AODE是矩形，
∴DE＝OA＝1，AE＝OD＝，
∴四边形AODE的周长＝2+2．
本题考查了菱形的性质、矩形的判定与性质、勾股定理、平行四边形的判定；熟练掌握矩形的判定与性质和菱形的性质是解决问题的关键．
25、（1）直角坐标系见解析；图书馆的坐标为B(－2，－2)；（2）△ABC的面积为10.
【解析】
【分析】(1) A(2，2)推出原点，建立平面直角坐标系；（2）直接描出C(－2，3)，由点的坐标得到BC边长为5，BC边上的高为4，再计算面积.
【详解】解：(1)直角坐标系如图所示．
图书馆的坐标为B(－2，－2)．
(2)体育馆的位置C如图所示．观察可得△ABC中BC边长为5，BC边上的高为4，所以△ABC的面积为×5×4＝10.
【点睛】本题考核知识点：平面直角坐标系. 解题关键点：理解坐标的意义，利用坐标求出线段长度.
26、（1）1只A型节能灯的售价为5元，1只B型节能灯的售价为7元；（2）购买60只A型节能灯，20只B型节能灯最省钱,理由见解析
【解析】
（1）设一只A型节能灯的售价是x元，一只B型节能灯的售价y元，根据题意列出方程组，求出方程组的解即可；
（2）设A型节能灯买了a只，则B型节能灯买了（80-a）只，共花费w元，根据题意列出不等式组，求出不等式组的解集即可.
【详解】
解（1）设1只A型节能灯的售价为x元，1只B型节能灯的售价为y元
由题意得：
解得：
答：1只A型节能灯的售价为5元，1只B型节能灯的售价为7元
（2）设购买A型节能灯a个，则购买B型节能灯（80-a）个，总费用为w元
由题意得：a≤3（80-a）
解得a≤60
又∵w=5a+7（80-a）=-2a+560
∴w随a的增大而减小
∴当a取最大值60时，w有最小值
w=-2×60+560=440
即购买60只A型节能灯，20只B型节能灯最省钱
本题考查了解二元一次方程组和一元一次不等式组的应用，能根据题意列出方程组或不等式组是解此题的关键.
题号
一
二
三
四
五
总分
得分
选手
A平均数
中位数
众数
方差
甲
a
8
8
c
乙
7.5
b
6和9
2.65