初中数学湘教版（2024）八年级下册2.5.1矩形的性质习题课件ppt

这是一份初中数学湘教版（2024）八年级下册2.5.1矩形的性质习题课件ppt，共18页。PPT课件主要包含了名师点金等内容，欢迎下载使用。

矩形判定的技巧：证明四边形是矩形，已知对角线相等时，只需再证明四边形是平行四边形；已知四边形是平行四边形时，只需再证明对角线相等或有一个角是直角.如果已知四边形的两个角是直角，此时应选择“有三个角是直角的四边形是矩形”证明.
1.如图，在▱ABCD中，AC＝8，BD＝12，点E，F在对角线BD上，点E从点B出发以每秒1个单位长度的速度向点D运动，同时点F从点D出发以相同速度向点B运动，到端点时运动停止，运动时间为t秒.(1)求证：四边形AECF为平行四边形.
应用1　矩形的性质和判定在平行四边形中的应用
(2)当t为何值时，四边形AECF为矩形？
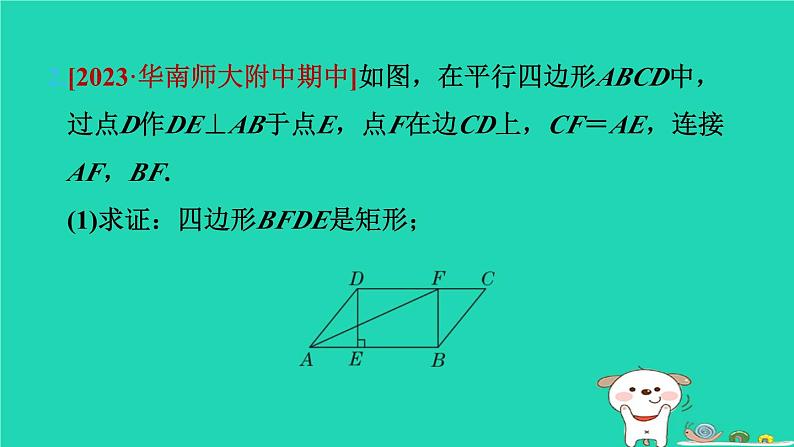
2.[2023·华南师大附中期中]如图，在平行四边形ABCD中，过点D作DE⊥AB于点E，点F在边CD上，CF＝AE，连接AF，BF.(1)求证：四边形BFDE是矩形；
【证明】∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∵CF＝AE，∴AB－AE＝CD－CF，∴BE＝DF.∵BE∥DF，∴四边形BFDE是平行四边形.∵DE⊥AB，∴∠DEB＝90°，∴四边形BFDE是矩形.
(2)若∠DAB＝60°，AF是∠DAB的平分线，AD＝6，求▱ABCD的面积.
应用2　矩形的性质和判定在四边形中的应用3.[2023·新疆]如图，AD和BC相交于点O，∠ABO＝∠DCO＝90°，OB＝OC，点E，F分别是AO，DO的中点.(1)求证：OE＝OF；
(2)当∠A＝30°时，求证：四边形BECF是矩形.
4.[2022·云南]如图，在平行四边形ABCD中，连接BD，E为线段AD的中点，延长BE与CD的延长线交于点F，连接AF，∠BDF＝90°.(1)求证：四边形ABDF是矩形；
∴△BEA≌△FED(ASA).∴EF＝EB.又∵AE＝DE，∴四边形ABDF是平行四边形.又∵∠BDF＝90°，∴四边形ABDF是矩形.
(2)若AD＝5，DF＝3，求四边形ABCF的面积S.