北京市十一学校顺义学校杨镇一中2024-2025学年高二上学期10月月考数学试题(无答案)

这是一份北京市十一学校顺义学校杨镇一中2024-2025学年高二上学期10月月考数学试题(无答案)，共5页。试卷主要包含了解答题等内容，欢迎下载使用。
本试卷共4页，满分150分.考试时长120分钟.
考生务必将答案答在答题卡上，在试卷上作答无效.
第一部分（选择题 共40分）
一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.
1.已知集合，，那么集合等于（ ）
A.B.C.D.
2.某校为了解学生关于校本课程的选课意向，计划从高一、高二这两个年级共500名学生中，采用分层抽样的方法抽取50人进行调查.已知高一年级共有300名学生，那么应抽取高一年级学生的人数为（ ）
A.10B.20C.30D.40
3.不等式的解集为（ ）
A.B.
C.D.
4.在中，，，，则（ ）
A.B.C.D.
5.（ ）
A.B.C.D.
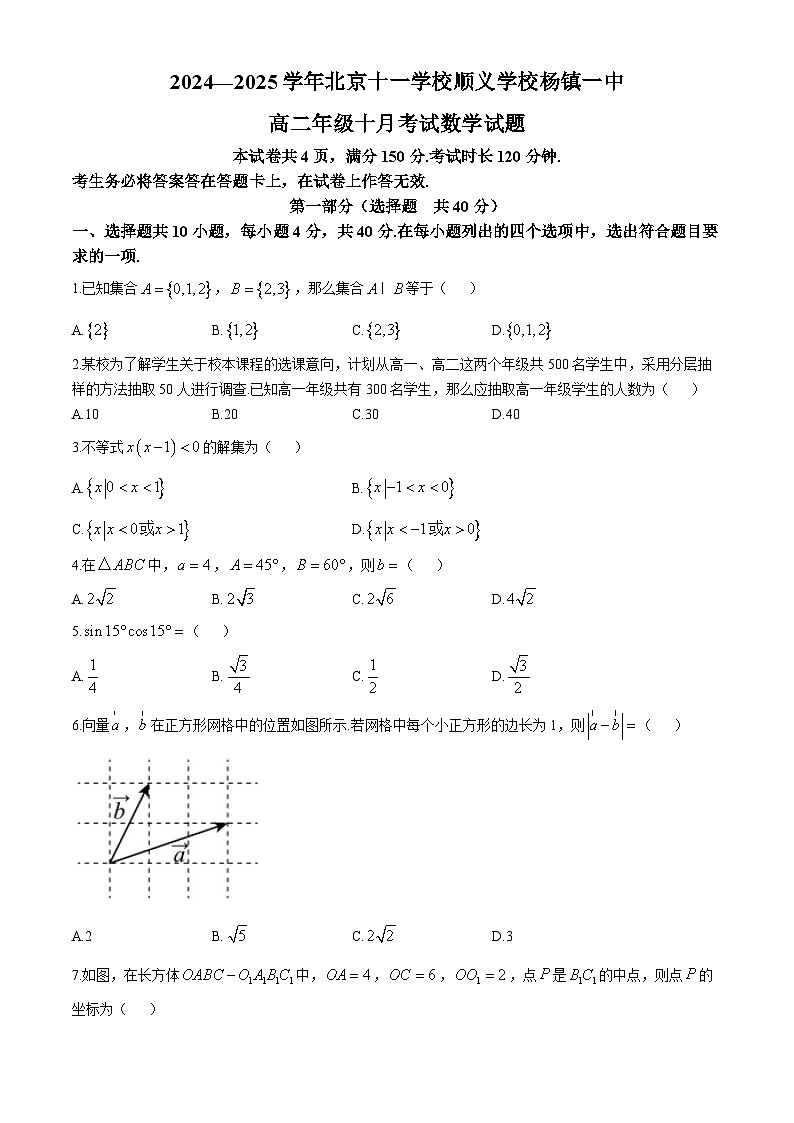
6.向量，在正方形网格中的位置如图所示.若网格中每个小正方形的边长为1，则（ ）
A.2B.C.D.3
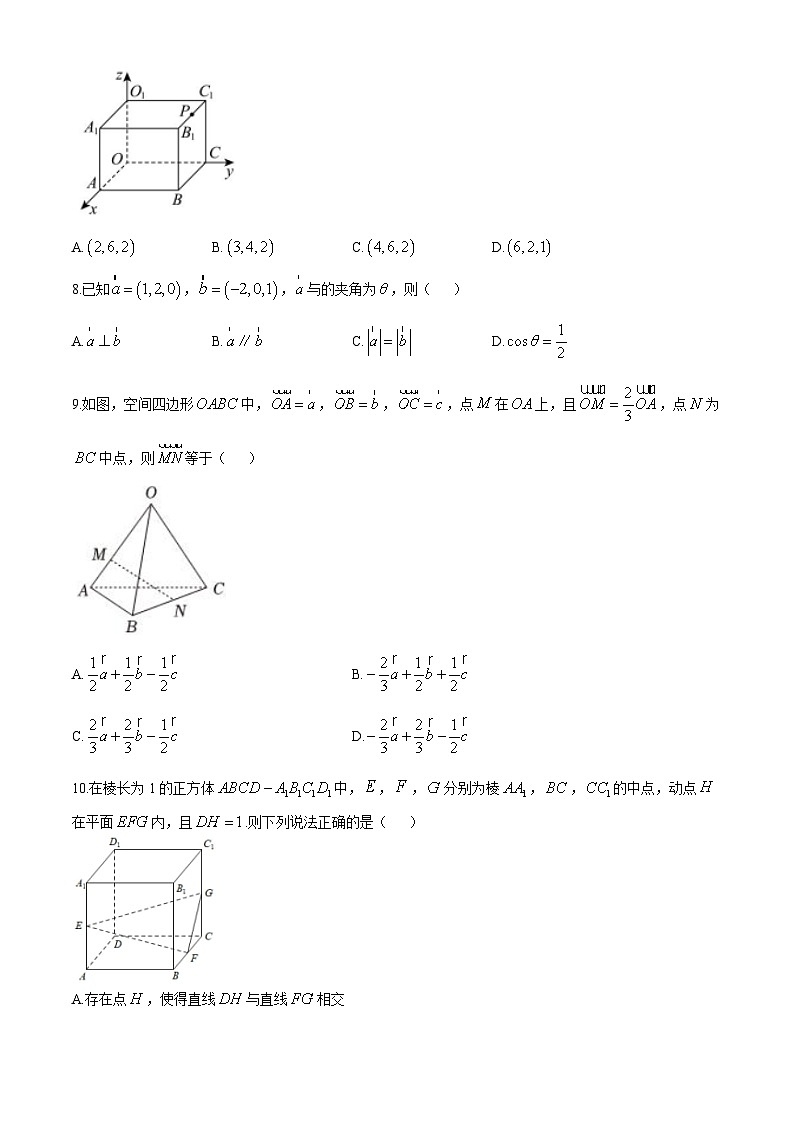
7.如图，在长方体中，，，，点是的中点，则点的坐标为（ ）
A.B.C.D.
8.已知，，与的夹角为，则（ ）
A.B.C.D.
9.如图，空间四边形中，，，，点在上，且，点为中点，则等于（ ）
A.B.
C.D.
10.在棱长为1的正方体中，，，分别为棱，，的中点，动点在平面内，且.则下列说法正确的是（ ）
A.存在点，使得直线与直线相交
B.存在点，使得直线平面
C.直线与平面所成角的大小为
D.平面被正方体所截得的截面面积为
第二部分（非选择题 共110分）
二、填空题共5小题，每小题5分，共25分
11.已知向量，.若，则实数______.
12.______.
13.已知中，，，，那么______.
14.如图，在正三棱柱中，，，为的中点，则异面直线与所成角的余弦值为______.
15.如图，在多面体中，平面，四边形是正方形，且，，，分别是线段，的中点，是线段上的一个动点（含端点，），则下列说法正确的是______
（1）存在点，使得；
（2）存在点，使得异面直线与所成的角为60°；
（3）三棱锥体积的最大值是；
（4）当点自向处运动时，直线与平面所成的角逐渐增大.
三、解答题：本大题共6个小题，共85分.应写出文字说明，证明过程或演算步骤.
16.（本小题共15分）
已知函数，.
（Ⅰ）求；
（Ⅱ）函数的最小正周期；
（Ⅲ）求函数的最小值及相应的的值.
17.（本小题共15分）
在中，角，，所对的边分别为，，，已知，，.
（Ⅰ）求的值；
（Ⅱ）求的值；
（Ⅲ）求的面积.
18.（本小题共15分）
如图，在直三棱柱中，，，棱，为的中点.
（Ⅰ）求；
（Ⅱ）求直线与所成角的余弦值.
19.（本小题共15分）
如图，在长方体中，，，为的中点.
（Ⅰ）证明：；
（Ⅱ）求点到平面的距离；
（Ⅲ）求平面与平面夹角的余弦值
20.（本小题共13分）
如图，在四棱锥中，平面，，，，.为的中点，点在上，且.
（Ⅰ）求证：平面；
（Ⅱ）求直线与面所成角的正弦值；
（Ⅲ）在线段上是否存在点，使得、、、四点共面，如果存在求出的值；如果不存在说明理由.
21.（本小题共12分）
已知是棱长为的正四面体，设的四个顶点到平面的距离所构成的集合为，若中元素的个数为，则称为的阶等距平面，为的阶等距集.
（Ⅰ）若为的1阶等距平面且1阶等距集为，求的所有可能值以及相应的的个数；
（Ⅱ）已知为的4阶等距平面，且点与点，，分别位于的两侧.若的4阶等距集为，其中点到的距离为，求平面与夹角的余弦值.