

山西省大同市第一中学校2024-2025学年八年级上学期学业水平质量检测数学试题
展开
这是一份山西省大同市第一中学校2024-2025学年八年级上学期学业水平质量检测数学试题,共10页。试卷主要包含了试卷分第Ⅰ卷和第Ⅱ卷两部分,如图,人字梯的支架的长度都为,如图,已知,则判定的依据为等内容,欢迎下载使用。
数学
(监测内容:第十一至十二章)
注意事项:
1.试卷分第Ⅰ卷和第Ⅱ卷两部分.全卷共8页,满分120分,考试时间120分钟.
2.答案全部在答题卡上完成,答在本试卷上无效.
第Ⅰ卷选择题(共30分)
一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)
1.下列汽车标志中,不是由多个全等图形组成的是( )
A.B.C.D.
2.在直角三角形中,若其中一个锐角等于,则另一个锐角的度数为( )
A.B.C.D.
3.如图,人字梯的支架的长度都为(连接处的长度忽略不计),则两点之间的距离可能是( )
A.3mB.C.D.
4.如图,已知,则判定的依据为( )
A.SSSB.SASC.ASAD.AAS
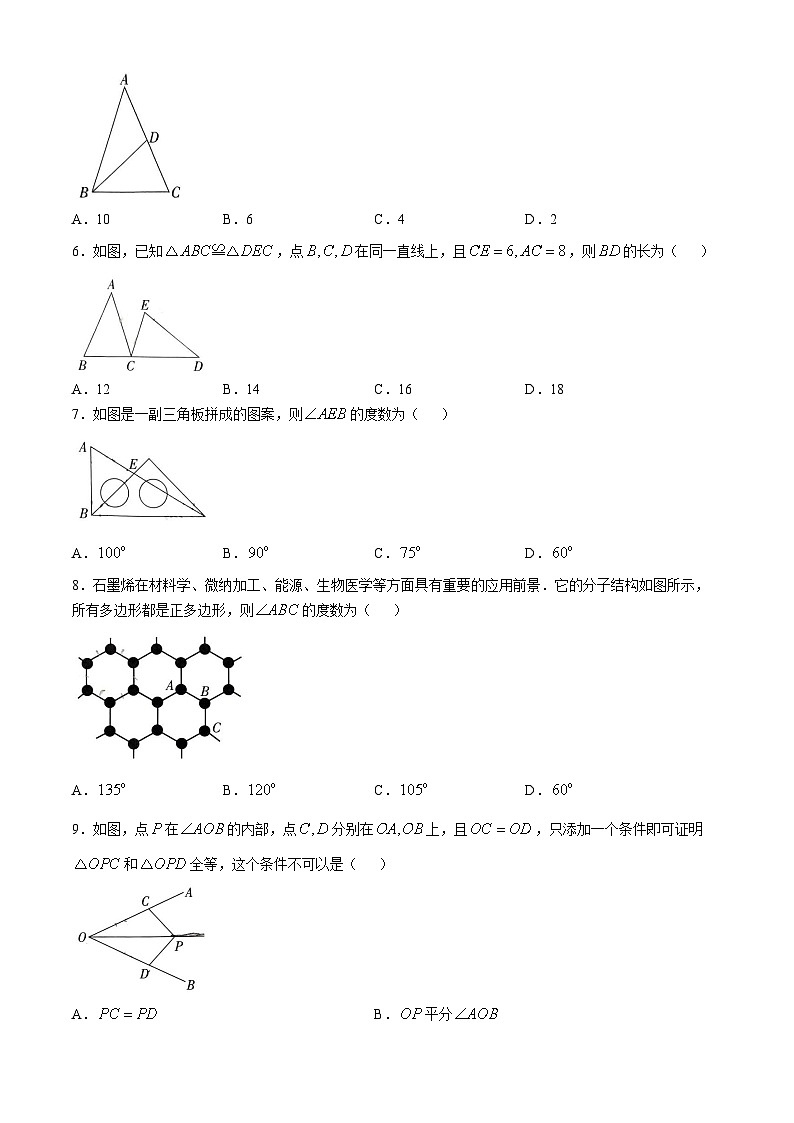
5.如图,是的中线,,则和的周长差为( )
A.10B.6C.4D.2
6.如图,已知,点在同一直线上,且,则的长为( )
A.12B.14C.16D.18
7.如图是一副三角板拼成的图案,则的度数为( )
A.B.C.D.
8.石墨烯在材料学、微纳加工、能源、生物医学等方面具有重要的应用前景.它的分子结构如图所示,所有多边形都是正多边形,则的度数为( )
A.B.C.D.
9.如图,点在的内部,点分别在上,且,只添加一个条件即可证明和全等,这个条件不可以是( )
A.B.平分
C.平分D.
10.“三角形的内角和为”是《几何原本》中的第五公设的推论,在探究证明这个定理时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是”的是( )
A.B.C.D.
第Ⅱ卷 非选择题(共90分)
二、填空题(本大题共5个小题,每小题3分,共15分)
11.数学来源于生活,又服务于生活.如图所示的椅子,将椅子脚设计成三角形,椅子非常稳固,其所利用的数学原理是_____
12.如图是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在三条_____的交点处.
13.方特海盗船是一种模拟海盗冒险场景的游乐项目.如图,当海盗船静止时,转轴到地面的距离.当海盗船的船头在处时,,此时测得点到地面的距离.当船头从处摆动到处时,,则点到的距离为_____m.
14.门窗是中国古代木构架建筑的重要组成部分.如图1所示是一款冰裂纹窗格,图2是窗格中的部分图案,其中是五边形的4个外角.若,则的度数是_____.
15.如图,在中,分别是上的点,且.若,则的度数为_____
三、解答题(本大题共8个小题,共75分,解答应写出文字说明、证明过程或演算步骤)
16.(本题6分)一个多边形的内角和比外角和的2倍多,求这个多边形的边数.
17.(本题8分)如图,已知为的中线.
(1)画出中边上的高;
(2)若,求的面积.
18.(本题8分)如图,于点于点交于点,连接.若,求证:平分.
19.(本题9分)如图,是边上的高,平分交于点,若,求和的度数.
20.(本题7分)怀仁塔(如图)北眺北魏古都大同,南望应县木塔,是二广高速路进入怀仁市的第一个标志性建筑,也是怀仁最美的一张名片.某校项目式学习小组开展项目活动测量怀仁塔底座(圆形平台)的直径,过程如下:
项目主题:测量怀仁塔底座的直径.
问题驱动:能利用哪些数学原理来测量底座的直径?
组内探究:由于底座中间不易到达,无法直接测量,需要借助一些工具来测量,比如自制的直角三角形硬纸板、米尺、测角仪、红外线水平仪等,甚至还可以利用无人机,确定方法后,先画出测量示意图,然后进行实地测量,记录数据,然后计算底座的直径.
成果展示:下面是同学们进行交流展示时的两种测量方案:
请你选择上述两种方案中的一种,计算怀仁塔底座的直径.
21.(本题10分)问题情境:
课外兴趣小组活动时,老师提出了如下问题:如图1,在中,若6,求边上的中线的取值范围.
操作探究:
(1)小明在组内经过合作交流,得到了如下的解决方法:延长到点,使,连接,请根据小明的思考方法补充完成下面的解题过程:
解:如图2,延长到点,使,连接.
因为是边上的中线,所以_____.
在和中,___________,,
所以.
所以_____,_____.
因为在中,,由三角形的三边关系,得,即.
所以__________.
方法总结:
(2)由(1)的解题过程,得到了一些启发,在解决类似问题时,条件中若出现“中点”“中线”字样,可以考虑倍长中线构造_____三角形,把分散的已知条件和所求的结论集中到同一个三角形中.
22.(本题13分)阅读与思考
阅读下列材料,并完成相应的任务.
多边形分为凸多边形和凹多边形.
如果将一个多边形的任意一条边向两方无限延长成为一条直线时,其他各边都在此直线的同旁,那么这个多边形就叫做凸多边形.
如果一个多边形的所有边中有一条边向两方无限延长成为一条直线时,其他各边不都在此直线的同旁,那么这个多边形就叫做凹多边形.
我们知道,探索多边形内角和的方法是将其转化为三角形,利用三角形内角和获得结论,这一方法也可以用来解决其他求角度的问题.
如图,四边形是凸四边形,探究其内角和的方法是:连接对角线,则四边形内角和就转化为与内角和相加,为.
任务一:在上述阅读材料的探究过程中,体现了数学中的_____.
A.整体思想B.方程思想
C.转化思想D.分类讨论思想
任务二:如图1,四边形是凹四边形,请探究与,三个角之间的等量关系.
小明得出的结论是:.请你将下面小明的证明过程补充完整.
证明:如图1,连接并延长到点.
……
任务三:图2中的度数为_____.
23.(本题14分)综合与探究
如图1,在四边形中,是上一点,是的延长线上一点,且.
(1)求证:;
(2)如图2,若点在上,且,试猜想之间的数量关系,并说明理由;
(3)如图3,若题目中的“”改成“”,点在上,则满足什么条件时,(2)中的结论仍然成立?请说明理由.
山西省2024—2025学年第一学期八年级学业水平质量监测
数学试题参考答案及评分建议
说明:本评分标准每题给出了一种解法供参考,如果考生的解法与本解答不同,参照本评分标准的精神给分.
一、选择题(本大题共10个小题,每小题3分,共30分)
二、填空题(本大题共5个小题,每小题3分,共15分)
11.三角形具有稳定性12.角平分线13.614.15.
三、解答题(本大题共8个小题,共75分)
16.(本题6分)
解:设这个多边形的边数为.
根据题意,得.
解得.
答:该多边形的边数为7.
17.(本题8分)
解:(1)如图所示:
(2)因为为的高,所以.
因为为的中线,所以.
18.(本题8分)
证明:因为,所以.
在和中,,所以(AAS).
所以.
又因为,所以平分.
19.(本题9分)
解:因为是边上的高,所以.
所以.
因为平分,所以.
所以.
20.(本题7分)
解:选择方案①.
因为,所以.
在和中,,
所以(ASA).
因为,所以.
所以怀仁塔底座的直径为.
选择方案②.
在和中,,
所以(SAS).
因为,所以.
所以怀仁塔底座的直径为.
21.(本题10分)
解:(1)依次填:.
(2)全等
22.(本题13分)
解:任务一
任务二 证明:连接AD并延长到点E.
所以为的外角,为的外角.
所以.
所以.
任务三 .
23.(本题14分)
解:(1)证明:因为,所以.
因为,所以.
在和中,,所以(SAS).
所以.
(2).
理由如下:
由(1)得,所以.
因为,所以.
所以,即.
在和中,,,,所以(SAS).
所以.
因为,所以.
(3)当时,(2)中结论仍然成立.
理由如下:
因为,所以.
同(1)可证.所以.
因为,所以.
所以,即.
同(2)可证.所以.
因为,所以.
测量示意图
测量说明
测量结果
方案①
图1
如图1,测量员在地面上找一点,在连线的中点处做好标记,从点出发,沿着与平行的直线向前走到点处,使得点,在一条直线上,测出的长
,,
方案②
图2
如图2,测量员在地面上找一点,沿着向前走到点处,使得,沿着向前走到点处,使得,测出两点之间的距离
,,
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
A
C
D
B
C
B
C
B
相关试卷
这是一份山西省大同市第一中学校2024-2025学年八年级上学期学业水平质量检测数学试题,文件包含山西省大同市第一中学校2024-2025学年八年级上学期学业水平质量检测数学试题pdf、2024秋山西八年级数学月考一评分标准pdf等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。
这是一份山西省大同市第一中学校2024-2025学年八年级上学期10月月考数学试题,文件包含山西省大同市第一中学校2024-2025学年八年级上学期10月月考数学试题pdf、山西省大同市第一中学校2024-2025学年八年级上学期10月月考数学试题答案pdf等2份试卷配套教学资源,其中试卷共9页, 欢迎下载使用。
这是一份2024-2025学年山西省大同市第一中学九上数学开学教学质量检测试题【含答案】,共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








