
河南省周口市部分学校2024-2025学年高二上学期阶段性测试(一)(10月)数学试题(无答案)
展开
这是一份河南省周口市部分学校2024-2025学年高二上学期阶段性测试(一)(10月)数学试题(无答案),共4页。试卷主要包含了将直线绕点等内容,欢迎下载使用。
考生注意:
1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上,并将考生号条形码粘贴在答题卡上的指定位置.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.图中4条直线中斜率最小的是( )
A. B.C.D.
2.已知向量与平行,则( )
A.B.C.3D.15
3.已知直线的一个方向向量为,平面的一个法向量为,若∥,则( )
A.1B.2C.3D.4
4.将直线绕点(1,3)逆时针旋转rad后所得直线的方程为( )
A.B.C.D.
5.已知平面均以为法向量,平面经过坐标原点,平面经过点,则平面与的距离为( )
A.2B.C.3D.
6.已知直线与平行,且之间的距离与点到的距离均为1,则在轴上的截距为( )
A.B.0C.1D.4
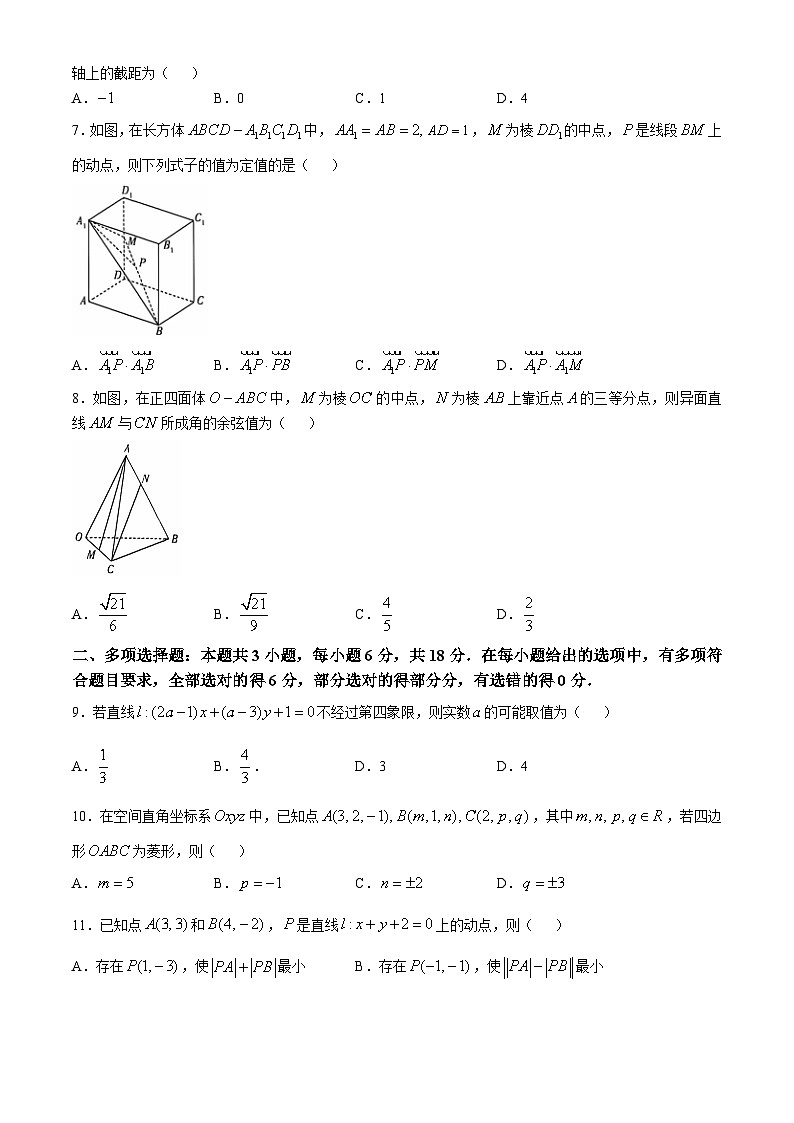
7.如图,在长方体中,,为棱的中点,是线段上的动点,则下列式子的值为定值的是( )
A.B. C. D.
8.如图,在正四面体中,为棱的中点,为棱上靠近点的三等分点,则异面直线与所成角的余弦值为( )
A.B. C.D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.若直线不经过第四象限,则实数的可能取值为( )
A. B..D.3D.4
10.在空间直角坐标系中,已知点,其中,若四边形为菱形,则( )
A.B.C.D.
11.已知点和,是直线上的动点,则( )
A.存在,使最小B.存在,使最小
C.存在,使最大D.存在,使最小
三、填空题:本题共3小题,每小题5分,共15分.
12.已知向量,若,则________.
13.已知,平面内三点共线,则________.
14.已知正四棱柱的体积为4,侧面积为8,动点分别在线段上,则线段长度的最小值是________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
已知空间中三点,设向量.
(I)若,求实数的值;
(Ⅱ)若向量与共线,且,求的坐标.
16.(15分)
已知直线的方程为,直线经过点和.
(I)若,求的值;
(Ⅱ)若当变化时,总过定点,求.
17.(15分)
如图,在四棱锥中,底面为正方形,为等边三角形,且为棱的中点.
(1)证明:平面平面;
(Ⅱ)求直线与平面所成角的正弦值.
18.(17分)
如图,将一块三角形的玉石置于平面直角坐标系中,已知,点,图中阴影三角形部分为玉石上的瑕疵,为了将这块玉石雕刻成工艺品,要先将瑕疵部分切割掉,可沿经过点的直线进行切割.
(I)求直线的倾斜角的取值范围.
(Ⅱ)是否存在直线,使得点关于直线的对称点在线段上?
(Ⅲ)设玉石经切割后剩余部分的面积为,求的取值范围.
19.(17分)
在空间直角坐标系中,过点且以为方向向量的直线方程可表示为,过点且以为法向量的平面方程可表示为.
(1)若直线:与都在平面内,求平面的方程;
(Ⅱ)在三棱柱中,点与坐标原点重合,点在平面内,平面以为法向量,平面的方程为,求点的坐标;
(Ⅲ)若集合中所有的点构成了多面体的各个面,求的体积和相邻两个面所在平面的夹角的余弦值.
相关试卷
这是一份湖南省郴州市部分学校2024-2025学年高二上学期第一次月考数学试题(无答案),共4页。试卷主要包含了本试卷主要考试内容,在正方体中,二面角的正切值为,已知函数,则等内容,欢迎下载使用。
这是一份河南省周口市周口学校2024-2025学年高二上学期9月月考数学试题,共15页。试卷主要包含了设,向量,,且,,则等内容,欢迎下载使用。
这是一份河南省周口市周口学校2024-2025学年高二上学期9月月考数学试题,文件包含2024-2025学年河南省部分学校考试高二上学期9月数学试题pdf、数学人教版高二9月联考答案pdf等2份试卷配套教学资源,其中试卷共11页, 欢迎下载使用。








