辽宁省锦州市实验学校2024-2025学年九年级上学期10月考数学试题

这是一份辽宁省锦州市实验学校2024-2025学年九年级上学期10月考数学试题，共14页。试卷主要包含了若，则的值为，下列判断中不正确的是，一元二次方程的根的情况是等内容，欢迎下载使用。
请在答题卡内作答
一．选择题（共10小题，每小题3分，共30分）
1．若，则的值为（ ）
A．B．C．D．
2．如图，小东展示了“过直线外一点作已知直线的平行线”的尺规作图过程，点为直线上一点，过点的一条直线分别交两条平行线于点，，则有，这一步的依据是（ ）
第2题图
A．同位角相等，两直线平行B．三角形中位线定理
C．平行线分线段成比例D．相似三角形的对应边成比例
3．下列判断中不正确的是（ ）
A．对角线互相垂直平分的四边形是正方形
B．四个角相等的四边形是矩形
C．对角线互相平分的四边形是平行四边形
D．对角线互相垂直的平行四边形是芠形
4．一元二次方程的根的情况是（ ）
A．有两个相等的实数根
B．有两个不相等的实数根
C．没有实数根
D．只有一个实数根
5．某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送1035张照片，如果全班有名同学，根据题意，列出方程为（ ）
A．B．
C．D．
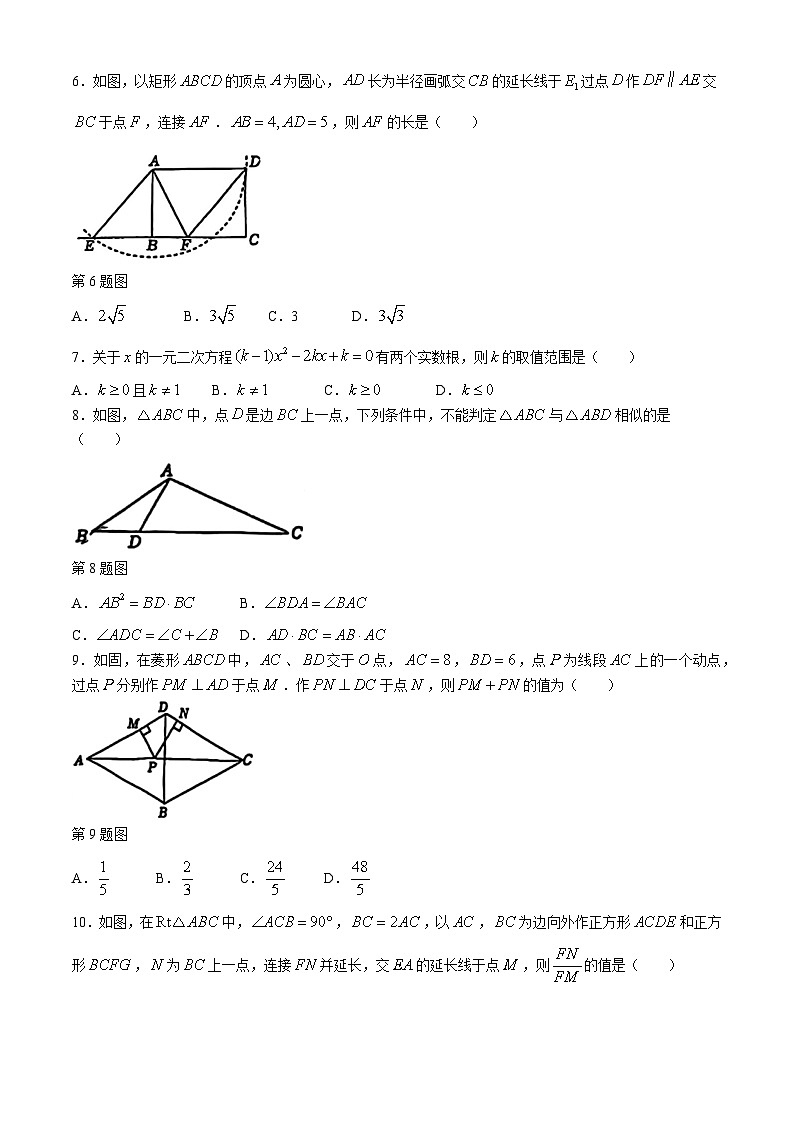
6．如图，以矩形的顶点为圆心，长为半径画弧交的延长线于过点作交于点，连接．，则的长是（ ）
第6题图
A．B．C．3D．
7．关于的一元二次方程有两个实数根，则的取值范围是（ ）
A．且B．C．D．
8．如图，中，点是边上一点，下列条件中，不能判定与相似的是（ ）
第8题图
A．B．
C．D．
9．如固，在菱形中，、交于点，，，点为线段上的一个动点，过点分别作于点．作于点，则的值为（ ）
第9题图
A．B．C．D．
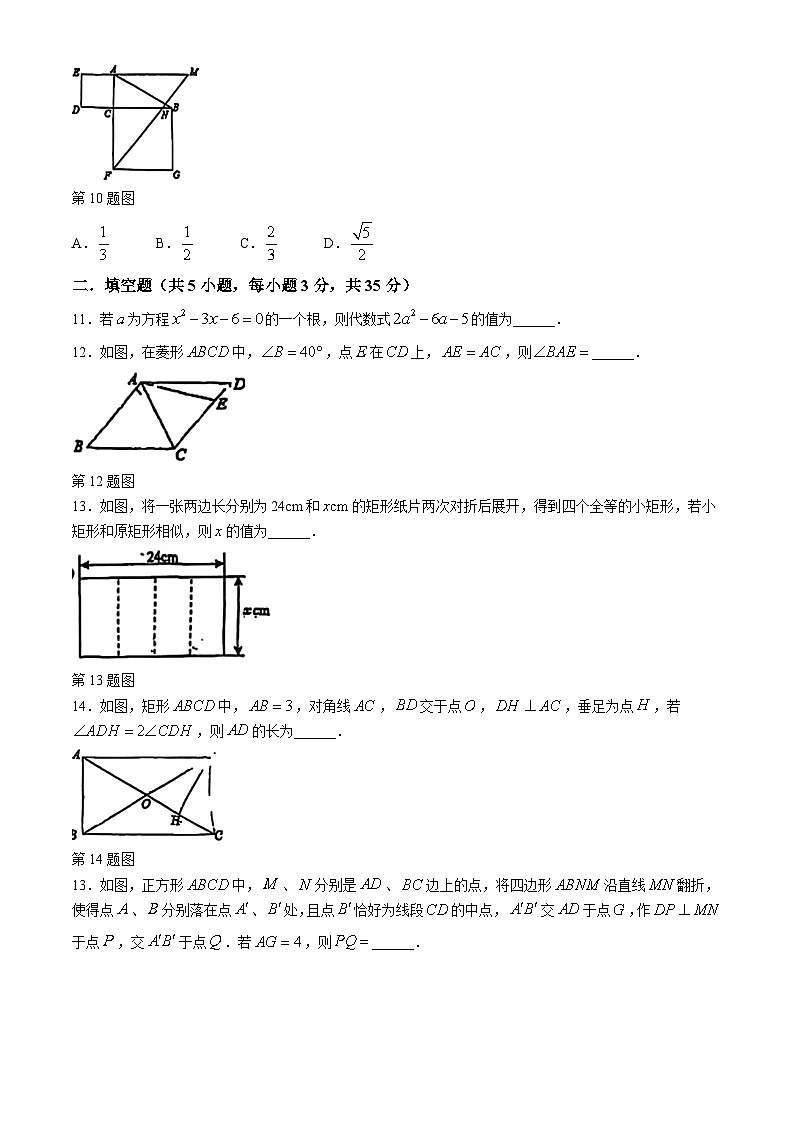
10．如图，在中，，，以，为边向外作正方形和正方形，为上一点，连接并延长，交的延长线于点，则的值是（ ）
第10题图
A．B．C．D．
二．填空题（共5小题，每小题3分，共35分）
11．若为方程的一个根，则代数式的值为______．
12．如图，在菱形中，，点在上，，则______．
第12题图
13．如图，将一张两边长分别为24cm和的矩形纸片两次对折后展开，得到四个全等的小矩形，若小矩形和原矩形相似，则的值为______．
第13题图
14．如图，矩形中，，对角线，交于点，，垂足为点，若，则的长为______．
第14题图
13．如图，正方形中，、分别是、边上的点，将四边形沿直线翻折，使得点、分别落在点、处，且点恰好为线段的中点，交于点，作于点，交于点．若，则______．
第15题
三．解答题（共8小题，共75分）
16．（8分）用适当的方法解下列方程：
（1）；（2）．
17．（7分）现要在一个长为38m，宽为24m的矩形花园中修建等宽的小道，剩余的地方种植花草．如图所示，要使种植花草的面积为828m2，求小道的宽度．
18．为解决问题：邓州公安交通部门提醒市民，骑车出行必须严格遵守“一盔一带”的规定．某头盔经销商统计了某品牌头盔7月份到9月份的销量，该品牌头盔7月份销售500个，9月份销售720个，且从7月份到9月份销售量的月增长率相同．
（1）求该品牌头盔销售量的月增长率．
（2）若此种头盔的进价为30元/个，经市场预测，当售价为40元/个时，月销售量为600个，若在此基础上售价每上涨1元/个，则月销售量将减少10个，为使月销售利润达到10000元，而且尽可他让顾客得到实惠，该品牌头盔的实际售价应定为多少元？
19．（9分）如图，在中，为线段的中点，延长交的延长线于点，连接；
（1）求证：四边形是矩形；
（2）连接，若，，求的长．
20．（9分）如图，在中，于，为上一点，且．
（1）求证：；
（2）．若，，，求的长．
21．（9分）若某个一元二次方程的两根都是整数，且其中一根是另一根的整数倍，则称该方程是“倍根方程”．例如的两根为，因为是的－3倍，所以是“倍根方程”．
（1）说明是“倍根方程”；
（2）已知是正整数，若关于的一元二次方程是“倍根方程”，且关于的一元二次方程总有两个不相等的实数根，求的值．
22．（12分）如图①，在正方形ABCD中，点N、M分别在边BC、CD上，连结AM、MN，
∠MAN＝45°，将△AMD绕点A顺时针旋转90°，点D与点B重合，得到△ABE．易证：△ANM≌△ANE，从而得DM+BN＝MN．
【实践探究】
（1）在图①条件下，若CN＝6，CM＝8，则正方形ABCD的边长是_______．
（2）如图②，点M、N分别在边CD、AB上，且BN＝DM．点E、F分别在BM、DN上，∠EAF＝45°，连接EF，猜想三条线段EF、BE、DF之间满足的数量关系，并说明理由．
【拓展应用】
（3）如图③，在矩形ABCD中，AB＝6，AD＝8，点M、N分别在边DC、BC上．连结AM，AN，已知∠MAN＝45°，BN＝2，求DM的长．
23．（12分）【阅读理解】
定义：在同一平面内，有不在同一条直线上的三点，，，连接，，设，，则我们把称为点到关于点的“度比坐标”，把称为点到关于点的“度比坐标”．
【迁移运用】
如图，直线分别与轴，轴相交于，两点，过点的直线与在第一象限内相交于点．根据定义，我们知道点到关于点的“度比坐标”为．
（1）请分别管接写出，两点的坐标及点到关于点的“度比坐标”；
（2）若点到关于点的“度比坐标”与点到关于点的“度比坐标”相同．
①求直线的函数表达式；
②点，分别是直线，上的动点，连接，，若点到关于点的“度比坐标”为，求此时点的坐标．
2024－2025学年度九上核心素养测评数学试卷参考答案
一．选择题（共10小题，每小题3分，共30分）
二．填空题（共5小题，每小题3分，共15分）
11．712．11012．1214．15．
三．解答题（共8小题，共75分）
16．（8分）用适当的方法解下列方程：
解：（1）．．
或，．；
（2）．
整理得：．
，，．
．
．
．
（注：按步骤给分）
17．（7分）解：设小道的宽度为m，则．
整理得．解得，（不符合实际，舍去）．
答：小道的宽度为1m．
18．（9分）解：（1）设该品牌头盔销售量的月增长为x．依题意，得：
．
解得：．（不符合题意，舍去）．
答：该品牌头盔销售量的月增长率为20%．
（2）设该品解头盔的实际售价为y元，依题意，得：
．
整理，得：．
解得：（不合题意，舍去）．．
答：该品牌头盔的实际售价应定为50元．
19．（9分）（1）评明：为的中点．
．
四边形是平行四边形．
．
．
又．
．
．
四边形是平行四边形．
．
．
平行四边形ABDE是矩形．
（2）解：加图．过点作点．
四边形是矩形．
．．，．
．
．
．
为的中位线．
．
四边形是平行四边形．
．
．
在中．．
．
20．（9分）（1）证明：四边形是平行四边形．
．
，．
，．
．
．
（2）解：．．
．
．
．
在中，
．
．
（负值舍去）．
．
．
．．
21．（9分）解：
（1）．
．
或．解得：．
，
是“倍根方程”．
（2）
或
解得：，
总有两个不相等的实数根，
解得：，
是正整数，
方程是“倍根方程”．
能被整除或能被2整除．
或3．
22．（12分）解：（1）12；
（2）．
理由如下：
如图②，将绕点顺时针旋转，点与点重合，得到，连接，
．
．
．
又
，
四边形是平行四边形．
．
．
．
．
．
．
（3）如图③，延长至，使，过作的平行线交的延长线于．延长交于．连接．
则四边形正方形，
．
设，则．
．
．
．
．
．
由（1）得：．
在中，．
解得：，
即的长是4．
23．（12分）解：（1）在中，令时，，令时，，
点到关于点的“度比坐标”为．
（2）（i）过作轴于，连接，如图：
．
点到关于点的“度比坐标”与点到关于点的“度比坐标”相同，
，
．
．
，即．
轴于，
．
．
．
．
在中，令得，．
设直线的函数表达式为，将，，代入得：
．解得．
直线的函数表达式为．
（ⅱ）当在轴上方时．过作轴于，过作轴于，如图：
点到关于点的“度比坐标”为．
．
．又．
．．
设．则．
．．．
把代入得：
．解得．．
当，在轴下方时，过作轴于，过作轴于，如图：
设，则，
同理可得．．
解得．．综上所述，的坐标为或．
题号
1
2
3
4
5
6
7
8
9
10
答案
C
C
A
A
C
A
A
D
C
C