北京市第一七一中学2024~2025学年上学期九年级月考数学试卷（10月份）(无答案)

这是一份北京市第一七一中学2024~2025学年上学期九年级月考数学试卷（10月份）(无答案)，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本题共16分，每小题2分）
1.风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心O旋转n°后能与原来的图案重合，那么n的值可能是（ ）
A.120B.90C.60D.45
2.用配方法解方程，变形后结果正确的是（ ）
A.B.C.D.
3.将抛物线向右平移3个单位，再向上平移1个单位得到的解析式是（ ）
A.B.C.D.
4.根据圆规作图的痕迹，可用直尺成功找到三角形内心的是（ ）
A.B.C.D.
5.同时抛掷两枚质地均匀的硬币，则一枚硬币正面向上、一枚硬币反面向上的概率是（ ）
A.B.C.D.
6.如图，点A、B、C都在上，若，则的度数（ ）
A.30°B.150°C.105°D.110°
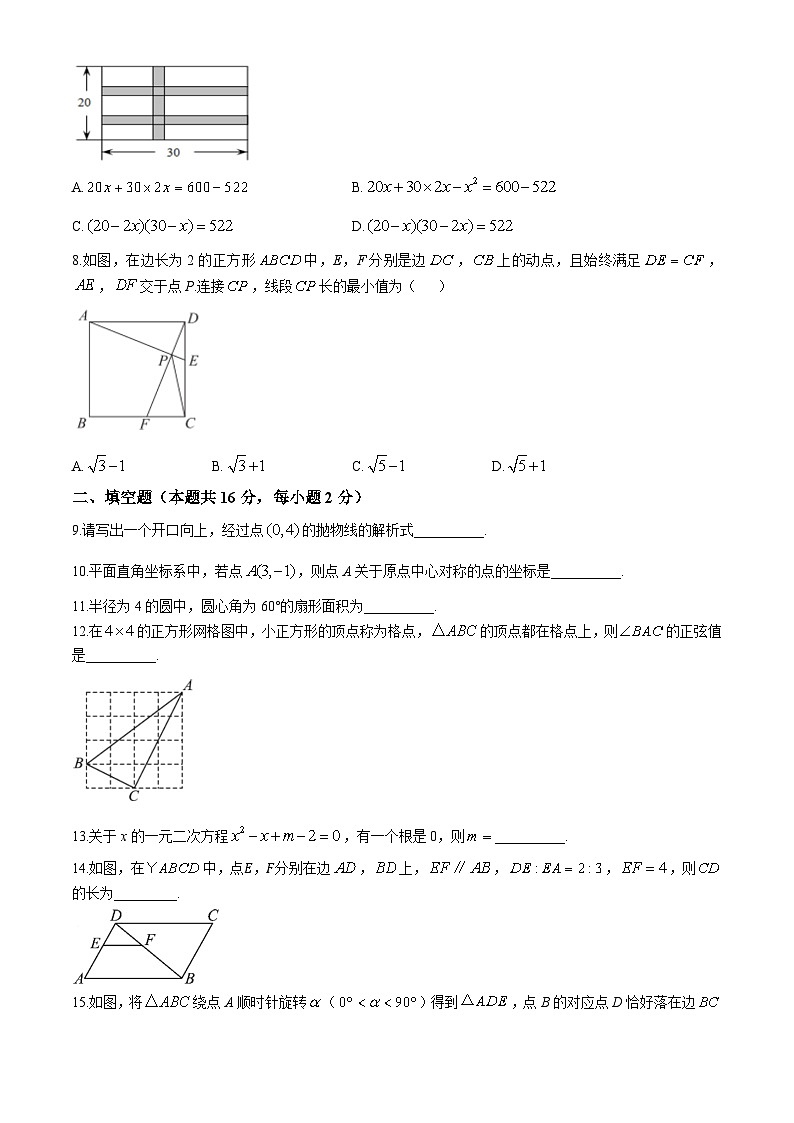
7.如图，在一块长30m，宽20m的矩形苗圃基地上修建两横一纵三条等宽的道路，剩余空地种植花苗，设道路的宽为m，若种植花苗的面积为522，依题意列方程（ ）
A.B.
C.D.
8.如图，在边长为2的正方形中，E，F分别是边，上的动点，且始终满足，，交于点P.连接，线段长的最小值为（ ）
A.B.C.D.
二、填空题（本题共16分，每小题2分）
9.请写出一个开口向上，经过点的抛物线的解析式__________.
10.平面直角坐标系中，若点，则点A关于原点中心对称的点的坐标是__________.
11.半径为4的圆中，圆心角为60°的扇形面积为__________.
12.在的正方形网格图中，小正方形的顶点称为格点，的顶点都在格点上，则的正弦值是__________.
13.关于x的一元二次方程，有一个根是0，则__________.
14.如图，在中，点?，?分别在边，上，，，，则的长为_________.
15.如图，将绕点A顺时针旋转（）得到，点B的对应点D恰好落在边上，则________.（用含的式子表示）
16.某校今年“节”策划了五个活动，规则见下图：
小云参与了所有活动.
（1）若小云只挑战成功一个，则挑战成功的活动名称为__________；
（2）若小云共挑战成功两个，且她参与的第四个活动成功，则小云最终剩下的“币”数量的所有可能取值为_________.
三、解答题（本题共68分，17-22题每小题5分，23-26题每题6分，27、28题每题7分）
17.解一元二次方程：
18.下面是“过圆外一点作圆的切线”的尺规作图过程.

图1 图2
已知：如图1，和外一点P.
求作：过点P的的切线.
作法：如图2，
（1）连结，作线段的中点M；
（2）以M为圆心，的长为半径作圆，交于点A，B；
（3）作直线和.
直线，即为所求作的切线.
请在图2中补全图形，并完成下面的证明.
证明：连接
由作法可知，为的直径，
∴（_________________________）（填推理的依据）
∴
∵点A在上
∴直线是圆的切线（_________________________）（填推理的依据）
同理，直线也是圆的切线.
19.如图，为的直径，弦于点E，若，，求半径的长.
20.已知二次函数.
（1）补全表格，并在平面直角坐标系中用描点法画出该函数图象；
（2）根据图象回答：时，x的取值范围是_____________；
（3）根据图象回答：当时，y的取值范围是_____________.
21.如图，三个顶点的坐标分别为，，.
（1）请在图中作出绕点A逆时针方向旋转90°后得到的图形；
（2）求点C运动到点所经过的路径的长（结果保留）.
22.已知关于x的一元二次方程.
（1）求证：方程总有两个实数根；
（2）若方程有一个根小于1，求m的取值范围.
23.某学校举办航天知识讲座，需要两名引导员，决定从A，B，C，D四名志愿者中，通过抽签的方式确定两人.抽签规则：将四名志愿者的名字分别写在四张完全相同且不透明卡片的正面，把四张卡片背面朝上，洗匀后放在桌面上，先从中随机抽取一张卡片，记下名字，再从剩余的三张卡片中随机抽取第二张，记下名字.
（1）“A志愿者被选中”是________事件（填“随机”或“不可能”或“必然”）；
（2）用画树状图或列表的方法求出A，B两名志愿者同时被选中的概率.
24.某公园在在垂直于湖面的立柱上安装了一个多孔喷头，从喷头每个孔喷出的水柱形状相同，可以看作是抛物线的一部分，当喷头向四周同时喷水时，形成一个环状喷泉.安装通过测量其中一条水柱，获得如下数据，在距立柱水平距离为d米的地点，水柱距离湖面高度为h米.请解决以下问题：
（1）在网格中建立适当的平面直角坐标系，根据已知数据描点，并用平滑的曲线连接；

（2）结合表中所给数据或所画图象，直接写出这条水柱最高点距离湖面的高度________；
（3）求所画图象对应的函数表达式；
（4）从安全的角度考虑，需要在这组喷泉外围设立一圈正方形护栏，这个喷泉的任何一条水柱在湖面上的落点到护栏的距离不能小于1米，请通过计算说明公园至少需要准备多少米的护栏（不考虑接头等其他因素）.
25.如图，已知为的直径，D是上的一点，且点C是弧的中点，过点C作直线于点E.
（1）求证：直线是的切线；
（2）连接，过点O作于F，延长交于M，若B为弧的中点，半径为4，求的长.
26.在平面直角坐标系中，已知抛物线（）.
（1）若抛物线过点，求该抛物线的对称轴；
（2）若，，在抛物线上，且满足，当抛物线对称轴为直线时，求t的取值范围.
27.如图，在中，，，过点A作的垂线，垂足为D，E为线段上一动点（不与点C重合），连接，以点A为中心，将线段逆时针旋转90°得到线段，连接，与直线交于点G.
（1）依题意补全图形；并直接写出与的位置关系;
（2）求证：点G为的中点.
（3）写出，，之间的数量关系，并证明.
28.在平面直角坐标系中，已知点A和B，对于点P定义如下：以点A为对称中心作点P的对称点，再将对称点绕点B逆时针旋转90°，得到点Q，称点Q为点P的反转点.
（1）如图，点，，点，点Q为点P的反转点.
①当时，在图中画出点Q，并写出点Q的坐标为________；
②当时，求线段长的取值范围；
（2）已知的半径为，点A是上一点，点B和P是外两个点，点Q为点P的反转点.若点P在第一象限内，点B在第四象限内，当点A在上运动时，直接写出线段长的最大值和最小值的差.
x
…
-1
0
1
2
3
…
y
…
0
3
…
d（米）
0
1.0
3.0
5.0
7.0
h（米）
3.2
4.2
5.0
4.2
1.8