2025届云南省腾冲市第八中学九上数学开学达标检测模拟试题【含答案】

这是一份2025届云南省腾冲市第八中学九上数学开学达标检测模拟试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）下列式子中，属于最简二次根式的是( )
A．B．C．D．
2、（4分）.一支蜡烛长20m,点燃后每小时燃烧5厘米,燃烧时剩下的高度(厘米)与燃烧时间(时)的函数关系的图像是
A．B．C．D．
3、（4分）如图，小明在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于的长为半径画弧，两弧相交于C、D两点，直线CD即为所求．根据他的作图方法可知四边形一定是（ ）
A．矩形B．菱形C．正方形D．无法确定
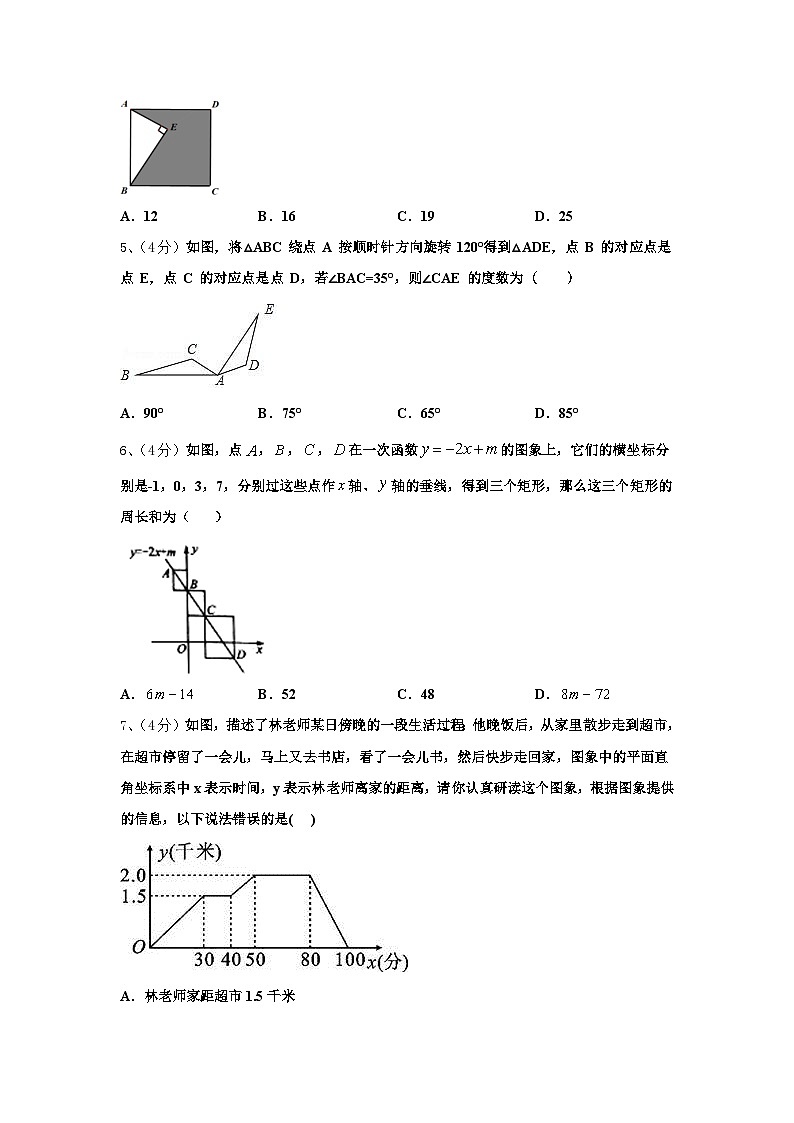
4、（4分）如图，点E在正方形ABCD内，满足∠AEB=90°，AE=3，BE=4，则阴影部分的面积是（ ）
A．12B．16C．19D．25
5、（4分）如图，将△ABC 绕点 A 按顺时针方向旋转 120°得到△ADE，点 B 的对应点是点 E，点 C 的对应点是点 D，若∠BAC=35°，则∠CAE 的度数为（ ）
A．90°B．75°C．65°D．85°
6、（4分）如图，点，，，在一次函数的图象上，它们的横坐标分别是-1，0，3，7，分别过这些点作轴、轴的垂线，得到三个矩形，那么这三个矩形的周长和为（ ）
A．B．52C．48D．
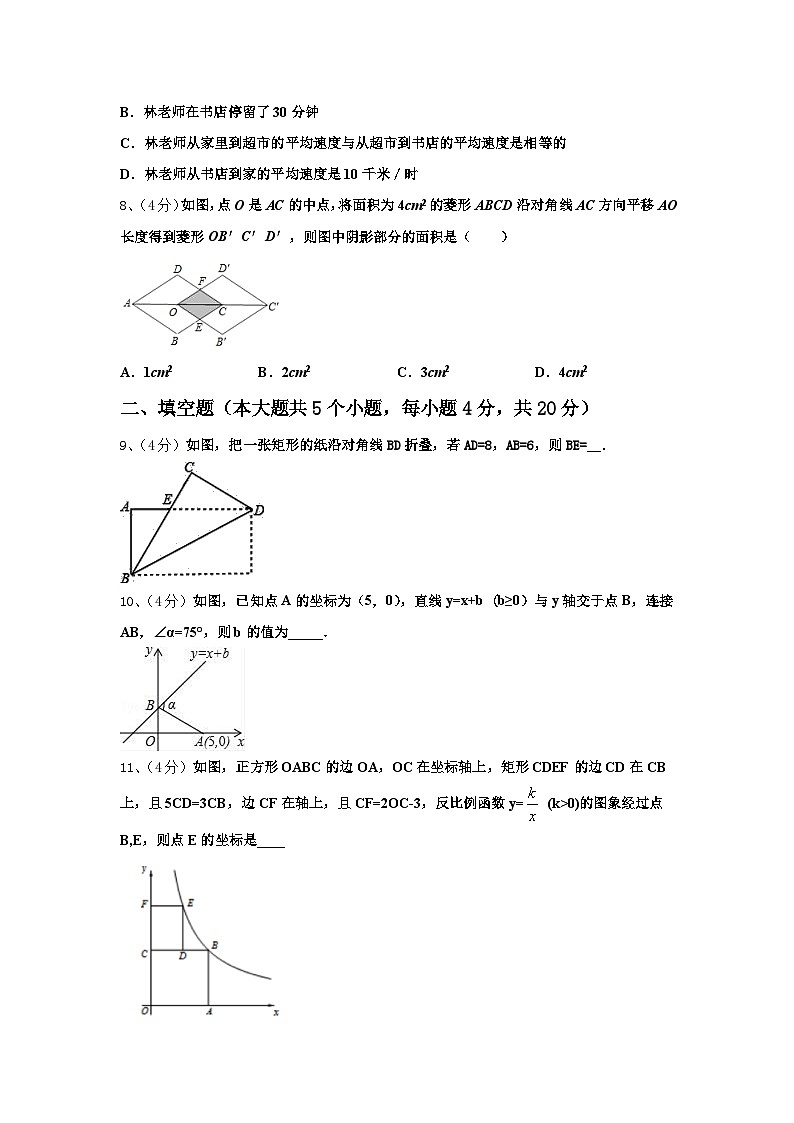
7、（4分）如图，描述了林老师某日傍晚的一段生活过程：他晚饭后，从家里散步走到超市，在超市停留了一会儿，马上又去书店，看了一会儿书，然后快步走回家，图象中的平面直角坐标系中x表示时间，y表示林老师离家的距离，请你认真研读这个图象，根据图象提供的信息，以下说法错误的是( )
A．林老师家距超市1.5千米
B．林老师在书店停留了30分钟
C．林老师从家里到超市的平均速度与从超市到书店的平均速度是相等的
D．林老师从书店到家的平均速度是10千米／时
8、（4分）如图，点O是AC的中点，将面积为4cm2的菱形ABCD沿对角线AC方向平移AO长度得到菱形OB′C′D′，则图中阴影部分的面积是（ ）
A．1cm2B．2cm2C．3cm2D．4cm2
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，把一张矩形的纸沿对角线BD折叠，若AD=8，AB=6，则BE=__．
10、（4分）如图，已知点A的坐标为（5，0），直线y=x+b（b≥0）与y轴交于点B，连接AB，∠α=75°，则b的值为_____．
11、（4分）如图，正方形OABC的边OA，OC在坐标轴上，矩形CDEF的边CD在CB上，且5CD=3CB，边CF在轴上，且CF=2OC-3，反比例函数y= (k>0)的图象经过点B,E，则点E的坐标是____
12、（4分）已知实数、满足，则_____．
13、（4分）已知的面积为27，如果，，那么的周长为__________．
三、解答题（本大题共5个小题，共48分）
14、（12分）某学校需要置换一批推拉式黑板，经了解，现有甲、乙两厂家报价均为100元/米1，且提供的售后服务完全相同，为了促销，甲厂家表示，每平方米都按七折计费；乙厂家表示，如果黑板总面积不超过10米1，每平方米都按九折计费，超过10米1，那么超出部分每平方米按六折计费．假设学校需要置换的黑板总面积为x米1．
（1）请分别写出甲、乙两厂家收取的总费用y（元）与x（米1）之间的函数关系式；
（1）请你结合函数图象的知识帮助学校在甲、乙两厂家中，选择一家收取总费用较少的．
15、（8分）已知ABC为等边三角形，点D、E分别在直线AB、BC上，且AD=BE.
（1）如图1，若点D、E分别是AB、CB边上的点，连接AE、CD交于点F，过点E作∠AEG=60°，使EG=AE，连接GD，则∠AFD= （填度数）；
（2）在（1）的条件下，猜想DG与CE存在什么关系，并证明；
（3）如图2，若点D、E分别是BA、CB延长线上的点，（2）中结论是否仍然成立？请给出判断并证明.
16、（8分）如图，在平行四边形ABCD中，点E，F分别是AB，CD的中点．
（1）求证：四边形AEFD是平行四边形；
（2）若∠DAB＝120°，AB＝12，AD＝6，求△ABC的面积．
17、（10分）如图，直线与轴交于点，与轴交于点；直线与轴交于点，与直线交于点，且点的纵坐标为4.
（1）不等式的解集是 ；
（2）求直线的解析式及的面积；
（3）点在坐标平面内，若以、、、为顶点的四边形是平行四边形，求符合条件的所有点的坐标.
18、（10分）如图，根据要求画图．
（1）把向右平移5个方格，画出平移的图形．
（2）以点B为旋转中心，把顺时针方向旋转，画出旋转后的图形．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）某同学在体育训练中统计了自己五次“1分钟跳绳”成绩，并绘制了如图所示的折线统计图，这五次“1分钟跳绳”成绩的中位数是__________个．
20、（4分）如图，每一幅图中均含有若干个正方形，第1幅图中有1个正方形；第2幅图中有1+4＝5个正方形；第三幅图中有1+4+9＝14个正方形；…按这样的规律下去，第4幅图中有_____个正方形．
21、（4分）如图，平行四边形ABCD中，，，AE平分交BC于点E，则CE的长为______.
22、（4分）某商场品牌手机经过5、6月份连续两次降价，每部售价由5000元降到4050元，设平均每次降价的百分率为x，根据题意可列方程：_____．
23、（4分）在平面直角坐标系中，P（2，﹣3）关于x轴的对称点是_____
二、解答题（本大题共3个小题，共30分）
24、（8分）先化简，再求值，其中．
25、（10分）在△ABC中，∠C＝90°，AC＝6，BC＝8，D、E分别是斜边AB和直角边CB上的点，把△ABC沿着直线DE折叠，顶点B的对应点是B′．
（1）如图（1），如果点B′和顶点A重合，求CE的长；
（2）如图（2），如果点B′和落在AC的中点上，求CE的长．
26、（12分）如图，点E，F在矩形的边AD，BC上，点B与点D关于直线EF对称．设点A关于直线EF的对称点为G．
（1）画出四边形ABFE关于直线EF对称的图形；
（2）若∠FDC＝16°，直接写出∠GEF的度数为 ；
（3）若BC＝4，CD＝3，写出求线段EF长的思路．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
分析：检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．
详解：A.被开方数含能开得尽方的因数或因式，故不符合题意；
B. 被开方数含分母，故不符合题意；
C.被开方数含分母，故不符合题意；
D. 被开方数不含分母；被开方数不含能开得尽方的因数或因式，故符合题意；
故选D.
点睛：此题考查了最简二次根式：被开方数不含分母；被开方数不含能开得尽方的因数或因式，满足这两个条件的二次根式才是最简二次根式.
2、D
【解析】
燃烧时剩下高度h（cm）与燃烧时间t（小时）的关系是：h=20-5t （0≤t≤4），图象是以（0，20），（4，0）为端点的线段．
【详解】
解：燃烧时剩下高度h（cm）与燃烧时间t（小时）的关系是：h=20-5t （0≤t≤4），
图象是以（0，20），（4，0）为端点的线段．
故选：D．
此题首先根据问题从图中找出所需要的信息，然后根据燃烧时剩下高度h（cm）与燃烧时间t（小时）的关系h=20-5t （0≤t≤4），做出解答．
3、B
【解析】
根据菱形的判定方法：四边都相等的四边形是菱形判定即可.
【详解】
根据作图方法可得：,
因此四边形ABCD一定是菱形.
故选：B
本题考查了菱形的判定，解题的关键在于根据四边相等的四边形是菱形判断.
4、C
【解析】
根据勾股定理求出AB，分别求出△AEB和正方形ABCD的面积，即可求出答案．
【详解】
解：∵在Rt△AEB中，∠AEB=90°，AE=3，BE=4，
由勾股定理得：AB==5，
∴正方形的面积=5×5=25，
∵△AEB的面积=AE×BE=×3×4=6，
∴阴影部分的面积=25-6=19，
故选：C．
本题考查了勾股定理，正方形的面积以及三角形的面积的求法，熟练掌握勾股定理是解题的关键．
5、D
【解析】
由题意可得∠BAE是旋转角为120°且∠BAC=35°，可求∠CAE的度数．
【详解】
∵将△ABC绕点A按顺时针方向旋转120°得到△ADE
∴∠BAE=120°且∠BAC=35°
∴∠CAE=85°
故选D．
本题考查了旋转的性质，关键是熟练运用旋转的性质解决问题．
6、C
【解析】
根据一次函数的图像与直角坐标系坐标特点即可求解.
【详解】
由题意可得，.
∴.
故选C.
此题主要考查一次函数的图像，解题的关键是熟知直角坐标系的特点.
7、D
【解析】
分析：
根据图象中的数据信息进行分析判断即可.
详解：
A选项中，由图象可知：“林老师家距离超市1.5km”，所以A中说法正确；
B选项中，由图象可知：林老师在书店停留的时间为；80-50=30（分钟），所以B中说法正确；
C选项中，由图象可知：林老师从家里到超市的平均速度为：1500÷30=50（米/分钟），林老师从超市到书店的平均速度为：（2000-1500）÷（50-40）=50（米/分钟），所以C中说法正确；
D选项中，由图象可知：林老师从书店到家的平均速度为：2000÷（100-80）=100（米/分钟）=6（千米/时），所以D中说法错误.
故选D.
点睛：读懂题意，“弄清函数图象中每个转折点的坐标的实际意义”是解答本题的关键.
8、A
【解析】
根据题意得，▱ABCD∽▱OECF，且AO=OC=AC，故四边形OECF的面积是▱ABCD面积的．
【详解】
由平移的性质得，▱ABCD∽▱OECF，且AO＝OC＝AC，
故四边形OECF的面积是▱ABCD面积的．，
即图中阴影部分的面积为1cm1．
故选A．
此题主要考查学生对菱形的性质及平移的性质的综合运用．关键是得出四边形OECF的面积是▱ABCD面积的．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
试题解析：∵AD∥BC，
∴∠EDB=∠CBD，又∠EBD=∠CBD，
∴∠EBD=∠EDB，
∴EB=ED，又BC′=BC=AD，
∴EA=EC′，
在Rt△EC′D中，
DE2=EC′2+DC′2，即DE2=（8-DE）2+62，
解得DE=．
10、
【解析】
设直线与x轴交于点C，由直线BC的解析式可得出 结合可得出，通过解含30度角的直角三角形即可得出b值．
【详解】
设直线与x轴交于点C，如图所示:
∵直线BC的解析式为y=x+b，
∴
∵
∴
当x=0时，y=x+b=b.
在Rt△ABO中, OB=b，OA=5，
∴AB=2b，
∴
∴
故答案为：
考查待定系数法求一次函数解析式, 三角形的外角性质, 含角的直角三角形的性质，勾股定理等，综合性比较强，根据直线解析式得到是解题的关键.
11、
【解析】
设正方形OABC的边0A=a，可知OA=OC=AB=CB=a，所以点B的坐标为(aa)，推出反比例函数解析式的k=a，再由CF=2OC-3，可知CF=2a-3，推出点的坐标为( ,3a-3)，根据5CD=3CB，可求出点E的坐标
【详解】
由题意可设：正方形OABC的边OA=a
∴OA= OC=AB= CB
∴点B的坐标为(a,a)，即k=a
CF=2OC-3
∴CF=2a-3
∵OF=OC+CF=a+2a-3=3a-3
∴点E的纵坐标为3a-3
将3a-3代入反比例函数解析式y= 中,可得点E的横坐标为
∵四边形CDEF为矩形,
∴CD=EF=
5CD=3CB
=3a,可求得:a=
将a=,代入点E的坐标为( ,3a-3),
可得:E的坐标为
故答案为：
本题考查了反比例函数图像上点的坐标特征,正方形矩形的性质,熟知在反比例函数的题目中利用设点法找等量关系解方程是解题关键
12、3
【解析】
根据分式的运算法则即可求出答案．
【详解】
解：等式的右边==等式的左边，
∴,
解得：
，
∴A+B=3，
故答案为：3
本题考查分式的运算，解题的关键是熟练掌握分式的运算法则以及二元一次方程组的解法．
13、1
【解析】
过点A作交BC于点E，先根据含1°的直角三角形的性质得出，设，则，根据的面积为27建立方程求出x的值，进而可求出AB,CD的长度，最后利用周长公式求解即可．
【详解】
过点A作交BC于点E，
∵，,
．
∵，
∴设，则．
∵的面积为27，
，
即，
解得或（舍去），
∴，
∴的周长为．
故答案为：1．
本题主要考查含1°的直角三角形的性质及平行四边形的周长和面积，掌握含1°的直角三角形的性质并利用方程的思想是解题的关键．
三、解答题（本大题共5个小题，共48分）
14、（1）甲厂家的总费用：y甲=140x；乙厂家的总费用：当0＜x≤10时，y乙=180x，当x＞10时，y乙=110x+1100；（1）详见解析.
【解析】
（1）根据题目中的数量关系即可得到甲、乙两厂家收取的总费用y（元）与x（米1）之间的函数关系式；
（1）分别画出甲、乙两厂家收取的总费用y（元）与x（米1）的函数图象，结合图象分析即可．
【详解】
解：（1）甲厂家的总费用：y甲=100×0.7x=140x；
乙厂家的总费用：当0＜x≤10时，y乙=100×0.9x=180x，
当x＞10时，y乙=100×0.9×10+100×0.6（x﹣10）
=110x+1100；
（1）甲、乙两厂家收取的总费用y（元）与x（米1）的函数图象如图所示：

若y甲=y乙，140x=110x+1100，x=60，
根据图象，当0＜x＜60时，选择甲厂家；
当x=60时，选择甲、乙厂家都一样；
当x＞60时，选择乙厂家．
本题主要考查了一次函数在实际生活中的应用，涉及到的知识有运用待定系数法求函数的解析式，平面直角坐标系中交点坐标的求法，函数图象的画法等，从图表及图象中获取信息是解题的关键，属于中档题．
15、 (1)∠AFD= 60°（2）DG=CE，DG//CE；（3）详见解析
【解析】
(1) 证明△ABE≌△CAD(SAS)，可得 ∠BAE=∠ACD，继而根据等边三角形的内角为60度以及三角形外角的性质即可求得答案；
(2)由(1)∠AFD=60°，根据∠AEG=60°，可得GE//CD ，继而根据GE=AE=CD，可得四边形GECD是平行四边形，根据平行四边形的性质即可得DG=CE，DG//CE；
(3)延长EA交CD于点F，先证明△ACD≌△BAE，根据全等三角形的性质可得 ∠ACD=∠BAE， CD=AE，继而根据三角形外角的性质可得到∠EFC= 60°，从而得∠EFC=∠GEF，得到GE//CD，继而证明四边形GECD是平行四边形 ，根据平行四边形的性质即可得到DG=CE，DG//CE.
【详解】
(1) ∵△ABC是等边三角形，
∴AB=AC，∠BAC=∠ABC=60°，
在△ABE和△CAD中，
，
∴△ABE≌△CAD(SAS)，
∴∠BAE=∠ACD，
∵∠BAE+∠EAC=∠BAC=60°，
∴∠ACD+∠EAC=60°，
∴∠AFD=∠ACD+∠EAC=60°，
故答案为60° ；
(2)DG=CE，DG//CE，理由如下：
∵△ABC是等边三角形，
∴AB=AC，∠BAC=∠ABC=60°，
在△ABE和△CAD中，
，
∴△ABE≌△CAD(SAS)，
∴AE=CD，∠BAE=∠ACD，
∵∠BAE+∠EAC=∠BAC=60°，
∴∠ACD+∠EAC=60°，
∴∠AFD=∠ACD+∠EAC=60°，
又∵∠AEG=60°，
∴∠AFD=∠AEG，
∴GE//CD ，
∵GE=AE=CD，
∴四边形GECD是平行四边形，
∴DG=CE，DG//CE；
(3)仍然成立
延长EA交CD于点F，
∵△ABC为等边三角形，
∴AC=AB，∠BAC=∠ABC=60°，
∴∠DAC=∠ABE=120°，
在△ACD和△BAE中，
，
∴△ACD≌△BAE(SAS)，
∴∠ACD=∠BAE， CD=AE，
∴∠EFC=∠DAF+∠BDC=∠BAE +∠AEB=∠ABC= 60°，
∴∠EFC=∠GEF，
∴GE//CD，
∵GE=AE=CD，
∴四边形GECD是平行四边形 ，
∴DG=CE，DG//CE.
本题考查了等边三角形的性质，平行四边形的判定与性质，全等三角形的判定与性质，熟练掌握相关知识是解题的关键.注意数形结合思想的运用.
16、（1）见解析；（2）S△ABC＝18.
【解析】
（1）易知AE＝AB，DF＝CD，即可得到AE＝DF，又有AB∥CD，所以四边形AEFD是平行四边形；（2）作CH⊥AB于H．利用平行四边形性质求出∠B，再利用三角函数求出CH，接着利用三角形面积公式求解即可
【详解】
（1）证明：如图．
∵四边形ABCD是平行四边形，
∴AB∥CD且AB＝CD，
∵点E，F分别是AB，CD的中点，
∴AE＝AB，DF＝CD．
∴AE＝DF，
∴四边形AEFD是平行四边形；
（2）如图，作CH⊥AB于H．
∵四边形ABCD是平行四边形，
∴AD＝BC＝6，AD∥BC，
∴∠B＝180°﹣∠DAB＝60°，
∴CH＝BC•sin60°＝3，
∴S△ABC＝•AB•CH＝×12×3＝18
本题主要考查平行四边形的证明与性质，三角函数的简单应用，三角形面积计算等知识点，本题第二问关键在于能够做出辅助线同时利用三角函数求出高
17、（1）；（2）的面积为2；（3）符合条件的点共有3个：，，
【解析】
（1）直线l1交于点D，且点D的纵坐标为4，则4=2x+2，解得：x=1，故点D（1，4），即可求解；
（2）将点B、D的坐标代入y=kx+b，即可求解；
（3）分AB是平行四边形的一条边、AB是平行四边形的对角线两种情况，分别求解．
【详解】
（1）把代入得：
当时，
不等式的解集是
（2）把、代入得：
直线的解析式是：
令
由知：
的面积为2
（3），，
以、、、为顶点的四边形是平行四边形
由平移可知：，，
符合条件的点共有3个：，，
本题为一次函数综合运用题，涉及到平行四边形的基本性质、求解不等式等知识点，其中（3），要注意分类求解，避免遗漏．
18、（1）答案见解析；（2）答案见解析．
【解析】
（1）分别作出点A、B、C向右平移5个方格所得对应点，再顺次连接可得；
（2）分别作出点A、C绕点B顺时针方向旋转所得对应点，再顺次连接可得．
【详解】
解：如图所示，（1）即为平移后的图形；
（2）即为旋转后的图形．
本题主要考查作图旋转变换、平移变换，解题的关键是根据旋转变换和平移变换的定义作出变换后的对应点．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1．
【解析】
解：由图可知，把数据从小到大排列的顺序是：180、182、1、185、186，中位数是1．
故答案为1．
本题考查折线统计图；中位数．
20、1
【解析】
观察图形发现：第1幅图中有1个正方形，第2幅图中有1+4=5个正方形，第3幅图中有1+4+9=14个正方形，…由此得出第n幅图中有12+22+32+42+…+n2＝n（n+1）（2n+1）个正方形从而得到答案．
【详解】
解：∵第1幅图中有1个正方形，
第2幅图中有1+4＝5个正方形，
第3幅图中有1+4+9＝14个正方形，
…
∴第n幅图中有12+22+32+42+…+n2＝n（n+1）（2n+1），
∴第4幅图中有12+22+32+42＝1个正方形．
故答案为1．
此题考查图形的变化规律，利用图形之间的联系，得出数字的运算规律解决问题．
21、4
【解析】
由平行四边形的性质得出AB＝CD＝6，AD∥BC，得出∠DAE＝∠BEA，证出∠BEA＝∠BAE，得出BE＝AB，即可得出CE的长．
【详解】
解：∵四边形ABCD是平行四边形，
∴AB＝CD＝6，AD∥BC，
∴∠DAE＝∠BEA，
∵AE平分∠BAD，
∴∠BAE＝∠DAE，
∴∠BEA＝∠BAE，
∴BE＝AB＝6，
∴CE＝BC−BE＝10−6＝4；
故答案为：4
本题考查了平行四边形的性质、等腰三角形的判定；熟练掌握平行四边形的性质，并能进行推理计算是解决问题的关键．
22、5000(1﹣x)2＝1
【解析】
根据现在售价5000元月平均下降率现在价格1元，即可列出方程．
【详解】
解：设平均每次降价的百分率为x，根据题意可列方程：
5000(1﹣x)2＝1．
故答案为：5000(1﹣x)2＝1．
此题主要考查了由实际问题抽象出一元二次方程，关键是掌握增长率问题的计算公式：变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为．
23、（2，1）
【解析】
平面直角坐标系中任意一点P（x，y），关于x轴的对称点的坐标是（x，﹣y），即关于横轴的对称点，横坐标不变，纵坐标变成相反数，这样就可以求出对称点的坐标．
【详解】
点P（2，﹣1）关于x轴的对称点的坐标是（2，1），
故答案为：2，1．
本题主要考查了平面直角坐标系关于坐标轴成轴对称的两点的坐标之间的关系，是需要识记的内容，比较简单．
二、解答题（本大题共3个小题，共30分）
24、x；2019.
【解析】
直接将括号里面通分运算，再利用分式的混合运算法则化简得出答案.
【详解】
原式
，
当时，原式．
此题主要考查了分式的化简求值，正确化简分式是解题关键.
25、 (1); (2)
【解析】
（1）如图（1），设CE＝x，则BE＝8﹣x；根据勾股定理列出关于x的方程，解方程即可解决问题．
（2）如图（2），首先求出CB′＝3；类比（1）中的解法，设出未知数，列出方程即可解决问题．
【详解】
（1）如图（1），设CE＝x，则BE＝8﹣x；
由题意得：AE＝BE＝8﹣x，
由勾股定理得：x2+62＝（8﹣x）2，
解得：x＝，
即CE的长为：．
（2）如图（2），
∵点B′落在AC的中点，
∴CB′＝AC＝3；
设CE＝x，类比（1）中的解法，可列出方程：x2+32＝（8﹣x）2
解得：x＝．
即CE的长为：．
该题主要考查了翻折变换的性质及其应用问题；解题的关键是灵活运用翻折变换的性质，找出图形中隐含的等量关系；借助勾股定理等几何知识点来分析、判断、推理或解答．
26、（1）见解析；（2）127°；（3）见解析.
【解析】
（1）直接利用轴对称图形的性质得出对应点位置进而得出答案；
（2）利用翻折变换的性质结合平行线的性质得出∠1度数进而得出答案；
（3）利用翻折变换的性质结合勾股定理得出答案．
【详解】
（1）如图所示：
（2）∵∠FDC=16°，
∴∠DFC=74°，
由对称性得，∠1=∠2=
∵AD∥BC，
∴∠AEF=∠GEF=180°-53°=127°；
故答案为：127°．
（3）思路：
a．连接BD交EF于点O．
b．在Rt△DFC中，设FC=x，则FD=4-x，由勾股定理，求得FD长；
c．Rt△BDC中，勾股可得BD=5，由点B与点D的对称性可得OD的长；
d．在Rt△DFO中，同理可求OF的长，可证EF=2OF，求得EF的长．
此题主要考查了翻折变换以及矩形的性质，正确掌握翻折变换的性质是解题关键．
题号
一
二
三
四
五
总分
得分