2025届新疆伊犁州名校九年级数学第一学期开学预测试题【含答案】

这是一份2025届新疆伊犁州名校九年级数学第一学期开学预测试题【含答案】，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）某校规定学生的学期数学成绩由研究性学习成绩与期末卷面成绩共同确定，其中研究性学习成绩占40%，期末卷面成绩占60%，小明研究性学习成绩为80分，期末卷面成绩为90分，则小明的学期数学成绩是（ ）
A．80分B．82分C．84分D．86分
2、（4分）已知a为整数，且＜＜，则a等于（）
A．1B．2C．3D．4
3、（4分）下列图形中，既是轴对称图形又是中心对称图形的是
A．B．C．D．
4、（4分）如图，EF为△ABC的中位线，若AB=6，则EF的长为（ ）
A．2B．3C．4D．5
5、（4分）下列命题中：①两直角边对应相等的两个直角三角形全等；②两锐角对应相等的两个直角三角形全等；③斜边和一直角边对应相等的两个直角三角形全等；④一锐角和斜边对应相等的两个直角三角形全等；⑤一锐角和一边对应相等的两个直角三角形全等．其中正确的个数有（ ）
A．2个B．3个C．4个D．5个
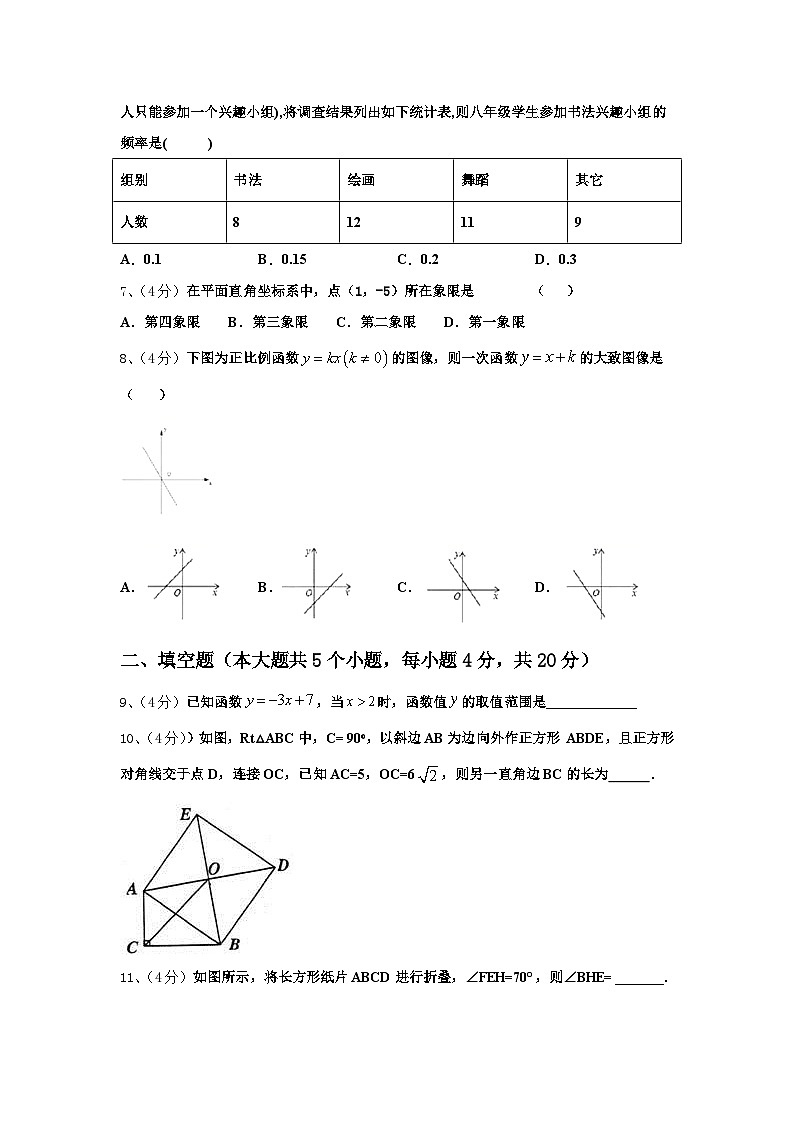
6、（4分）学校为了了解八年级学生参加课外活动兴趣小组的情况,随机抽查了40名学生(每人只能参加一个兴趣小组),将调查结果列出如下统计表,则八年级学生参加书法兴趣小组的频率是( )
A．0.1B．0.15C．0.2D．0.3
7、（4分）在平面直角坐标系中，点（1，-5）所在象限是 （ ）
A．第四象限 B．第三象限 C．第二象限 D．第一象限
8、（4分）下图为正比例函数的图像，则一次函数的大致图像是（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）已知函数，当时，函数值的取值范围是_____________
10、（4分））如图，Rt△ABC中，C= 90，以斜边AB为边向外作正方形 ABDE，且正方形对角线交于点D，连接OC，已知AC=5，OC=6，则另一直角边BC的长为 ．
11、（4分）如图所示，将长方形纸片ABCD进行折叠，∠FEH=70°，则∠BHE=_______.
12、（4分）如图，点是矩形的对角线上一点，过点作，分别交、于、，连接、.若，.则图中阴影部分的面积为____________.
13、（4分）计算：__．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在△ABC 中，∠B=30°，∠C=45°，AC=2．求 BC 边上的高及△ABC 的面积．
15、（8分）直线过点，直线过点，求不等式的解集.
16、（8分）丽君花卉基地出售两种盆栽花卉：太阳花6元/盆，绣球花10元/盆．若次购买的绣球花超过20盆时，超过20盆部分的绣球花价格打8折．
（1）求出太阳花的付款金额（元）关于购买量（盆）的函数关系式；
（2）求出绣球花的付款金额（元）关于购买量（盆）的函数关系式；
（3）为了美化环境，花园小区计划到该基地购买这两种花卉共90盆，其中太阳花数量不超过绣球花数量的一半．两种花卉各买多少盆时，总费用最少，最少费用是多少元？
17、（10分）如图，铁路上A、B两点相距25km，C、D为两村庄，DA⊥AB于A，CB⊥AB于B，已知DA=15km，CB=10km，现在要在铁路AB上建一个土特产品收购站E，使得C、D两村到E站的距离相等，则E站应建在距A站多少千米处？
18、（10分）计算：2b﹣（4a+）（a＞0，b＞0）．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）若b为常数，且﹣bx+1是完全平方式，那么b＝_____．
20、（4分）已知，化简二次根式的正确结果是_______________．
21、（4分）已知在同一坐标系中，某正比例函数与某反比例函数的图像交于 A，B 两点，若点 A 的坐标为（-1,4）， 则点 B 的坐标为___.
22、（4分）△ABC 中，已知：∠C＝90°，AB＝17，BC＝8，则 AC＝_____．
23、（4分）正五边形的内角和等于______度．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，矩形OABC中，点A在x轴上，点C在y轴上，点B的坐标是，矩形OABC沿直线BD折叠，使得点C落在对角线OB上的点E处，折痕与OC交于点D．
（1）求直线OB的解析式及线段OE的长；
（2）求直线BD的解析式及点E的坐标；
（3）若点P是平面内任意一点，点M是直线BD上的一个动点，过点M作轴，垂足为点N，在点M的运动过程中是否存在以P、N、E、O为顶点的四边形是菱形？若存在，直接写出点M的坐标；若不存在，请说明理由．
25、（10分）计算：
（1）-2
（2）（-）•（+）
26、（12分）如图，，是四边形的对角线上两点，，，．求证：四边形是平行四边形．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
利用加权平均数的计算方法直接计算即可得出答案．
【详解】
解：根据题意得：
＝86（分），
答：小明的学期数学成绩是86分；
故选：D．
本题考查加权平均数，解题的关键是掌握加权平均数的计算方法.
2、D
【解析】
根据实数的估算即可求解.
【详解】
∵＜＜，=4
∴a=4
故选D.
此题主要考查实数的估算，解题的关键是熟知实数的性质.
3、D
【解析】
根据轴对称图形和中心对称图形的定义逐项识别即可，在平面内，把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形.
【详解】
解：A. 是轴对称图形，但不是中心对称图形，故不符合题意；
B. 不是轴对称图形，是中心对称图形，故不符合题意；
C. 是轴对称图形，但不是中心对称图形，故不符合题意；
D. 既是轴对称图形又是中心对称图形，故符合题意．
故选D.
本题考查了轴对称图形和中心对称图形的识别，熟练掌握轴对称图形和中心对称图形的定义是解答本题的关键.
4、B
【解析】
根据三角形的中位线的性质即可得到结论．
【详解】
∵EF为△ABC的中位线，若AB=6，
∴EF=AB=3，
故选B．
本题考查了三角形的中位线的性质，熟练掌握三角形中位线定理是解题的关键．
5、C
【解析】
根据全等三角形的判定定理逐项分析，作出判断即可．
【详解】
解：①两直角边对应相等，两直角相等，所以根据SAS可以判定两直角边对应相等的两个直角三角形全等．故①正确；
②两锐角对应相等的两个直角三角形不一定全等，因为对应边不一定相等．故②错误；
③斜边和一直角边对应相等的两个直角三角形，可以根据HL判定它们全等．故③正确；
④一锐角和斜边对应相等的两个直角三角形，可以根据AAS判定它们全等．故④正确；
⑤一锐角和一边对应相等的两个直角三角形，可以根据AAS或ASA判定它们全等．故⑤正确．
综上所述，正确的说法有4个．
故选：C．
本题考查了直角三角形全等的判定．直角三角形首先是三角形，所以一般三角形全等的判定方法都适合它，同时，直角三角形又是特殊的三角形，有它的特殊性，作为“HL”公理就是直角三角形独有的判定方法．所以直角三角形的判定方法最多，使用时应该抓住“直角”这个隐含的已知条件．
6、C
【解析】
根据频率=频数数据总和即可得出答案．
【详解】
解：40人中参加书法兴趣小组的频数是8，
频率是8÷40=0.2，可以用此频率去估计八年级学生参加舒服兴趣小组的频率.
故选：C．
本题是对频率、频数灵活运用的综合考查．注意：每个小组的频数等于数据总数减去其余小组的频数，即各小组频数之和等于数据总和，频率=频数数据总和．
7、A
【解析】分析：根据象限内点的坐标特征即可解答.
详解：点（1，-5）横坐标为正，纵坐标为负，故该点在第四象限.
点睛：本题主要考查了象限内点的坐标特征，牢记点的坐标特征是解题的关键.
8、B
【解析】
根据正比例函数图象所经过的象限，得出k<0，由此可推知一次函数象与y轴交于负半轴且经过一、三象限.
【详解】
解：∵正比例函数y=kx(k≠0)的图象经过二、四象限，
∴k<0，
∴一次函数y=x+k的图象与y轴交于负半轴且经过一、三象限.
故选B.
本题考查了一次函数图象与比例系数的关系.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
依据k的值得到一次函数的增减性，然后结合自变量的取值范围，得到函数值的取值范围即可．
【详解】
∵函数y＝−3x＋7中，k＝−3＜0，
∴y随着x的增大而减小，
当x＝2时，y＝−3×2＋7＝1，
∴当x＞2时，y＜1，
故答案为：y＜1．
本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y＝ax＋b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y＝kx＋b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
10、4．
【解析】
正方形的性质，全等三角形的判定和性质，矩形的判定和性质，等腰直角三角形的判定和性质，勾股定理．
【分析】如图，过O作OF垂直于BC，再过O作OF⊥BC，过A作AM⊥OF，
∵四边形ABDE为正方形，∴∠AOB=90°，OA=OB．
∴∠AOM+∠BOF=90°．
又∵∠AMO=90°，∴∠AOM+∠OAM=90°．∴∠BOF=∠OAM．
在△AOM和△BOF中，
∵∠AMO=∠OFB=90°，∠OAM=∠BOF， OA=OB，
∴△AOM≌△BOF（AAS）．∴AM=OF，OM=FB．
又∵∠ACB=∠AMF=∠CFM=90°，∴四边形ACFM为矩形．∴AM=CF，AC=MF=2．
∴OF=CF．∴△OCF为等腰直角三角形．
∵OC=3，∴根据勾股定理得：CF2+OF2=OC2，即2CF2=（3）2，解得：CF=OF=3．
∴FB=OM=OF－FM=3－2=4．∴BC=CF+BF=3+4=4．
11、70°
【解析】
由折叠的性质可得∠DEH=∠FEH=70°，再根据两直线平行，内错角相等即可求得答案.
【详解】
由题意得∠DEH=∠FEH=70°，
∵AD//BC，
∴∠BHE=∠DEH=70°，
故答案为：70°.
本题考查了折叠的性质，平行线的性质，熟练掌握折叠的性质以及平行线的性质是解题的关键.
12、
【解析】
由矩形的性质可证明S△DFP＝S△PBE，即可求解．
【详解】
解：作PM⊥AD于M，交BC于N．
则有四边形AEPM，四边形DFPM，四边形CFPN，四边形BEPN都是矩形，
∴S△ADC＝S△ABC，S△AMP＝S△AEP，S△PBE＝S△PBN，S△PFD＝S△PDM，S△PFC＝S△PCN，
∴S△DFP＝S△PBE＝×2×5＝5，
∴S阴＝5＋5＝10，
故答案为：10.
本题考查矩形的性质、三角形的面积等知识，解题的关键是证明S△DFP＝S△PBE．
13、-
【解析】
直接利用二次根式的性质分别计算得出答案．
【详解】
解：原式
．
故答案为：．
此题主要考查了二次根式的加减运算，正确化简二次根式是解题关键．
三、解答题（本大题共5个小题，共48分）
14、2，2+2.
【解析】
先根据AD⊥BC，∠C=45°得出△ACD是等腰直角三角形，再由AC=2 得出AD及CD的长，由∠B=30°求出BD的长，根据三角形的面积公式即可得出结论．
【详解】
∵AD⊥BC,∠C=45°，
∴△ACD是等腰直角三角形，
∵AD=CD.
∵AC=2，
∴2AD=AC,即2AD=8，解得AD=CD=2.
∵∠B=30°，
∴AB=2AD=4，
∴BD= ，
∴BC=BD+CD=2 +2，
∴S = BC⋅AD= (2+2)×2=2+2.
此题考查勾股定理，解题关键在于求出BD的长.
15、
【解析】
将代入，可解得k的值，将代入，可解得m的值，再将k和m的值代入不等式，解不等式即可
【详解】
解：将代入得：，解得：k=1；
将代入得：，解得：；
∴，
则可得
解得
故答案为：
本题考查待定系数法求一次函数的解析式以及不等式的解法，，比较简单，应熟练掌握
16、（1）：y1=6x；（2）y2=；（3）太阳花30盆，绣球花60盆时，总费用最少，最少费用是700元
【解析】
（1）根据总价=单价×数量，求出太阳花的付款金额y1（元）关于购买量x（盆）的函数解析式；
（2分两种情况：①一次购买的绣球花不超过20盆；②一次购买的绣球花超过20盆；根据总价=单价×数量，求出绣球花的付款金额y2（元）关于购买量x（盆）的函数解析式即可；
（3）首先太阳花数量不超过绣球花数量的一半，可得太阳花数量不超过两种花数量的，即太阳花数量不超过30盆，所以绣球花的数量不少于60盆；然后设太阳花的数量是x盆，则绣球花的数量是90-x盆，根据总价=单价×数量，求出购买两种花的总费用是多少，进而判断出两种花卉各买多少盆时，总费用最少，最少费用是多少元即可．
【详解】
解：（1）太阳花的付款金额y1（元）关于购买量x（盆）的函数解析式是：y1=6x；
（2）①一次购买的绣球花不超过20盆时，
付款金额y2（元）关于购买量x（盆）的函数解析式是：y2=10x（x≤20）；
②一次购买的绣球花超过20盆时，
付款金额y2（元）关于购买量x（盆）的函数解析式是：
y2=10×20+10×0.8×(x-20)
=200+8x-160
=8x+40
综上，可得
绣球花的付款金额y2（元）关于购买量x（盆）的函数解析式是：
y2=
（3）根据题意，可得太阳花数量不超过：90×（盆），
所以绣球花的数量不少于：90-30=60（盆），
设太阳花的数量是x盆，则绣球花的数量是(90-x)盆，购买两种花的总费用是y元，
则x≤30，
则y=6x+[8(90-x)+40]
=6x+[760-8x]
=760-2x，
∵-2＜0，
∴y随x的增大而减小，
∵x≤30，
∴当x=30时，
y最小=760-2×30=700（元），
90-30=60盆，
答：太阳花30盆，绣球花60盆时，总费用最少，最少费用是700元．
本题主要考查了一次函数的应用，要熟练掌握，解答此题的关键是要明确：分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符合实际．此题还考查了单价、总价、数量的关系：总价=单价×数量，单价=总价÷数量，数量=总价÷单价，要熟练掌握．
17、E点应建在距A站1千米处．
【解析】
关键描述语：产品收购站E，使得C、D两村到E站的距离相等，在Rt△DAE和Rt△CBE中，设出AE的长，可将DE和CE的长表示出来，列出等式进行求解即可．
【详解】
解：设AE＝xkm，
∵C、D两村到E站的距离相等，∴DE＝CE，即DE2＝CE2，
由勾股定理，得152+x2＝12+（25﹣x）2，x＝1．
故：E点应建在距A站1千米处．
本题主要是运用勾股定理将两个直角三角形的斜边表示出来，两边相等求解即可．
18、﹣5．
【解析】
分析：
按照二次根式的相关运算法则进行化简计算即可.
详解：
原式=2b×﹣4a×﹣3
=2﹣4﹣3
=﹣5．
点睛：熟记“二次根式的相关运算性质、法则”是正确解答本题的关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、±1
【解析】
根据完全平方式的一般式，计算一次项系数即可.
【详解】
解：∵b为常数，且x2﹣bx+1是完全平方式，
∴b＝±1，
故答案为±1．
本题主要考查完全平方公式的系数关系，关键在于一次项系数的计算.
20、
【解析】
由题意：-a3b≥0，即ab≤0，
∵a＜b，
∴a≤0＜b；
所以原式=|a|=-a．
21、 (1,−4)
【解析】
根据反比例函数图象上点的坐标特征，正比例函数与反比例函数的两交点坐标关于原点对称．
【详解】
∵反比例函数是中心对称图形，正比例函数与反比例函数的图象的两个交点关于原点对称，
∵一个交点的坐标为(−1,4)，
∴它的另一个交点的坐标是(1,−4)，
故答案为：(1,−4).
本题考查反比例函数图象的对称性，解题的关键是掌握反比例函数图象的对称性.
22、15
【解析】
根据勾股定理即可算出结果.
【详解】
在△ABC中，∠C=90°，AB=17，BC=8，
所以AC=
故答案为：15
本题考查了勾股定理，掌握勾股定理：在直角三角形中两条直角边的平方和等于斜边的平方，是解题的关键．
23、540
【解析】
过正五边形五个顶点，可以画三条对角线，把五边形分成3个三角形
∴正五边形的内角和=3180=540°
二、解答题（本大题共3个小题，共30分）
24、（1），OE=4；（2），；（3）存在，点M的坐标为或或或
【解析】
利用待定系数法求出k，再利用勾股定理求出OB，由折叠求出，即可得出结论；
利用勾股定理求出点D坐标，利用待定系数法求出直线BD的解析式，最后用三角形的面积公式求出点E的横坐标，即可得出结论；
分两种情况，利用菱形的性质求出点N坐标，进而得出点M的横坐标，代入直线BD解析式中，即可得出结论．
【详解】
解：设直线OB的解析式为，
将点代入中，得，
，
直线OB的解析式为，
四边形OABC是矩形，且，
，，
，，
根据勾股定理得，，
由折叠知，，
；
设，
，
由折叠知，，，
在中，，
根据勾股定理得，，
，
，
，，
设直线BD的解析式为 ，
，
∴6k`+5=8
∴K`=
直线BD的解析式为，
由知，直线OB的解析式为，
设点，
根据的面积得，，
，
；
由知，，
以P、N、E、O为顶点的四边形是菱形，
当OE是菱形的边时，，
或，
Ⅰ、当时，
轴，
点M的横坐标为4，
点M是直线BD：上，
，
Ⅱ、当时，
轴，
点M的横坐标为，
点M是直线BD：上，
，
当OE是菱形的对角线时，记对角线的交点为，，
由知，，
，
由知，直线OB的解析式为，
点过直线PN，
直线PN的解析式为，
令，
，
，
，
轴，
点M的横坐标为，
点M是直线BD：上，
，
当ON为对角线时，ON与EP互相平分，
点，
；
即：点M的坐标为或或或
此题是一次函数综合题，主要考查了矩形的性质，菱形的性质，待定系数法，三角形的面积公式，勾股定理，求出点D坐标是解本题的关键．
25、（1）；（2）﹣1．
【解析】
(1)先把二次根式化为最简二次根式，然后合并即可；
(2)利用平方差公式进行计算即可．
【详解】
(1)原式
=2
；
(2)原式=2﹣5
=﹣1．
本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可.在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．
26、见解析
【解析】
由平行线的性质得出∠AEB=∠CFD，求出BE=DF，由SAS即可得出△ABE≌△CDF，可得∠ABD=∠CDB，AB=CD，从而可判定四边形ABCD是平行四边形.
【详解】
解：证明：∵AE∥CF，
∴∠AEB=∠CFD，
∵BF=DE，
∴BF+EF=DE+EF，即BE=DF，
在△ABE和△CDF中，
，
∴△ABE≌△CDF（SAS），
∴∠ABD=∠CDB，AB=CD，
∴AB∥CD，
∴四边形ABCD是平行四边形．
本题考查了全等三角形的判定和性质、平行线的性质、平行四边形的判定；熟练掌握全等三角形的判定方法是解题的关键．
题号
一
二
三
四
五
总分
得分
组别
书法
绘画
舞蹈
其它
人数
8
12
11
9