天津经济技术开发区国际学校2024-2025学年九年级上学期第一次月考数学试题(无答案)

这是一份天津经济技术开发区国际学校2024-2025学年九年级上学期第一次月考数学试题(无答案)，共5页。试卷主要包含了本卷共12题，共36分，若，是方程的两个根，则，已知抛物线，下列说法正确的是等内容，欢迎下载使用。

命题人：曾晓英 审卷人：王梓懿
本试卷分为第Ⅰ卷（选择题）、第Ⅱ卷（非选择题）两部分。第Ⅰ卷为第Ⅰ页至第3页，第Ⅱ卷为第4页至第6页。试卷满分120分。考试时间100分钟。
答卷前，考生务必将自己的姓名、考生号、考场号、座位号填写在“答题卡”上。答题时，务必将答案涂写在、“答题卡”上，答案答在试卷上无效。考试结束后，将本试卷和“答题卡”一并交回。
祝各位考生考试顺利！
第Ⅰ卷
注意事项：
1．每题选出答案后，用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点。
2．本卷共12题，共36分。
一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1．下列方程中，属于一元二次方程的是（ ）
A．B．C．D．
2．方程的一次项系数和常数项分别是（ ）
A．2，15B．-6，15C．6，-15D．-6，-15
3．用配方法解方程，变形后的结果正确的是（ ）
A．B．C．D．
4．若，是方程的两个根，则（ ）
A．B．C．D．
5．将抛物线向左平移Ⅰ个单位长度，再向下平移2个单位长度，所得到的抛物线为（ ）
A．B．
C．D．
6．已知抛物线，下列说法正确的是（ ）
A．开口向上B．对称轴是直线
C．顶点坐标为D．当时，y随x的增大而减小
7．2024年是中国共产党建党103周年，全国各地积极开展“弘扬红色文化，重走长征路”主题教育活动．据了解，某展览中心3月份的参观人数为10万人，5月份的参观人数增加到12.1万人．设参观人数的月平均增长率为x，则可列方程为（ ）
A．B．
C．D．
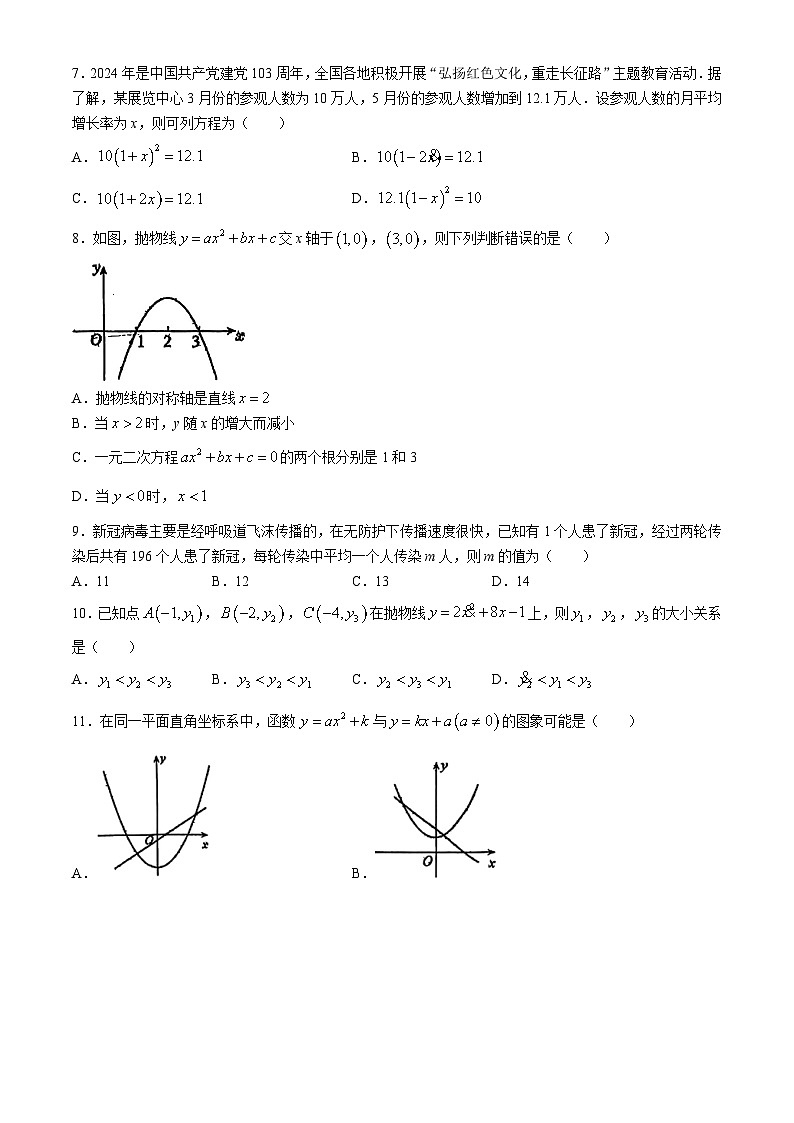
8．如图，抛物线交x轴于，，则下列判断错误的是（ ）
A．抛物线的对称轴是直线
B．当时，y随x的增大而减小
C．一元二次方程的两个根分别是1和3
D．当时，
9．新冠病毒主要是经呼吸道飞沫传播的，在无防护下传播速度很快，已知有1个人患了新冠，经过两轮传染后共有196个人患了新冠，每轮传染中平均一个人传染m人，则m的值为（ ）
A．11B．12C．13D．14
10．已知点，，在抛物线上，则，，的大小关系是（ ）
A．B．C．D．
11．在同一平面直角坐标系中，函数与的图象可能是（ ）
A．B．
C．D．
12．如图，要围一个矩形菜园ABCD，其中一边AD是墙，且AD的长不能超过26m，其余的三边AB，BC，CD用篱笆，且这三边的和为40m，有下列结论：①AB的长可以为6m；②AB的长有两个不同的值满足菜园ABCD面积为192m2；③菜园ABCD面积的最大值为210m2．其中正确结论的个数是（ ）
A．0B．1C．2D．3
第Ⅱ卷
注意事项：
1．用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。
2．本卷共13题，共84分。
二、填空题（本大题共6小题，每小题3分，共18分）
13．若函数是二次函数，则m的值为______．
14．已知二次函数有最小值，则a的取值范围是______．
15．二次函数图象的顶点坐标为______．
16．如图，在期末体育测试中，小朱掷出的实心球的飞行高度y（米）与水平距离x（米）之间的关系大致满足二次函数，则小朱本次投掷实心球的成绩为______m．
（第16题图）
17．一商店销售某种商品，平均每天可售出20件，每件盈利40元．为了扩大销售、增加盈利，该店采取了降价措施，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件．当每件商品降价多少元时，该商店每天销售利润为1200元？若设降价x元，可列方程______。
18．已知二次函数的图象如下，在第三象限内的抛物线上有一动点P，过点P作轴，垂足为N，连接BC交PN于点Q，则的最大值是______．
（第18题图）
三、解答题（本大题共7小题，共66分．解答应写出文字说明、演算步骤或推理过程）
19．（本小题8分）
解下列一元二次方程：
①；②；③；④．
20．（本小题8分）
已知关于x的方程．
（Ⅰ）若方程有一个根为2，求a的值及该方程的另一个根；
（Ⅱ）求证：不论a取任何实数，该方程都有两个不相等的实数根．
21．（本小题10分）
我们已经历了“一次函数”的学习过程，请你根据已有的经验和方法尝试完成下列问题：已知，二次函数中的x和y满足如下表：
（Ⅰ）可求得m的值为______；n的值为______；这个函数的对称轴是______；
（Ⅱ）求出这个二次函数的解析式；
（Ⅲ）当时，则y的取值范围为______．
22．（本小题10分）
如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m．
（Ⅰ）若以拱顶点N为原点建立平面直角坐标系（如右图），则A点坐标是______，B点坐标是______；
（Ⅱ）根据（Ⅰ）所建立的平面直角坐标系，求出抛物线的解析式；
（Ⅲ）因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．
23．（本小题10分）
某商店经销一种健身球，已知这种健身球的成本价为每个20元，市场调查发现，该种健身球每天的销售量y（个）与销售单价x（元）有如下关系：，设这种健身球每天的销售利润为w元（Ⅰ）如果销售单价定为25元，那么健身球每天的销售量是______个；
（Ⅱ）求w与x之间的函数关系式；
（Ⅲ）该种健身球销售单价定为多少元时，每天的销售利润最大?最大利润是多少元?
24．（本小题10分）
一块三角形材料如图所示，，，，用这块材料剪出一个矩形CDEF，其中D、E、F分别在BC、AB、AC上．
（Ⅰ）若设，则______；（用含x的代数式表示）
（Ⅱ）要使剪出的矩形CDEF的面积最大，点E应选在何处？
25．（本小题10分）
如图，抛物线与x轴交于A，B两点，与y轴交于点C．已知点A的坐标是，抛物线的对称轴是直线．
（Ⅰ）求函数解析式和点B的坐标；
（Ⅱ）在对称轴上找一点P，使的值最小．求点P的坐标和的最小值；
（Ⅲ）第一象限内的抛物线上有一动点M，连接MC、MB，求面积的最大值，以及取得最大值时点M的坐标．…
0
1
2
3
4
5
…
…
3
0
-1
0
m
n
…