

所属成套资源:苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)(专项拔高卷)特训(学生版+解析)
- 苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)专题6.1线段、射线、直线(专项拔高卷)特训(学生版+解析) 试卷 1 次下载
- 苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)专题6.2角(专项拔高卷)特训(学生版+解析) 试卷 1 次下载
- 苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)期末压轴题型专练(填空题35题)(特训(学生版+解析)) 试卷 2 次下载
- 苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)期末压轴题型专练(解答题30题)(特训(学生版+解析)) 试卷 1 次下载
- 苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)期末压轴题型专练(选择题35题)(特训(学生版+解析)) 试卷 1 次下载
苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)专题6.3相交线与平行线(专项拔高卷)特训(学生版+解析)
展开
这是一份苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)专题6.3相交线与平行线(专项拔高卷)特训(学生版+解析),共27页。试卷主要包含了3 相交线与平行线,57,5°C.25°D.67,8 °.等内容,欢迎下载使用。
考试时间:90分钟 试卷满分:100分 难度:0.57
姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2022秋•亭湖区期末)如图,把一个圆剪去一部分,所得涂色部分的图形周长比原来圆的周长小,能正确解释这一现象的数学知识是( )
A.垂线段最短B.两点确定一条直线
C.两点之间,线段最短D.经过一点有无数条直线
2.(2分)(2019秋•宿城区校级期末)一副三角板按如图所示的方式摆放,且∠1的度数是∠2的3倍,则∠2的度数为( )
A.20°B.22.5°C.25°D.67.5°
3.(2分)(2016秋•太仓市校级期末)如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有( )
A.4个B.3个C.2个D.1个
4.(2分)(2022秋•泗阳县期末)已知∠α=52°,则∠α的余角的度数为( )
A.38°B.48°C.52°D.128°
5.(2分)(2018秋•沭阳县期末)下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行
B.不相交的两条直线叫做平行线
C.两点确定一条直线
D.两点间的距离是指连接两点间的线段
6.(2分)(2016秋•锡山区期末)下列叙述,其中不正确的是( )
A.两点确定一条直线
B.同角(或等角)的余角相等
C.过一点有且只有一条直线与已知直线平行
D.两点之间的所有连线中,线段最短
7.(2分)(2022秋•玄武区校级期末)如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,OF平分∠BOD,若∠AOC+∠DOF=39°,则∠EOF的度数为( )
A.77°B.74°C.67°D.64°
8.(2分)(2018秋•江宁区校级期末)如图,河道l的一侧有A、B两个村庄,现要铺设一条引水管道把河水引向A、B两村,下列四种方案中最节省材料的是( )
A.B.
C.D.
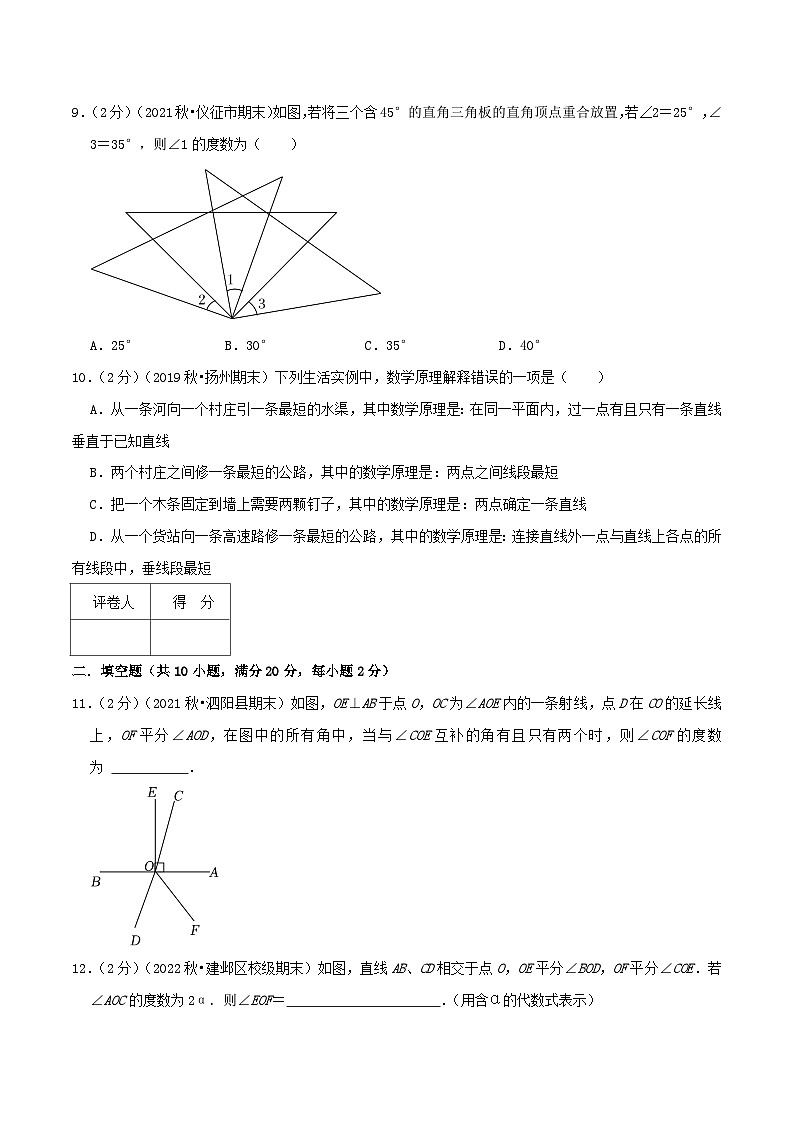
9.(2分)(2021秋•仪征市期末)如图,若将三个含45°的直角三角板的直角顶点重合放置,若∠2=25°,∠3=35°,则∠1的度数为( )
A.25°B.30°C.35°D.40°
10.(2分)(2019秋•扬州期末)下列生活实例中,数学原理解释错误的一项是( )
A.从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线
B.两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短
C.把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线
D.从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2021秋•泗阳县期末)如图,OE⊥AB于点O,OC为∠AOE内的一条射线,点D在CO的延长线上,OF平分∠AOD,在图中的所有角中,当与∠COE互补的角有且只有两个时,则∠COF的度数为 .
12.(2分)(2022秋•建邺区校级期末)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.若∠AOC的度数为2α.则∠EOF= .(用含α的代数式表示)
13.(2分)(2022秋•镇江期末)如图,将一副三角板(三角板AMB和三角板CND)叠在一起,使两个直角顶点M、N重合,若∠AMD=120°,则∠BMC= .
14.(2分)(2022秋•鼓楼区校级期末)如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:
①∠1是∠ACD的余角;
②图中互余的角共有3对;
③∠1的补角只有∠DCF;
④与∠ADC互补的角共有3个.
其中正确结论有 .
15.(2分)(2022秋•仪征市期末)如图,点O在直线AB上,OC⊥OD,若∠COB=60°,则∠AOD的大小为 °.
16.(2分)(2022秋•溧水区期末)如图,OA⊥OB,垂足为O,射线OC在∠AOB的内部,∠AOC<30°,若∠BOD=∠AOC,OE平分∠AOD,设∠EOD=m°,则∠COB= °(用含m的代数式表示).
17.(2分)(2020秋•苏州期末)已知直线AB与直线CD相交于点O,EO⊥CD,垂足为O.若∠AOC=25°12′,则∠BOE的度数为 °.(单位用度表示)
18.(2分)(2022秋•海门市期末)一个角的余角比它的补角的大15°,则这个角的度数是 °.
19.(2分)(2016秋•建湖县期末)下列四种说法:
①过一点有且只有一条直线与已知直线平行;
②在同一平面内,两条不相交的线段是平行线段;
③相等的角是对顶角;
④在同一平面内,若直线AB∥CD,直线AB与EF相交,则CD与EF相交.
其中,错误的是 (填序号).
20.(2分)(2021秋•新吴区期末)如图,将一副三角板的直角顶点O叠放在一起,∠BOC=∠AOD,则∠BOD= °.
三.解答题(共8小题,满分60分)
21.(6分)(2022秋•南通期末)如图,∠AOC与∠BOC互为补角,∠BOC与∠BOD互为余角,且∠BOC=4∠BOD.
(1)求∠BOC的度数;
(2)若OE平分∠AOC,求∠BOE的度数.
22.(6分)(2023春•临清市期中)如图,直线AB,CD相交于点O,OE是∠COB的平分线,FO⊥OE,已知∠AOD=70°.
(1)求∠BOE的度数;
(2)OF平分∠AOC吗?为什么?
23.(8分)(2020秋•淮阴区期末)如图,O为直线AB上一点,DO⊥OE,OC平分∠AOD,∠AOC=24°,求∠BOE的度数.
24.(8分)(2022秋•建邺区校级期末)如图.
(1)∠AOB的余角为∠AOC,射线OM平分∠AOB,当∠AOB=40°,求∠MOC的度数;
(2)若∠AOB的补角为∠BOD,射线ON平分∠BOD,试用含α的代数式表示∠AON的度数.(画出图形,并直接写出结果)
25.(8分)(2022秋•高邮市期末)如图,已知直线AB与CD相交于点O,OE⊥CD于点O、OD是∠BOF的平分线.
(1)若∠BOE=112°,求∠EOF的度数;
(2)∠AOC的补角是 ,∠AOC的余角是 .
26.(8分)(2016秋•江阴市期末)如图,直线AB、CD相交于O,∠2﹣∠1=15°,∠3=130°.
(1)求∠2的度数;
(2)试说明OE平分∠COB.
27.(8分)(2022秋•海门市期末)已知∠AOB=120°,∠COD在∠AOB内部,∠COD=60°.
(1)如图1,若∠BOD=30°,求∠AOC的度数;
(2)如图2,若OE平分∠BOC,请说明:∠AOC=2∠DOE;
(3)如图3,若在∠AOB的外部分别作∠AOC,∠BOD的余角∠AOP,∠BOQ,试探究∠AOP,∠BOQ,∠COD三者之间的数量关系,并说明理由.
28.(8分)(2021秋•苏州期末)如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB(其中∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒.
(1)当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间数量关系为 ;
(2)若射线OC的位置保持不变,且∠COE=130°.
①在旋转的过程中,是否存在某个时刻,使得射线OA,OC,OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意t的值,若不存在,请说明理由;
②如图3,在旋转的过程中,边AB与射线OE相交,请直接写出∠AOC﹣∠BOE的值.
2023-2024学年苏科版数学七年级上册同步专题热点难点专项练习
专题6.3 相交线与平行线(专项拔高卷)
考试时间:90分钟 试卷满分:100分 难度:0.57
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2022秋•亭湖区期末)如图,把一个圆剪去一部分,所得涂色部分的图形周长比原来圆的周长小,能正确解释这一现象的数学知识是( )
A.垂线段最短B.两点确定一条直线
C.两点之间,线段最短D.经过一点有无数条直线
解:由于两点之间线段最短,
∴把一个圆剪去一部分,所得涂色部分的图形周长比原来圆的周长小,
故选:C.
2.(2分)(2019秋•宿城区校级期末)一副三角板按如图所示的方式摆放,且∠1的度数是∠2的3倍,则∠2的度数为( )
A.20°B.22.5°C.25°D.67.5°
解:根据图形得出:∠1+∠2=180°﹣90°=90°,
∵∠1的度数是∠2的3倍,
∴4∠2=90°,
∴∠2=22.5°,
故选:B.
3.(2分)(2016秋•太仓市校级期末)如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有( )
A.4个B.3个C.2个D.1个
解:∵∠α和∠β互补,
∴∠α+∠β=180°.因为90°﹣∠β+∠β=90°,所以①正确;
又∠α﹣90°+∠β=∠α+∠β﹣90°=180°﹣90°=90°,②也正确;
(∠α+∠β)+∠β=×180°+∠β=90°+∠β≠90°,所以③错误;
(∠α﹣∠β)+∠β=(∠α+∠β)=×180°=90°,所以④正确.
综上可知,①②④均正确.
故选:B.
4.(2分)(2022秋•泗阳县期末)已知∠α=52°,则∠α的余角的度数为( )
A.38°B.48°C.52°D.128°
解:∵∠α=52°,
∴∠α的余角=90°﹣52°=38°,
故选:A.
5.(2分)(2018秋•沭阳县期末)下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行
B.不相交的两条直线叫做平行线
C.两点确定一条直线
D.两点间的距离是指连接两点间的线段
解:A、应为过直线外一点有且只有一条直线与已知直线平行,故本选项错误;
B、应为同一平面内,不相交的两条直线叫做平行线,故本选项错误;
C、直线公理:经过两点有且只有一条直线,简称:两点确定一条直线,故本选项正确;
D、应为两点的距离是指连接两点间线段的长度,故本选项错误;
故选:C.
6.(2分)(2016秋•锡山区期末)下列叙述,其中不正确的是( )
A.两点确定一条直线
B.同角(或等角)的余角相等
C.过一点有且只有一条直线与已知直线平行
D.两点之间的所有连线中,线段最短
解:A、两点确定一条直线,故A正确;
B、同角(或等角)的余角相等,故B正确;
C、过直线外一点有且只有一条直线与已知直线平行,故C错误;
D、两点之间的所有连线中,线段最短,故D正确;
故选:C.
7.(2分)(2022秋•玄武区校级期末)如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,OF平分∠BOD,若∠AOC+∠DOF=39°,则∠EOF的度数为( )
A.77°B.74°C.67°D.64°
解:∵EO⊥AB,
∴∠EOB=90°.
∵OF平分∠BOD,
∴∠BOD=2∠BOF=2∠DOF,
∴∠AOC=∠BOD=2∠BOF,
∵∠AOC+∠DOF=39°,
∴3∠BOF=39°.
∵∠BOF=13°,
∴∠EOF=∠BOE﹣∠BOF=90°﹣13°=77°.
故选:A.
8.(2分)(2018秋•江宁区校级期末)如图,河道l的一侧有A、B两个村庄,现要铺设一条引水管道把河水引向A、B两村,下列四种方案中最节省材料的是( )
A.B.
C.D.
解:依据垂线段最短,以及两点之间,线段最短,可得最节省材料的是:
故选:B.
9.(2分)(2021秋•仪征市期末)如图,若将三个含45°的直角三角板的直角顶点重合放置,若∠2=25°,∠3=35°,则∠1的度数为( )
A.25°B.30°C.35°D.40°
解:
∵∠AOB=∠COD=90°
∴∠4=∠AOC=25°,
∴∠1=∠EOF﹣∠2﹣∠DOF=90°﹣25°﹣35°=30°,
故选:B.
10.(2分)(2019秋•扬州期末)下列生活实例中,数学原理解释错误的一项是( )
A.从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线
B.两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短
C.把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线
D.从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短
解:A、从一条河向一个村庄引一条最短的水渠,其中数学原理是:垂线段最短,故原命题错误;
B、两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短,正确;
C、一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线,正确;
D、从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短,正确.
故选:A.
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2021秋•泗阳县期末)如图,OE⊥AB于点O,OC为∠AOE内的一条射线,点D在CO的延长线上,OF平分∠AOD,在图中的所有角中,当与∠COE互补的角有且只有两个时,则∠COF的度数为 120° .
解:∵OF平分∠AOD,
∴∠AOF=∠DOF,
∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∴∠EOC+∠DOE=180°,
∵与∠COE互补的角有且只有两个,
∴∠DOE=∠AOE+∠AOF=∠BOE+∠BOD=180°﹣∠EOC,
即要求∠BOD=∠AOF=∠DOF=60°.
此时∠COF=∠AOC+∠AOF=120°.
故答案为:120°.
12.(2分)(2022秋•建邺区校级期末)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.若∠AOC的度数为2α.则∠EOF= 90°﹣ .(用含α的代数式表示)
解:∵∠AOC=2α,
∴∠BOD=∠AOC=2α,
∵OE平分∠BOD,OF平分∠COE,
∴∠BOE=∠DOE=α,∠COF=∠EOF=∠COE,
∴∠EOC=180°﹣α,
∴∠EOF=90°﹣,
故答案为:90°﹣.
13.(2分)(2022秋•镇江期末)如图,将一副三角板(三角板AMB和三角板CND)叠在一起,使两个直角顶点M、N重合,若∠AMD=120°,则∠BMC= 60° .
解:∵∠AMD=120°,∠AMB=90°,
∴∠BMD=∠AMD﹣∠AMB=30°,
∵∠CMD=90°,
∴∠BMC=∠CMD﹣∠BMD=90°﹣30°=60°,.
故答案为:60°.
14.(2分)(2022秋•鼓楼区校级期末)如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:
①∠1是∠ACD的余角;
②图中互余的角共有3对;
③∠1的补角只有∠DCF;
④与∠ADC互补的角共有3个.
其中正确结论有 ①④ .
解:∵AC⊥BF,
∴∠BCA=90°,
∴∠ACD+∠1=90°,
∴∠1是∠ACD的余角,故①正确;
∵CD⊥BE,
∴∠ADC=∠CDB=90°,
∴∠B+∠BCD=90°,∠ACD+∠DAC=90°,
∵∠BCA=90°,
∴∠B+∠BAC=90°,∠1+∠ACD=90°,
∴图中互余的角共有4对,故②错误;
∵∠1+∠DCF=180°,
∴∠1的补角是∠DCF,
∵∠1+∠DCA=90°,∠DAC+∠DCA=90°,
∴∠1=∠DAC,
∵∠DAC+∠CAE=180°,
∴∠1+∠CAE=180°,
∴∠1的补角有∠CAE,故③说法错误;
∵∠ACB=90°,∠ACF=90°,∠ADC=∠BDC=90°,
∴∠BDC,∠ACB,∠ACF和∠ADC互补,故④说法正确.
正确的是①④;
故答案为:①④.
15.(2分)(2022秋•仪征市期末)如图,点O在直线AB上,OC⊥OD,若∠COB=60°,则∠AOD的大小为 150 °.
解:∵OC⊥OD,
∴∠COD=90°,
∵∠COB=60°,
∴∠DOB=∠DOC﹣∠COB=30°,
∴∠AOD=180°﹣30°=150°,
故答案为:150.
16.(2分)(2022秋•溧水区期末)如图,OA⊥OB,垂足为O,射线OC在∠AOB的内部,∠AOC<30°,若∠BOD=∠AOC,OE平分∠AOD,设∠EOD=m°,则∠COB= 2m或(180﹣2m) °(用含m的代数式表示).
解:当OD在∠AOB内时,如图(1),
∵OE平分∠AOD,
∴∠EOD=∠AOE=m°,
∴∠BOD=∠AOC=90°﹣2m°,
∴∠COB=90°﹣∠AOC=90°﹣(90°﹣2m°)=2m°;
当OD在∠AOB外时,如图(2),
∵OE平分∠AOD,
∴∠EOD=∠AOE=m°,
∴∠AOD=2m°,
∴∠AOC=∠BOD=2m°﹣90°,
∴∠BOC=∠AOB﹣∠AOC=90°﹣(2m°﹣90°)=180°﹣2m°,
∴∠COB=2m°或180°﹣2m°.
故答案为:2m或(180﹣2m).
17.(2分)(2020秋•苏州期末)已知直线AB与直线CD相交于点O,EO⊥CD,垂足为O.若∠AOC=25°12′,则∠BOE的度数为 64.8 °.(单位用度表示)
解:∵EO⊥CD,
∴∠EOD=90°.
∵∠BOD=∠AOC,∠AOC=25°12′,
∴∠BOD=25°12′.
∴∠BOE=∠EOD﹣∠BOD=90°﹣25°12′=64°48′=64.8°.
故答案为64.8.
18.(2分)(2022秋•海门市期末)一个角的余角比它的补角的大15°,则这个角的度数是 40 °.
解:设这个角的度数为x,
根据题意得:90°﹣x=(180°﹣x)+15°,
解得:x=40°.
所以这个角的度数为40°.
故答案为:40.
19.(2分)(2016秋•建湖县期末)下列四种说法:
①过一点有且只有一条直线与已知直线平行;
②在同一平面内,两条不相交的线段是平行线段;
③相等的角是对顶角;
④在同一平面内,若直线AB∥CD,直线AB与EF相交,则CD与EF相交.
其中,错误的是 ①②③ (填序号).
解:∵过直线外一点有且只有一条直线与已知直线平行,∴①错误;
∵在同一平面内,两条不相交的线段可能在一条直线上,说两线段是平行线段不对,∴②错误;
∵相等的角不一定是对顶角,∴③错误;
∵在同一平面内,若直线AB∥CD,直线AB与EF相交,则CD与EF相交,正确,∴④正确;
故答案为:①②③.
20.(2分)(2021秋•新吴区期末)如图,将一副三角板的直角顶点O叠放在一起,∠BOC=∠AOD,则∠BOD= 70 °.
解:∵∠AOB=∠COD=90°,
∴∠AOB+∠COD
=∠AOB+∠DOB+∠BOC
=∠AOB+∠COD
=90°+90°
=180°,
∵∠BOC=∠AOD,
∴∠AOD+∠AOD=180°,
∴∠AOD=160°,
∴∠BOD=∠AOD﹣∠AOB=160°﹣90°=70°,
故答案为:70.
三.解答题(共8小题,满分60分)
21.(6分)(2022秋•南通期末)如图,∠AOC与∠BOC互为补角,∠BOC与∠BOD互为余角,且∠BOC=4∠BOD.
(1)求∠BOC的度数;
(2)若OE平分∠AOC,求∠BOE的度数.
解:(1)∵∠BOC与∠BOD互为余角,
∴∠BOC+∠BOD=90°.
∵∠BOC=4∠BOD,
∴∠BOC=×90°=72°.
(2)∵∠AOC与∠BOC互为补角,
∴∠AOC+∠BOC=180°.
∴∠AOC=180°﹣∠BOC=180°﹣72°=108°.
∵OE平分∠AOC,
∴∠COE=AOC=108°=54°,
∴∠BOE=∠COE+∠BOC=54°+72°=126°.
22.(6分)(2023春•临清市期中)如图,直线AB,CD相交于点O,OE是∠COB的平分线,FO⊥OE,已知∠AOD=70°.
(1)求∠BOE的度数;
(2)OF平分∠AOC吗?为什么?
解:(1)根据对顶角相等得,∠BOC=∠AOD=70°,
∵OE是∠COB的平分线,
∴∠BOE=∠BOC=35°.
(2)∵∠AOD=70°,∴∠AOC=110°,
而∠FOC=90°﹣∠COE=90°﹣35°=55°,所以OF平分∠AOC.
23.(8分)(2020秋•淮阴区期末)如图,O为直线AB上一点,DO⊥OE,OC平分∠AOD,∠AOC=24°,求∠BOE的度数.
解:∵DO⊥OE,
∴∠DOE=90°,
∵OC平分∠AOD,
∴∠AOC=∠DOC=24°,
∴∠BOE=180°﹣90°﹣24°﹣24°=42°.
24.(8分)(2022秋•建邺区校级期末)如图.
(1)∠AOB的余角为∠AOC,射线OM平分∠AOB,当∠AOB=40°,求∠MOC的度数;
(2)若∠AOB的补角为∠BOD,射线ON平分∠BOD,试用含α的代数式表示∠AON的度数.(画出图形,并直接写出结果)
解:(1)∵∠AOB的余角为∠AOC,∠AOB=40°,
∴∠AOC=90°﹣∠AOB=50°,
∵射线OM平分∠AOB,
∴∠MOA=∠AOC=20°,
∴∠MOC=20°+50°=70°.
(2)如图,∠AOB的补角为∠BOD,∠AOB=α,
∴∠BOD=180°﹣α.
∵射线ON平分∠BOD,
∴∠AON=90°+.
25.(8分)(2022秋•高邮市期末)如图,已知直线AB与CD相交于点O,OE⊥CD于点O、OD是∠BOF的平分线.
(1)若∠BOE=112°,求∠EOF的度数;
(2)∠AOC的补角是 ∠AOD,∠COF,∠BOC ,∠AOC的余角是 ∠AOE,∠EOF .
解:(1)∵∠BOE=112°,OE⊥CD,
∴∠BOD=∠BOE﹣∠DOE=112°﹣90°=22°,
∵OD是∠BOF的平分线,
∴∠BOD=∠DOF=22°,
∴∠EOF=90°﹣∠DOF=68°;
(2)∵∠AOC=∠BOD=∠FOD,
且∠AOC+∠AOD=∠FOD+∠COF=180°,
∴∠AOC的补角是∠AOD和∠COF;
∵∠AOC+∠BOC=180°,
∴∠AOC与∠BOC互补,
综上可知,∠AOC的补角是∠AOD,∠COF,∠BOC;
∵OE⊥CD,
∴∠AOC+∠AOE=∠FOD+∠EOF=90°,
∴∠AOC的余角是∠AOE和∠EOF;
故答案为∠AOD,∠COF,∠BOC;∠AOE,∠EOF.
26.(8分)(2016秋•江阴市期末)如图,直线AB、CD相交于O,∠2﹣∠1=15°,∠3=130°.
(1)求∠2的度数;
(2)试说明OE平分∠COB.
解:(1)∵∠3=130°,∠1+∠3=180°,
∴∠1=180°﹣∠3=50°,
∵∠2﹣∠1=15°,
∴∠2=15°+∠1=65°;
(2)∵∠1=50°,∠2=65°,∠1+∠COE+∠2=180°,
∴∠COE=65°,
∴∠COE=∠2
∴OE平分∠COB.
27.(8分)(2022秋•海门市期末)已知∠AOB=120°,∠COD在∠AOB内部,∠COD=60°.
(1)如图1,若∠BOD=30°,求∠AOC的度数;
(2)如图2,若OE平分∠BOC,请说明:∠AOC=2∠DOE;
(3)如图3,若在∠AOB的外部分别作∠AOC,∠BOD的余角∠AOP,∠BOQ,试探究∠AOP,∠BOQ,∠COD三者之间的数量关系,并说明理由.
解(1)∵∠AOB=120°,∠COD=60°,
∴∠AOC+∠BOD=∠AOB﹣∠COD=120°﹣60°=60°,
∵∠BOD=30°,
∴∠AOC=60°﹣30°=30°;
(2)∵OE平分∠BOC,
∴∠COE=∠BOC,
∵∠EOD=∠COD﹣∠COE,∠COD=60°,
∴∠EOD=60°﹣∠BOC,
∵∠AOC=∠AOB﹣∠BOC,∠AOB=120°,
∴∠AOC=120°﹣∠BOC,
∴∠AOC=2∠EOD;
(3)∵∠AOP+∠AOC=90°,
∴∠AOP=90°﹣∠AOC,
∵∠BOQ+∠BOD=90°,
∴∠BOQ=90°﹣∠BOD,
∴∠AOP+∠BOQ=180°﹣(∠AOC+∠BOD)=180°﹣(∠AOB﹣∠COD),
∵∠AOB=120°,∠COD=60°,
∴∠AOP+∠BOQ=180°﹣(120°﹣60°)=120°=2×60°,
∴∠AOP+∠BOQ=2∠COD.
28.(8分)(2021秋•苏州期末)如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB(其中∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒.
(1)当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间数量关系为 ∠BOC=∠BOE. ;
(2)若射线OC的位置保持不变,且∠COE=130°.
①在旋转的过程中,是否存在某个时刻,使得射线OA,OC,OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意t的值,若不存在,请说明理由;
②如图3,在旋转的过程中,边AB与射线OE相交,请直接写出∠AOC﹣∠BOE的值.
解:(1)∠BOC=∠BOE.
理由如下:
∵∠AOB=90°,
∴∠BOC+∠AOC=90°,∠AOD+∠BOE=90°,
∵OA平分∠COD,
∴∠AOD=∠AOC,
∴∠BOC=∠BOE,
故答案为:∠BOC=∠BOE;
(2)①存在.
理由:∵∠COE=130°,
∴∠COD=180°﹣130°=50°,
当OA平分∠COD时,∠AOD=∠AOC=∠COD,即10t=25,解得t=2.5;
当OC平分∠AOD时,∠AOC=∠COD,即10t﹣50=50,解得t=10;
当OD平分∠AOC时,∠AOD=∠COD,即360﹣10t=50,解得:t=31;
综上所述,t的值为2.5、10、31;
②∵∠AOC=∠COE﹣∠AOE=130°﹣∠AOE,∠BOE=90°﹣∠AOE,
∴∠AOC﹣∠BOE=(130°﹣∠AOE)﹣(90°﹣∠AOE)=40°,
∴∠AOC﹣∠BOE的值为40°
题号
一
二
三
总分
得分
评卷人
得 分
评卷人
得 分
评卷人
得 分
相关试卷
这是一份苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)专题6.2角(专项拔高卷)特训(学生版+解析),共34页。试卷主要包含了2 角,57,5x,,5,,5°,等内容,欢迎下载使用。
这是一份苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)专题6.1线段、射线、直线(专项拔高卷)特训(学生版+解析),共28页。试卷主要包含了1 线段、射线、直线,47,5cmB.6,8cm,那么线段MN的长等于,4 cmB.5,4cm,,5 cm.等内容,欢迎下载使用。
这是一份苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)专题5.1丰富的图形世界(专项拔高卷)特训(学生版+解析),共22页。试卷主要包含了1 丰富的图形世界,61,14),28 ;等内容,欢迎下载使用。








