中考数学考前必刷题型突破方案(安徽专版)专题突破02分析判断函数图象问题(针对第9、10题)(2种类型)特训(原卷版+解析)

这是一份中考数学考前必刷题型突破方案(安徽专版)专题突破02分析判断函数图象问题(针对第9、10题)(2种类型)特训(原卷版+解析)，共56页。
类型1:判断函数图象（2022年9题，2020年10题，2018年10题，2017年9题，2016年9题，2015年10题）
考向1：根据实际问题判断函数图象
考向2：根据函数性质判断函数图象
考向3：根据动态问题判断函数图象
类型2：分析函数图象获取信息（2013年9题）
命题规律与备考策略
类型1:判断函数图象（2022年9题，2020年10题，2018年10题，2017年9题，2016年9题，2015年10题）
考向1：根据实际问题判断函数图象
解决此类问题，主要看以下几点：一看坐标轴，即横轴、纵轴分别表示哪两个量；二看特殊点，特别是起点、终点、拐点以及交点；三看图象的变化趋势，包括增减性，平行于坐标轴的线段表示的意义，比如：路程——时间图中，平行于X轴的线段表示休息（路程不变），而速度——时间图中，平行于X轴的线段表示匀速运动（速度不变）。
考向2：根据函数性质判断函数图象
第一步：根据已知条件确定系数a、b、c的正负；第二步：根据系数a、b、c的正负确定新函数系数正负；第三步：判断新函数的图象。
考向3：根据动态问题判断函数图象
分析判断几何问题的函数图象题目，一般有两种方法：（1）观察法，当函数有明显的增减性差异时，根据题目描述，只需确定函数值在每段函数图象上随着自变量的变化而变化的情况即可得解；（2）计算法，先根据自变量的取值范围对函数进行分段，再求出每段函数的解析式，最后由每段函数的解析式确定函数图象。
类型2：分析函数图象获取信息（2013年9题）
解决分析函数图象获取信息题一般按以下思路进行：（1）分清图象的横、纵坐标代表的量及函数自变量的取值范围；（2）找出分段函数的转折点、函数增减性发生变化的点以及函数图象与坐标轴的交点，根据这些特殊点的坐标求出几何运动特殊位置上的几何量，从而解决问题。
【安徽最新模拟练】
类型1:判断函数图象（2022年9题，2020年10题，2018年10题，2017年9题，2016年9题，2015年10题）
考向1：根据实际问题判断函数图象
1．（2023·安徽合肥·一模）阿基米德说：“给我一个支点，我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理，即“阻力阻力臂动力动力臂”．若已知某一杠杆的阻力和阻力臂分别为和，则这一杠杆的动力和动力臂之间的函数图象大致是（ ）
A．B．
C．D．
2．（2023·安徽·校联考一模）把一个长方体铁块放在如图所示的注满水的圆柱形容器内，容器底部有个水龙头，现打开水龙头按一定的速度放水，1min后将容器内水放完．那么容器内水面的高度与注水时间之间的函数关系图象大致是（ ）
A．B．
C．D．
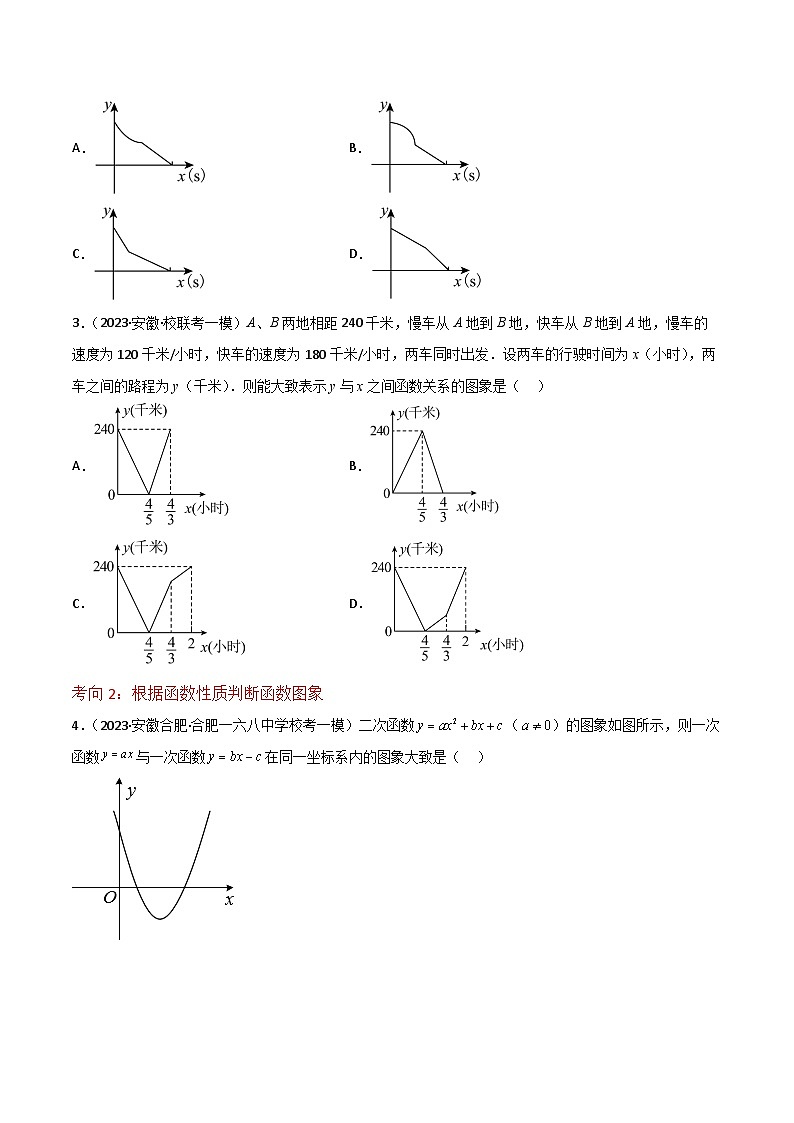
3．（2023·安徽·校联考一模）A、B两地相距240千米，慢车从A地到B地，快车从B地到A地，慢车的速度为120千米/小时，快车的速度为180千米/小时，两车同时出发．设两车的行驶时间为x（小时），两车之间的路程为y（千米）．则能大致表示y与x之间函数关系的图象是（ ）
A．B．
C．D．
考向2：根据函数性质判断函数图象
4．（2023·安徽合肥·合肥一六八中学校考一模）二次函数（）的图象如图所示，则一次函数与一次函数在同一坐标系内的图象大致是（ ）
A．B．
C．D．
5．（2023·安徽蚌埠·校联考一模）关于x的二次函数与反比例函数在同一平面直角坐标系内的大致图象可能是（ ）
A．B．
C．D．
6．（2023·安徽·统考一模）反比例函数与一次函数在同一平面直角坐标系中的图像可能为（ ）
A．B．
C．D．
7．（2023·安徽滁州·校考一模）如图，二次函数的图象经过点A，B，C．现有四个推断：
①抛物线开口向下；
②当时，y取最大值；
③当时．关于x的一元二次方程必有两个不相等的实数根；
④直线经过点A，C，当时，x的取值范围是；
其中推断正确的是（ ）
A．①②B．①③C．①③④D．②③④
考向3：根据动态问题判断函数图象
8．（2023·安徽蚌埠·统考二模）如图，、是的两条互相垂直的直径，点从点出发，沿的路线匀速运动．设（单位为度），那么关于点运动的时间（单位：秒）的函数图象大致是（ ）
A．B．C．D．
9．（2023·安徽·校联考一模）如图，中，，，，点D是边上一动点（不与点A，B重合），过点D作交于点E，点P在边上，连接，若，的面积为y，则下列最能反映y与x之间函数关系的图象是（ ）
A．B．
C．D．
10．（2023·安徽淮北·淮北市第二中学校考二模）如图①，在Rt△ABC中，∠ACB=90°，∠A=30°，动点D从点A出发，沿A→C→B以1cm/s的速度匀速运动到点B，过点D作DE⊥AB于点E，图②是点D运动时，△ADE的面积y（cm2）随时间x（s）变化的关系图像，则AB的长为（ ）
A．4cmB．6cmC．8cmD．10cm
11．（2023·安徽合肥·合肥寿春中学校考模拟预测）如图，点P，Q从边长为2的等边三角形的点B出发，分别沿着，两边以相同的速度在的边上运动，当两点在边上运动到重合时停止．在此过程中，设点P，Q移动过程中各自的路程为x，所得的面积为y，则y随x变化的函数图象大致为（ ）
A．B．
C．D．
12．（2023·安徽黄山·校考模拟预测）如图1，四边形中，，°，，动点从点出发，沿折线方向以m单位/秒的速度匀速运动，在整个运动过程中， 的面积与运动时间（秒）的函数图象如图2所示，则四边形的面积是（ ）
A．144B．134C．124D．114
13．（2023·安徽合肥·校考一模）如图，四边形是边长为的正方形，四边形是边长为的正方形，点与点重合，点，（），在同一条直线上，将正方形沿方向平移至点与点重合时停止，设点、之间的距离为，正方形与正方形重叠部分的面积为，则能大致反映与之间函数关系的图象是（ ）
A．B．
C．D．
14．（2023·安徽淮北·校联考一模）如图，菱形的边长为，，点，在菱形的边上，从点同时出发，分别沿和的方向以每秒的速度运动，到达点时停止，线段扫过区域的面积记为，运动时间记为，能大致反映y与x之间函数关系的图象是（ ）
A．B．
C．D．
15．（2023·安徽池州·校联考一模）如图，正方形的边长为4，点P从点D出发，沿D→C→B→A路线运动．设点P经过的路程为x，的面积为y，则能大致反映y与x的函数关系的图象是（ ）
A．B．C．D．
16．（2023·安徽滁州·校考一模）如图，已知为半圆的直径，，点为半圆上一点（不与点A，重合），于点，，，垂足分别为点，，若，，则与的部分图象大致是（ ）
A．B．
C．D．
17．（2023·安徽合肥·校考一模）如图，斜边均为6的三角板和按如图所示的方式放置，，、在直线上，点C、E重合，固定三角板，将三角板沿直线l向右平移，当点B与点F重合时停止运动，在此过程中，设点B移动的距离为x，两个三角形重叠部分的面积为y，则y关于x的函数图像大致为（ ）
A．B．
C．D．
18．（2023·安徽滁州·统考一模）如图，在四边形中，，，，点是上的一个动点，交四边形另一边于点．设，的面积为，则与之间的函数关系图像可能是（ ）
A．B．C．D．
19．（2023·安徽滁州·校考一模）如图，在中，，，，点，同时从点出发，分别沿、运动，速度都是，直到两点都到达点即停止运动．设点，运动的时间为，的面积为，则与的函数图象大致是（ ）
A．B．
C．D．
20．（2023·安徽亳州·统考模拟预测）如图，在中，，，为边上一动点，交于点，连接，设，，则能表示与之间的函数关系的图象大致是（ ）
A．B．
C．D．
21．（2023·安徽合肥·合肥寿春中学校考一模）如图，半圆O的直径长为4，C是弧的中点，连接、、，点P从A出发沿运动至C停止，过点P作于E，于F．设点P运动的路程为x，则四边形的面积y随x变化的函数图像大致为（ ）
A．B．
C．D．
类型2：分析函数图象获取信息（2013年9题）
22．（2023·安徽·校联考一模）数学是一门可融入日常生活的学科，在研究其他领域中，可以用已知的数学知识对自己的猜想进行验证．某生物研究小组在研究“温度对生菜成熟叶片光合速率和呼吸速率的影响”实验中，得到了一份实验数据，如图所示．不测量长度，结合所学的几何方面的知识，可判断出曲线图中当光合作用相对速率与呼吸作用相对速率差值最大时，处理温度是( )
A．B．C．D．
23．（2023·安徽合肥·模拟预测）骑自行车是一种健康自然的运动旅游方式，长期坚持骑自行车可增强心血管功能，提高人体新陈代谢和免疫力．下图是骑行爱好者老刘2023年2月12日骑自行车行驶路程（km）与时间（h）的关系图象，观察图象得到下列信息，其中错误的是（ ）
A．点表示出发4h，老刘共骑行80km
B．老刘的骑行在0～2h的速度比3~4h的速度慢
C．0~2h老刘的骑行速度为15km/h
D．老刘实际骑行时间为4h
24．（2023·安徽滁州·校考一模）某容器有一个进水管和一个出水管，从某时刻开始的前4分钟内只进水不出水，在随后的8分钟内既进水又出水，12分钟后关闭进水管，放空容器中的水．已知进水管进水的速度与出水管出水的速度是两个常数，容器内水量y（升）与时间x（分钟）之间的关系如图所示．则每分钟的出水量为（ ）
A．4升B．升C．升D．升
25．（2023·安徽合肥·模拟预测）小明、小红两人进行百米赛跑，小明比小红跑的快，如果两人同时跑，小明肯定赢，现在小明让小红先跑若干米，图中的射线a、b分别表示两人跑的路程与小明追赶时间的关系，则小明的速度比小红的速度快（ ）
A．5米/秒B．3.5米/秒C．2.5米/秒D．8米/秒
26．（2023·安徽亳州·统考模拟预测）一个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现，如图所示的是该台灯的电流I（A）与电阻R（）成反比例函数的图象，该图象经过点．根据图象可知，下列说法正确的是（ ）
A．I与R的函数关系式是B．当时，
C．当时，D．当电阻R（）越大时，该台灯的电流I（A）也越大
27．（2023·安徽合肥·合肥市第四十五中学校考一模）甲、乙两位同学放学后走路回家，他们走过的路程（千米）与所用的时间（分）之间的函数关系如图所示．根据图中信息，下列说法正确的是（ ）
A．前10分钟，甲比乙的速度快
B．甲的平均速度为千米/分钟
C．经过30分钟，甲比乙走过的路程少
D．经过20分钟，甲、乙都走了千米
28．（2023·安徽亳州·校考模拟预测）小明积极响应《体质管理通知》中的规定：每天坚持校外1小时体育活动时间，已知小明家、体育场、文具店在同一直线上，下图所反映的过程是：小明从体育场，锻炼了一阵后，走到文具店买笔，然后步行回家．图中表示时间，表示小明离家的距离，则小明从文具店步行回家的速度是（ ）
A．B．C．D．
29．（2023·安徽黄山·统考一模）将盛有凉牛奶的瓶子放在热水中(如图甲所示)，通过热传递方式改变牛奶的内能，图乙是凉牛奶与热水的温度随时间变化的图像．假设热水放出热量全部被牛奶吸收，下列回答错误的是（ ）
A．08min时，热水的温度随时间的增加逐渐降低；
B．08min时，凉牛奶的温度随时间的增加逐渐上升；
C．8min时，热水和凉牛奶的温度相同；
D．0min时，两者的温度差为80．
30．（2023·安徽蚌埠·统考一模）在一条笔直的公路上A、B两地相120km，甲车从A地开往B地，乙车从B地开往A地，甲比乙先出发．设甲、乙两车距A地的路程为y千米，甲车行驶的时间为x小时，y与x之间的关系如图所示，下列说法错误的是（ ）
A．甲车的速度比乙的速度慢B．甲车出发1小时后乙才出发
C．甲车行驶了2.8h或3.2h时，甲、乙两车相距10kmD．乙车达到A地时，甲车离A地90km
【安徽实战真题练】
一、单选题
1．（2022·安徽·统考中考真题）甲、乙、丙、丁四个人步行的路程和所用的时间如图所示，按平均速度计算．走得最快的是（ ）
A．甲B．乙C．丙D．丁
2．（2020·安徽·统考中考真题）如图和都是边长为的等边三角形，它们的边在同一条直线上，点，重合，现将沿着直线向右移动，直至点与重合时停止移动．在此过程中，设点移动的距离为，两个三角形重叠部分的面积为，则随变化的函数图像大致为（ ）
A． B．
C． D．
3．（2015·安徽·统考中考真题）如图，一次函数y1＝x与二次函数y2＝ax2＋bx＋c图象相交于P、Q两点，则函数y＝ax2＋（b－1）x＋c的图象可能是（ ）
A．B．C．D．
4．（2014·安徽·统考中考真题）如图，矩形ABCD中，AB=3，BC=4，动点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数图象大致是（ ）
A．B．
C．D．
5．（2018·安徽·统考中考真题）如图，直线都与直线l垂直，垂足分别为M，N，MN=1，正方形ABCD的边长为，对角线AC在直线l上，且点C位于点M处，将正方形ABCD沿l向右平移，直到点A与点N重合为止，记点C平移的距离为x，正方形ABCD的边位于之间部分的长度和为y，则y关于x的函数图象大致为（ ）
A．B．C．D．
6．（2013·安徽·中考真题）图1所示矩形ABCD中，BC=x，CD=y，y与x满足的反比例函数关系如图2所示，等腰直角三角形AEF的斜边EF过C点，M为EF的中点，则下列结论正确的是
A．当x=3时，EC＜EMB．当y=9时，EC＞EM
C．当x增大时，EC·CF的值增大．D．当y增大时，BE·DF的值不变．
专题突破02分析判断函数图象问题（针对第9、10题）（2种类型）
【安徽十年真题考点及分值细目表】
类型1:判断函数图象（2022年9题，2020年10题，2018年10题，2017年9题，2016年9题，2015年10题）
考向1：根据实际问题判断函数图象
考向2：根据函数性质判断函数图象
考向3：根据动态问题判断函数图象
类型2：分析函数图象获取信息（2013年9题）
命题规律与备考策略
类型1:判断函数图象（2022年9题，2020年10题，2018年10题，2017年9题，2016年9题，2015年10题）
考向1：根据实际问题判断函数图象
解决此类问题，主要看以下几点：一看坐标轴，即横轴、纵轴分别表示哪两个量；二看特殊点，特别是起点、终点、拐点以及交点；三看图象的变化趋势，包括增减性，平行于坐标轴的线段表示的意义，比如：路程——时间图中，平行于X轴的线段表示休息（路程不变），而速度——时间图中，平行于X轴的线段表示匀速运动（速度不变）。
考向2：根据函数性质判断函数图象
第一步：根据已知条件确定系数a、b、c的正负；第二步：根据系数a、b、c的正负确定新函数系数正负；第三步：判断新函数的图象。
考向3：根据动态问题判断函数图象
分析判断几何问题的函数图象题目，一般有两种方法：（1）观察法，当函数有明显的增减性差异时，根据题目描述，只需确定函数值在每段函数图象上随着自变量的变化而变化的情况即可得解；（2）计算法，先根据自变量的取值范围对函数进行分段，再求出每段函数的解析式，最后由每段函数的解析式确定函数图象。
类型2：分析函数图象获取信息（2013年9题）
解决分析函数图象获取信息题一般按以下思路进行：（1）分清图象的横、纵坐标代表的量及函数自变量的取值范围；（2）找出分段函数的转折点、函数增减性发生变化的点以及函数图象与坐标轴的交点，根据这些特殊点的坐标求出几何运动特殊位置上的几何量，从而解决问题。
【安徽最新模拟练】
类型1:判断函数图象（2022年9题，2020年10题，2018年10题，2017年9题，2016年9题，2015年10题）
考向1：根据实际问题判断函数图象
1．（2023·安徽合肥·一模）阿基米德说：“给我一个支点，我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理，即“阻力阻力臂动力动力臂”．若已知某一杠杆的阻力和阻力臂分别为和，则这一杠杆的动力和动力臂之间的函数图象大致是（ ）
A．B．
C．D．
【答案】B
【分析】直接利用阻力阻力臂动力动力臂，进而得出动力关于动力臂的函数关系式，从而确定其图象即可．
【详解】解：∵阻力阻力臂动力动力臂，且阻力和阻力臂分别为和，
∴动力关于动力臂的函数解析式为：，
即，是反比例函数，
又∵动力臂，
故B选项符合题意．
故选：B．
【点睛】本题考查了反比例函数的应用，正确读懂题意得出关系式是解本题的关键．
2．（2023·安徽·校联考一模）把一个长方体铁块放在如图所示的注满水的圆柱形容器内，容器底部有个水龙头，现打开水龙头按一定的速度放水，1min后将容器内水放完．那么容器内水面的高度与注水时间之间的函数关系图象大致是（ ）
A．B．
C．D．
【答案】D
【分析】根据题意可知，在放水的过程中，水面均是匀速下降，下面部分的底面积小于上面部分，所以水面下降速度较快，由此可得出答案．
【详解】解：根据题意可知，按一定的速度放水，所以函数图像均为匀速下降，
由此可排除A，B选项，
当一直放水到刚露出长方体铁块时，底面积是圆柱体的底面积，
所以水面以较慢速度均匀下降，
当开始露出长方体铁后，底面积为圆柱体容器的底面积减去长方体的底面积，
所以水面以较快速度均匀下降，
所以排除C选项，选项D符合题意，
故选：D．
【点睛】本题考查函数图象的意义，深刻理解实际问题中函数图象所代表的意义，是快速解出这道题的关键．
3．（2023·安徽·校联考一模）A、B两地相距240千米，慢车从A地到B地，快车从B地到A地，慢车的速度为120千米/小时，快车的速度为180千米/小时，两车同时出发．设两车的行驶时间为x（小时），两车之间的路程为y（千米）．则能大致表示y与x之间函数关系的图象是（ ）
A．B．
C．D．
【答案】C
【分析】分别求出慢车到达B地、快车到达A地、两车相遇时间，然后分、、三段求出函数关系式，再结合函数图象即可求解．
【详解】解：根据题意得：慢车从A地到B地所用时间为（小时），
快车从B地到A地所用时间为（小时），
两车同时出发，相遇时慢车所用时间为（小时）．
当时，﹔
当时，﹔
当时，；
当时，；
当时，快车已到A地，．
故选：C
【点睛】本题考查了一次函数的应用，理解题意，确定分段函数的解析式，并根据函数解析式确定函数图象是解题关键．
考向2：根据函数性质判断函数图象
4．（2023·安徽合肥·合肥一六八中学校考一模）二次函数（）的图象如图所示，则一次函数与一次函数在同一坐标系内的图象大致是（ ）
A．B．
C．D．
【答案】A
【分析】根据二次函数（）的图象可得，从而得到，，进而得到一次函数经过第一、三象限，一次函数经过第二、三、四象限，即可求解．
【详解】解：根据二次函数（）的图象得：
，
∴，，
∴一次函数经过第一、三象限，一次函数经过第二、三、四象限．
故选：A
【点睛】本题考查二次函数的图象、一次函数的图象、正比例函数的图象和性质，解答本题的关键是明确题意，利用数形结合的思想解答．
5．（2023·安徽蚌埠·校联考一模）关于x的二次函数与反比例函数在同一平面直角坐标系内的大致图象可能是（ ）
A．B．
C．D．
【答案】A
【分析】根据二次函数和反比例函数的图象分和两种情况分析即可．
【详解】解：当时，二次函数的图象开口向下，与y轴的负半轴相交，此时反比例函数的图象在一三象限，故A符合题意，D不符合题意；
当时，二次函数的图象开口向上，与y轴的负半轴相交，此时反比例函数的图象在二四象限，故B，C不符合题意；
故选A．
【点睛】本题考查了二次函数和反比例函数的图象的性质，分类讨论是解答本题的关键．
6．（2023·安徽·统考一模）反比例函数与一次函数在同一平面直角坐标系中的图像可能为（ ）
A．B．
C．D．
【答案】A
【分析】由图象结合性质判断反比例函数中的和一次函数中的的值是否一致即可判断．
【详解】解：A、反比例函数图象在第二、四象限，则，一次函数图象经过二、三、四象限，则，的取值相同，故此选项符合题意；
B、反比例函数图象在第一、三象限，则，一次函数图象经过二、三、四象限，则，的取值不同，故此选项不合题意；
C、反比例函数图象在第一、三象限，则，一次函数图象与轴应交于负半轴，故此选项不合题意；
D、反比例函数图象在第二、四象限，则，一次函数图象经过一、三、四象限，则，，的取值不同，故此选项不合题意；
故选：A．
【点睛】本题主要考查了反比例函数与一次函数的图象，熟练掌握一次函数图象与反比例函数图像是解题的关键．
7．（2023·安徽滁州·校考一模）如图，二次函数的图象经过点A，B，C．现有四个推断：
①抛物线开口向下；
②当时，y取最大值；
③当时．关于x的一元二次方程必有两个不相等的实数根；
④直线经过点A，C，当时，x的取值范围是；
其中推断正确的是（ ）
A．①②B．①③C．①③④D．②③④
【答案】B
【分析】用待定系数法求出二次函数的解析式，再根据二次函数的图象和性质，逐项进行判断即可．
【详解】解：由图象可知点，代入得到，，
解得，
∴二次函数的解析式为，
∵，
∴抛物线开口向下，故①正确；
∵，
∴当时，y取最大值，故②错误；
∵的顶点坐标是，
当时，直线与抛物线有两个交点，
∴关于x的一元二次方程必有两个不相等的实数根；故③正确；
∵直线经过点A，C，
∴当时，x的取值范围是,故④错误，
综上可知，正确是①③，
故选：B
【点睛】此题考查了二次函数的图象和性质，待定系数法求函数解析式，利用图象法判断方程的根和求不等式的解集等知识，熟练掌握二次函数的图象和性质是解题的关键．
考向3：根据动态问题判断函数图象
8．（2023·安徽蚌埠·统考二模）如图，、是的两条互相垂直的直径，点从点出发，沿的路线匀速运动．设（单位为度），那么关于点运动的时间（单位：秒）的函数图象大致是（ ）
A．B．C．D．
【答案】B
【分析】根据图示，分三种情况：（1）当点沿运动时；（2）当点沿运动时；（3）当点沿运动时；分别判断出的取值情况，进而判断出与点运动的时间（单位：秒）的关系图是哪个即可．
【详解】解：当点沿运动时，
当点在点的位置时，，
当点在点的位置时，
，
∴，
由逐渐减小到；
当点沿运动时，
根据圆周角定理，可得；
当点沿运动时，
当点在点的位置时，，
当点在点的位置时，，
由逐渐增加到．
故选：B．
【点睛】本题主要考查了动点的函数图象，圆周角定理，利用分类讨论的思想求解是解题的关键．
9．（2023·安徽·校联考一模）如图，中，，，，点D是边上一动点（不与点A，B重合），过点D作交于点E，点P在边上，连接，若，的面积为y，则下列最能反映y与x之间函数关系的图象是（ ）
A．B．
C．D．
【答案】C
【分析】过点D作于M，过点B作于N，交于F，得到四边形是矩形，即，证明，列得，求出，即可得出函数关系式，由此判断图象．
【详解】过点D作于M，过点B作于N，交于F，
∵，
∴，
∴四边形是矩形，
∴，
∵，
∴，，
∵，
∴，
∴
∴，
∴，
∴，
∵，
∴抛物线开口向下，又，
∴函数图象是以直线为对称轴的抛物线，位于x轴上方的部分，
故选C．
【点睛】此题考查了相似三角形的判定和性质，矩形的判定和性质，求函数关系式，判断函数图象，正确掌握相似三角形的判定求出是解题的关键．
10．（2023·安徽淮北·淮北市第二中学校考二模）如图①，在Rt△ABC中，∠ACB=90°，∠A=30°，动点D从点A出发，沿A→C→B以1cm/s的速度匀速运动到点B，过点D作DE⊥AB于点E，图②是点D运动时，△ADE的面积y（cm2）随时间x（s）变化的关系图像，则AB的长为（ ）
A．4cmB．6cmC．8cmD．10cm
【答案】C
【分析】根据题意，面积最大是，此时D、C两点重合，根据面积公式可求得，再解直角三角形即可得解．
【详解】解：根据题意，面积最大是，此时D、C两点重合，如图所示，
在中，,
∴AD=2DE，AE=，
又，
解得，DE＞0，
∴DE cm，
，
在中，，
∴，
解得cm，
在中，，
cm．
故选择C．
【点睛】本题考查了动点问题和函数图像、勾股定理，30°直角三角形性质；解决问题的关键在于能数形结合看问题、熟练直角三角形性质，勾股定理．
11．（2023·安徽合肥·合肥寿春中学校考模拟预测）如图，点P，Q从边长为2的等边三角形的点B出发，分别沿着，两边以相同的速度在的边上运动，当两点在边上运动到重合时停止．在此过程中，设点P，Q移动过程中各自的路程为x，所得的面积为y，则y随x变化的函数图象大致为（ ）
A．B．
C．D．
【答案】A
【分析】分0≤x≤2和2＜x≤3两部分讨论，当0≤x≤2时，得到，由于当2＜x≤3时，四个选项图象相同，根据二次函数图象与性质即可求解．
【详解】解：如图，当0≤x≤2时，作QD⊥BP，垂足为D，
由题意得△BPQ是等边三角形，
∴BD=BP=x，
∴QD，
∴，
∴当0≤x≤2时，y是x的二次函数，且开口向上，对称轴为y轴，
由于当2＜x≤3时，图象相同，
∴A选项符合条件．
故选：A
【点睛】本题考查了等边三角形的性质，勾股定理，二次函数的图象与性质等知识，理解题意，分类讨论，得到y与x的函数关系式进而确定图象是解题关键．
12．（2023·安徽黄山·校考模拟预测）如图1，四边形中，，°，，动点从点出发，沿折线方向以m单位/秒的速度匀速运动，在整个运动过程中， 的面积与运动时间（秒）的函数图象如图2所示，则四边形的面积是（ ）
A．144B．134C．124D．114
【答案】A
【分析】从图2看，，，过点作交于点，在Rt中，，则，当点在点处时，，解得，则四边形的面积，即可求解．
【详解】解：从图2来看，，
过点作交于点，
则
在中，，
当点在点处时，
解得
则四边形的面积
故选：A
【点睛】本题考查的是动点图象问题，涉及到等腰三角形性质和勾股定理的运用等知识，此类问题关键是：弄清楚不同时间段，图象和图形的对应关系，进而求解．
13．（2023·安徽合肥·校考一模）如图，四边形是边长为的正方形，四边形是边长为的正方形，点与点重合，点，（），在同一条直线上，将正方形沿方向平移至点与点重合时停止，设点、之间的距离为，正方形与正方形重叠部分的面积为，则能大致反映与之间函数关系的图象是（ ）
A．B．
C．D．
【答案】B
【分析】正方形与正方形重叠部分主要分为个部分，属于分段函数；通过列出每一段的函数关系式，得到每一段的函数图象，从而选出正确答案的．
【详解】由，正方形与正方形重叠部分的面积为．则
①；
②；
③
∴
综上可知，图象随着自变量的增大，函数图象如图所示
故选：B．
【点睛】本题主要考查的是动点问题的函数的图象．解题的关键是要根据条件找到所给的两个变量之间的函数关系，尤其是在几何问题中，更要注意基本性质的掌握和灵活运用．
14．（2023·安徽淮北·校联考一模）如图，菱形的边长为，，点，在菱形的边上，从点同时出发，分别沿和的方向以每秒的速度运动，到达点时停止，线段扫过区域的面积记为，运动时间记为，能大致反映y与x之间函数关系的图象是（ ）
A．B．
C．D．
【答案】C
【分析】根据菱形的性质，结合题意，分两种情况讨论，时，当时，根据三角形的面积公式建立函数关系，根据二次函函数的图象的性质即可求解．
【详解】解析：当时，过点作于，如图，
，，
则，
线段扫过区域的面积，图象是开口向上，位于轴右侧的抛物线的一部分，
当时，
如图，过点作于，则，
，
线段扫过区域的面积，
图象是开口向下，位于对称轴直线左侧的抛物线的一部分，
故选：C．
【点睛】本题考查了动点问题的函数图象，菱形的性质，解直角三角形，二次函数图象的性质，掌握二次函数图像的性质是解题的关键．
15．（2023·安徽池州·校联考一模）如图，正方形的边长为4，点P从点D出发，沿D→C→B→A路线运动．设点P经过的路程为x，的面积为y，则能大致反映y与x的函数关系的图象是（ ）
A．B．C．D．
【答案】C
【分析】分点在边、、上三种情况，根据三角形的面积公式分别列式表示出与的关系式，再根据一次函数图象解答．
【详解】解：①点在边上时，点到的距离为，
即，
②点在边上时，点到的距离不变为，
，
③点在边上时，点到的距离为，
，
纵观各选项，只有C选项图象符合．
故选：C．
【点睛】本题考查了动点问题的函数图象，根据点运动的位置的不同，分情况表示出三角形的面积与的关系式是解题的关键，也是本题的难点．
16．（2023·安徽滁州·校考一模）如图，已知为半圆的直径，，点为半圆上一点（不与点A，重合），于点，，，垂足分别为点，，若，，则与的部分图象大致是（ ）
A．B．
C．D．
【答案】A
【分析】利用直径所对的圆周角是直角，可推出四边形是矩形，从而对角线相等，得到值．
【详解】解：连接，，如图所示：
为半圆的直径，
，
，，
四边形为矩形，
，
在中，
，



，
故选：A．
【点睛】本题主要考查了圆周角定理、动点的函数图象，解题的关键是熟练掌握直径所对的圆周角是直角．
17．（2023·安徽合肥·校考一模）如图，斜边均为6的三角板和按如图所示的方式放置，，、在直线上，点C、E重合，固定三角板，将三角板沿直线l向右平移，当点B与点F重合时停止运动，在此过程中，设点B移动的距离为x，两个三角形重叠部分的面积为y，则y关于x的函数图像大致为（ ）
A．B．
C．D．
【答案】A
【分析】分，，三类讨论，结合直角三角形角所对直角边等于斜边一半列出各段解析式即可得到答案；
【详解】解：当，如图（1）所示，由题意可得，
，
∵，
∴的高为：，
∴（），故A、C图像符合题意；
当，如图（2）所示，由题意可得，
∵，
∴，
∴，
∴，，
，故A、C图像符合题意；
当，如图（3）所示，由题意可得，
，
∵，
∴，
∴的高为：，
∴，故只有A选项符合题意；
故选A；
【点睛】本题考查二次函数图像与性质，解直角三角形，等腰三角形性质，解题的关键是分类讨论表示出解析式判断．
18．（2023·安徽滁州·统考一模）如图，在四边形中，，，，点是上的一个动点，交四边形另一边于点．设，的面积为，则与之间的函数关系图像可能是（ ）
A．B．C．D．
【答案】C
【分析】分，，讨论即可．
【详解】解：过点D作于点E，过点C作于点F，则，
∵，
∴，，
又，
∴，
∴，
∴，
当时，
∵，，
∴
∴，
∴，即，
∴，
∴；
当时，此时，
∴，
当时，
同理可证，
∴，即，
∴，
∴，
综上，．
故选：C．
【点睛】本题考查了图形运动与二次函数，相似三角形的判定与性质等，明确题意，找出所求问题需要的条件是解题的关键．
19．（2023·安徽滁州·校考一模）如图，在中，，，，点，同时从点出发，分别沿、运动，速度都是，直到两点都到达点即停止运动．设点，运动的时间为，的面积为，则与的函数图象大致是（ ）
A．B．
C．D．
【答案】D
【分析】根据点，同时从点出发，分别沿、运动，速度都是，可分为三种情况分别讨论：①当点P在AB边，点Q没有到点C处；②当点P在AB边，点Q到达点C处；③当点Q在点C，点P在BC边．
【详解】∵，，，
由勾股定理得，，
∵，
∴，，
∴，△APQ的高，
当点Q到达点C时，即当时，点P在AB边上，
∴分三种情况讨论：
①当点P在AB边，点Q没有到点C处，即时，
；
②当点P在AB边，点Q到达点C处，即时，
∵，
∴△APQ的高，
；
③当点Q在点C，点P在BC边，即时，
∵，，，
∴，，
，
综上根据函数解析式可得图象，
故选D．
【点睛】本题主要考查动点运动，三角形面积以及函数的图象．分情况进行讨论是解答本题的关键．
20．（2023·安徽亳州·统考模拟预测）如图，在中，，，为边上一动点，交于点，连接，设，，则能表示与之间的函数关系的图象大致是（ ）
A．B．
C．D．
【答案】C
【分析】过点作交延长线于点，根据列出解析式再判断即可．
【详解】如图，过点作交延长线于点，
∵
∴
∵，
∴
∴
．
∵
∴
在中，，
，
.
∴当时，，
故选：C.
【点睛】本题考查了二次函数的图象与性质、等腰三角形的判定与性质、勾股定理、平行线的性质，考查了学生从图象中读取信息的数形结合能力，体现了分类讨论的思想．
21．（2023·安徽合肥·合肥寿春中学校考一模）如图，半圆O的直径长为4，C是弧的中点，连接、、，点P从A出发沿运动至C停止，过点P作于E，于F．设点P运动的路程为x，则四边形的面积y随x变化的函数图像大致为（ ）
A．B．
C．D．
【答案】A
【分析】分别根据当点P在上运动和运动两种情况进行讨论，通过C是弧的中点得到是等腰直角三角形，根据，得到四边形为矩形，计算出矩形的边长即可得到面积，从而得到函数表达式，根据二次函数的性质即可得到答案．
【详解】解：∵C是弧的中点，
∴,
∵是直径，
∴是等腰直角三角形，,
∵，
∴，四边形为矩形，
当点P在上运动时，
∵，
∴，，
∴四边形的面积，
当点P在上运动时，，如下图所示，
∵,，，
∴，
∴四边形是矩形，
∵，
∴，
∴四边形的面积，
∴，
∴y随x变化的函数图像大致为A所示，
故选：A
【点睛】本题考查圆和二次函数的性质，解题的关键是根据题意得到函数的表达式．
类型2：分析函数图象获取信息（2013年9题）
22．（2023·安徽·校联考一模）数学是一门可融入日常生活的学科，在研究其他领域中，可以用已知的数学知识对自己的猜想进行验证．某生物研究小组在研究“温度对生菜成熟叶片光合速率和呼吸速率的影响”实验中，得到了一份实验数据，如图所示．不测量长度，结合所学的几何方面的知识，可判断出曲线图中当光合作用相对速率与呼吸作用相对速率差值最大时，处理温度是( )
A．B．C．D．
【答案】B
【分析】观察图形可得答案．
【详解】解：曲线图中当光合作用相对速率与呼吸作用相对速率差值最大时，处理温度是，
故选：B．
【点睛】本题考查了函数图象，解答问题的关键是明确题意，找出所求问题的条件，利用数形结合思想解答．
23．（2023·安徽合肥·模拟预测）骑自行车是一种健康自然的运动旅游方式，长期坚持骑自行车可增强心血管功能，提高人体新陈代谢和免疫力．下图是骑行爱好者老刘2023年2月12日骑自行车行驶路程（km）与时间（h）的关系图象，观察图象得到下列信息，其中错误的是（ ）
A．点表示出发4h，老刘共骑行80km
B．老刘的骑行在0～2h的速度比3~4h的速度慢
C．0~2h老刘的骑行速度为15km/h
D．老刘实际骑行时间为4h
【答案】D
【分析】仔细观察图象，结合路程、速度、时间的关系逐项判断即可．
【详解】解：由图可知，点所对应的路程为80km，时间为4h，即表示出发4h，老刘共骑行80km，故A正确，不符合题意；
0～2h老刘骑行的路程为30km，
0～2h的速度为，
3~4h骑行的路程为，
3~4h的速度为，
，
老刘的骑行在0～2h的速度比3~4h的速度慢，
故B、C正确，不符合题意；
2~3h内的路程没有变化，即老刘处于静止状态，
老刘实际骑行时间为，
故D错误，符合题意；
故选：D．
【点睛】本题考查了函数图象的实际应用，读懂题意，从所给的函数图象中获取信息是解题的关键．
24．（2023·安徽滁州·校考一模）某容器有一个进水管和一个出水管，从某时刻开始的前4分钟内只进水不出水，在随后的8分钟内既进水又出水，12分钟后关闭进水管，放空容器中的水．已知进水管进水的速度与出水管出水的速度是两个常数，容器内水量y（升）与时间x（分钟）之间的关系如图所示．则每分钟的出水量为（ ）
A．4升B．升C．升D．升
【答案】C
【分析】根据图象先求出每分钟进水量，然后根据图象求出既出水又进水时，每分钟进水量，即可求出每分钟出水量．
【详解】解：根据图像可知，4分钟进水量为20L，
∴1分钟进水量为：，
∵8分钟内既进水又出水时，进水量为10L，
∴这段时间内1分钟进水量为：，
∴1分钟出水量为：，故C正确．
故选：C．
【点睛】本题主要考查了从函数图象中获取信息，根据图象得出1分钟进水量和既出水又进水时，1分钟进水量是解题的关键．
25．（2023·安徽合肥·模拟预测）小明、小红两人进行百米赛跑，小明比小红跑的快，如果两人同时跑，小明肯定赢，现在小明让小红先跑若干米，图中的射线a、b分别表示两人跑的路程与小明追赶时间的关系，则小明的速度比小红的速度快（ ）
A．5米/秒B．3.5米/秒C．2.5米/秒D．8米/秒
【答案】C
【分析】小红先跑若干米，说明射线b表示小红的函数图象，由此可求出小红的速度，根据射线a求出小明的速度，进而可求出答案．
【详解】解：由图象可知，小红的速度应为：（64-20）÷8=5.5（米/秒），
小明的速度为：64÷8=8（米/秒），
小明的速度比小红的速度快8-5.5=2.5（米/秒），故C正确．
故选：C．
【点睛】本题考查了函数的图象，难度一般，解题的关键在于熟练掌握图形分析的基本步骤．
26．（2023·安徽亳州·统考模拟预测）一个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现，如图所示的是该台灯的电流I（A）与电阻R（）成反比例函数的图象，该图象经过点．根据图象可知，下列说法正确的是（ ）
A．I与R的函数关系式是B．当时，
C．当时，D．当电阻R（）越大时，该台灯的电流I（A）也越大
【答案】A
【分析】直接利用反比例函数图像得出函数解析式，进而利用反比例函数的性质分析得出答案．
【详解】解：A．设反比例函数解析式为：，把代入得：
，则，故此选项符合题意；
B．当时，，故此选项不合题意；
C．当时，，故此选项不合题意；
D．当电阻越大时，该台灯的电流（A）越小，故此选项不合题意．
故选：A．
【点睛】此题主要考查了反比例函数的应用，正确得出函数解析式是解题关键．
27．（2023·安徽合肥·合肥市第四十五中学校考一模）甲、乙两位同学放学后走路回家，他们走过的路程（千米）与所用的时间（分）之间的函数关系如图所示．根据图中信息，下列说法正确的是（ ）
A．前10分钟，甲比乙的速度快
B．甲的平均速度为千米/分钟
C．经过30分钟，甲比乙走过的路程少
D．经过20分钟，甲、乙都走了千米
【答案】D
【分析】结合函数关系图逐项判断即可．
【详解】解：A项，前10分钟，甲走了千米，乙走了千米，则甲比乙的速度慢，故本选项不符合题意；
B项，甲40分钟走了千米，则其平均速度为：千米/分钟，故本选项不符合题意；
C项，经过30分钟，甲走了千米，乙走了千米，则甲比乙多走了千米，故本选项不符合题意；
D项，前20分钟，根据函数关系图可知，甲、乙都走了千米，，故本选项符合题意；
故选：D．
【点睛】本题考查了一次函数的图象及其在行程问题中的应用，理解函数关系图是解答本题的关键．
28．（2023·安徽亳州·校考模拟预测）小明积极响应《体质管理通知》中的规定：每天坚持校外1小时体育活动时间，已知小明家、体育场、文具店在同一直线上，下图所反映的过程是：小明从体育场，锻炼了一阵后，走到文具店买笔，然后步行回家．图中表示时间，表示小明离家的距离，则小明从文具店步行回家的速度是（ ）
A．B．C．D．
【答案】A
【分析】根据图象信息，即可得出答案．
【详解】根据图象信息得，
文具店离家，从文具店回家用了，
所以文具店步行回家的速度为：，
故答案选A．
【点睛】本题考查了函数图象，正确的理解函数图象横纵坐标表示的意义是解题的关键．
29．（2023·安徽黄山·统考一模）将盛有凉牛奶的瓶子放在热水中(如图甲所示)，通过热传递方式改变牛奶的内能，图乙是凉牛奶与热水的温度随时间变化的图像．假设热水放出热量全部被牛奶吸收，下列回答错误的是（ ）
A．08min时，热水的温度随时间的增加逐渐降低；
B．08min时，凉牛奶的温度随时间的增加逐渐上升；
C．8min时，热水和凉牛奶的温度相同；
D．0min时，两者的温度差为80．
【答案】D
【分析】根据图像可判定A、B、C选项的正误，根据温差的定义可判定D选项．
【详解】解：由图像可知A、B、C选项正确，不符合题意；0min时，两者的温度差为，则D选项错误，符合题意．
故选D．
【点睛】本题主要考查了从图像上获取信息，从图像上正确获取所需信息是解答本题的关键．
30．（2023·安徽蚌埠·统考一模）在一条笔直的公路上A、B两地相120km，甲车从A地开往B地，乙车从B地开往A地，甲比乙先出发．设甲、乙两车距A地的路程为y千米，甲车行驶的时间为x小时，y与x之间的关系如图所示，下列说法错误的是（ ）
A．甲车的速度比乙的速度慢B．甲车出发1小时后乙才出发
C．甲车行驶了2.8h或3.2h时，甲、乙两车相距10kmD．乙车达到A地时，甲车离A地90km
【答案】D
【分析】根据图象直接判断A；求出两车的路程y与时间x之间的函数关系式，即可判断B、C、D
【详解】解：当甲出发时乙未出发，甲行驶5小时未到达B地，而乙已经到达A地，说明甲车的速度比乙的速度慢，故选项A正确；
设甲车的路程y与时间x之间的函数关系式为，代入，
得，
解得，
∴甲车的路程y与时间x之间的函数关系式为；
设乙车的路程y与时间x之间的函数关系式为，代入和，
，解得，
∴乙车的路程y与时间x之间的函数关系式为，
当时，，解得，
即甲车出发1小时后乙才出发，故选项B正确；
当时，解得；
当时，解得；
∴甲车行驶了2.8h或3.2h时，甲、乙两车相距10km，故选项C正确；
当时，，故选项D错误；
故选：D．
【点睛】此题考查了一次函数的图象，求一次函数的解析式，一次函数的应用，正确理解一次函数的图象得到相关信息是解题的关键．
【安徽实战真题练】
一、单选题
1．（2022·安徽·统考中考真题）甲、乙、丙、丁四个人步行的路程和所用的时间如图所示，按平均速度计算．走得最快的是（ ）
A．甲B．乙C．丙D．丁
【答案】A
【分析】根据图象，先比较甲、乙的速度；然后再比较丙、丁的速度，进而在比较甲、丁的速度即可．
【详解】乙在所用时间为30分钟时，甲走的路程大于乙走的路程，故甲的速度较快；
丙在所用时间为50分钟时，丁走的路程大于丙走的路程，故丁的速度较快；
又因为甲、丁在路程相同的情况下，甲用的时间较少，故甲的速度最快，
故选A
【点睛】本题考查了从图象中获取信息的能力，正确的识图是解题的关键．
2．（2020·安徽·统考中考真题）如图和都是边长为的等边三角形，它们的边在同一条直线上，点，重合，现将沿着直线向右移动，直至点与重合时停止移动．在此过程中，设点移动的距离为，两个三角形重叠部分的面积为，则随变化的函数图像大致为（ ）
A． B．
C． D．
【答案】A
【分析】根据图象可得出重叠部分三角形的边长为x,根据特殊角三角函数可得高为,由此得出面积y是x的二次函数,直到重合面积固定,再往右移动重叠部分的边长变为(4－x),同时可得
【详解】C点移动到F点,重叠部分三角形的边长为x,由于是等边三角形,则高为,面积为y=x··=,
B点移动到F点,重叠部分三角形的边长为(4－x),高为,面积为
y=(4－x)··=,
两个三角形重合时面积正好为.
由二次函数图象的性质可判断答案为A,
故选A.
【点睛】本题考查三角形运动面积和二次函数图像性质,关键在于通过三角形面积公式结合二次函数图形得出结论.
3．（2015·安徽·统考中考真题）如图，一次函数y1＝x与二次函数y2＝ax2＋bx＋c图象相交于P、Q两点，则函数y＝ax2＋（b－1）x＋c的图象可能是（ ）
A．B．C．D．
【答案】A
【分析】由一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，得出方程ax2+（b-1）x+c=0有两个不相等的根，进而得出函数y=ax2+（b-1）x+c与x轴有两个交点，根据方程根与系数的关系得出函数y=ax2+（b-1）x+c的对称轴x=-＞0，即可进行判断．
【详解】点P在抛物线上，设点P（x，ax2+bx+c），又因点P在直线y=x上，
∴x=ax2+bx+c，
∴ax2+（b-1）x+c=0；
由图象可知一次函数y=x与二次函数y=ax2+bx+c交于第一象限的P、Q两点，
∴方程ax2+（b-1）x+c=0有两个正实数根．
∴函数y=ax2+（b-1）x+c与x轴有两个交点，
又∵-＞0，a＞0
∴-=-+＞0
∴函数y=ax2+（b-1）x+c的对称轴x=-＞0，
∴A符合条件，
故选A．
4．（2014·安徽·统考中考真题）如图，矩形ABCD中，AB=3，BC=4，动点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数图象大致是（ ）
A．B．
C．D．
【答案】B
【分析】①点P在AB上时，点D到AP的距离为AD的长度，②点P在BC上时，根据同角的余角相等求出∠APB=∠PAD，再利用相似三角形的列出比例式整理得到y与x的关系式，从而得解．
【详解】①点P在AB上时，0≤x≤3，点D到AP的距离为AD的长度，是定值4；
②点P在BC上时，3＜x≤5，
∵∠APB+∠BAP=90°，
∠PAD+∠BAP=90°，
∴∠APB=∠PAD，
又∵∠B=∠DEA=90°，
∴△ABP∽△DEA，
∴= ，
即，
∴y=，
纵观各选项，只有B选项图形符合，
故选B．
5．（2018·安徽·统考中考真题）如图，直线都与直线l垂直，垂足分别为M，N，MN=1，正方形ABCD的边长为，对角线AC在直线l上，且点C位于点M处，将正方形ABCD沿l向右平移，直到点A与点N重合为止，记点C平移的距离为x，正方形ABCD的边位于之间部分的长度和为y，则y关于x的函数图象大致为（ ）
A．B．C．D．
【答案】A
【分析】由已知易得AC=2，∠ACD=45°，分0≤x≤1、1