2023-2024学年河南省周口市郸城县八年级（上）期末数学试卷（含答案）

这是一份2023-2024学年河南省周口市郸城县八年级（上）期末数学试卷（含答案），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列运算正确的是( )
A. x2+x3=x5B. a2⋅a3=a5
C. (2x2)3=8x5D. (x−1)2=x2−1
2.能说明命题“任何数a的平方都大于0.”是假命题的一个反例可以是( )
A. a=−2B. a=0C. a=12D. a=3.14
3.如图，在△ABC中，按以下步骤作图：①分别以点B和C为圆心，以大于12BC的长为半径作弧，两弧相交于点M和N；②作直线MN交AC于点D，连接BD.若AC=6，AD=2，则BD的长为( )
A. 2B. 3C. 4D. 6
4.将图(甲)中阴影部分的小长方形变换到图(乙)位置，根据两个图形的面积关系得到的数学公式是( )
A. (a+b)2=a2+2ab+b2B. (a−b)2=a2−2ab+b2
C. a2−b2=(a+b)(a−b)D. (a+2b)(a−b)=a2+ab−2b2
5.一组数据共40个，分为6组，第1到第4组的频数之和为28，第5组的频率为0.1，则第6组的频数为( )
A. 4B. 6C. 8D. 10
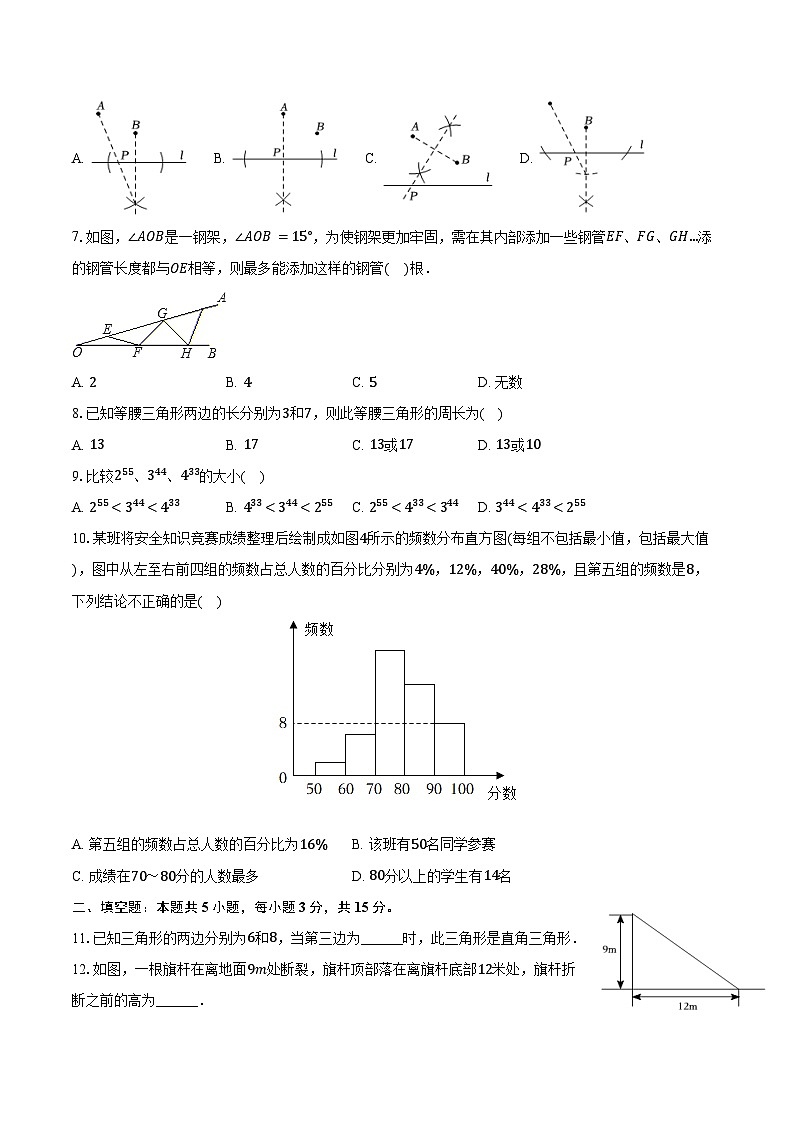
6.已知点A，B是两个居民区的位置，现在准备在墙l边上建立一个垃圾站点P，如图是4位设计师给出的规划图，其中PA+PB距离最短的是( )
A. B. C. D.
7.如图，∠AOB是一钢架，∠AOB=15°，为使钢架更加牢固，需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等，则最多能添加这样的钢管( )根．
A. 2B. 4C. 5D. 无数
8.已知等腰三角形两边的长分别为3和7，则此等腰三角形的周长为( )
A. 13B. 17C. 13或17D. 13或10
9.比较255、344、433的大小( )
A. 255<344<433B. 433<344<255C. 255<433<344D. 344<433<255
10.某班将安全知识竞赛成绩整理后绘制成如图4所示的频数分布直方图(每组不包括最小值，包括最大值)，图中从左至右前四组的频数占总人数的百分比分别为4%，12%，40%，28%，且第五组的频数是8，下列结论不正确的是( )
A. 第五组的频数占总人数的百分比为16%B. 该班有50名同学参赛
C. 成绩在70～80分的人数最多D. 80分以上的学生有14名
二、填空题：本题共5小题，每小题3分，共15分。
11.已知三角形的两边分别为6和8，当第三边为______时，此三角形是直角三角形．
12.如图，一根旗杆在离地面9m处断裂，旗杆顶部落在离旗杆底部12米处，旗杆折
断之前的高为______．
13.如图，在△ABC中，AD平分∠BAC，DE⊥AB.若AC=4，DE=2，则S△ACD= ______．
14.边长为a的正方形ABCD与边长为b的正方形DEFG按如图所示的方式摆放，点A，D，G在同一直线上.已知a+b=10，ab=24.则图中阴影部分的面积为______．
15.在长方形ABCD中，AB=5，BC=12，点E是边AD上的一个动点，把△BAE沿BE折叠，点A落在A′处，当△A′DE是直角三角形时，DE的长为______．
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题8分)
计算：
(1)−12+ 16+| 2−1|+3−8；
(2)简便运算：20222−2023×2021．
17.(本小题8分)
先化简，再求值：(2m+1)(2m−1)−(m−1)2+(2m)3÷(−8m)，其中m2+m−2=0．
18.(本小题8分)
因式分解：
(1)3x3−12xy2；
(2)−a2−4b2+4ab．
19.(本小题10分)
如图，Rt△ABC中，∠C=90°，AC=12，BC=16．
(1)AB的长为______．
(2)把△ABC沿着直线AD翻折，使得点C落在AB边上E处，求CD的长．
20.(本小题10分)
如图，在△ABC中，AB=AC，D是BA延长线上一点，点E是AC的中点．
(1)实践与操作：利用尺规按下列要求作图，并在图中标明相应字母(保留作图痕迹，不写作法)．
①作∠DAC的平分线AM；连接BE，并延长交AM于点G；
②过点A作BC的垂线，垂足为F．
(2)猜想与证明：猜想AG与BF有怎样的位置关系与数量关系，并说明理由．
21.(本小题11分)
教育部在《大中小学劳动教育指导纲要(试行)》中明确要求：中小学劳动教育课平均每周不少于1课时，初中生平均每周劳动时间不少于3小时.某初级中学为了解学生劳动教育的情况，从本校学生中随机抽取了500名进行问卷调查，如图是根据此次调查结果得到的统计图．

请根据统计图回答下列问题：
(1)在扇形统计图中，最喜欢的劳动课程为“木工”的圆心角度数是______°；
(2)求本次调查中，平均每周劳动时间符合教育部要求的人数占被调查人数的百分比？
(3)请你根据本次问卷调查的结果给同学和学校各提一条合理化建议．
22.(本小题8分)
【观察】请你观察下列式子．
第1个等式： 1=1．
第2个等式： 1+3=2．
第3个等式： 1+3+5=3．
第4个等式： 1+3+5+7=4．
第5个等式： 1+3+5+7+9=5．
【发现】根据你的阅读回答下列问题：
(1)写出第7个等式______．
(2)请根据上面式子的规律填空： 1+3+5+⋯+(2n+1)=______．
(3)利用(2)中结论计算： 4+12+20+28+⋯+42+52．
23.(本小题12分)
两个顶角相等的等腰三角形，如果具有公共的顶角顶点，并将它们的底角顶点分别对应连接起来得到两个全等三角形，我们把这样的图形称为“手拉手”图形．如图1，在“手拉手”图形中，AB=AC，AD=AE，∠BAC=∠DAE，连结BD，CE，则△ABD≌△ACE．
(1)请证明图1的结论成立；
(2)如图2，△ABC和△AED是等边三角形，连接BD，EC交于点O，求∠BOC的度数；
(3)如图3，AB=BC，∠ABC=∠BDC=60°，试探究∠A与∠C的数量关系．
参考答案
1.B
2.B
3.C
4.C
5.C
6.A
7.C
8.B
9.C
10.D
11.10或2 7
12.24米
13.4
14.14
15.263或7
16.解：(1)原式=−1+4+ 2−1−2
= 2；
(2)原式=20222−(2022+1)×(2022−1)
=20222−20222+1
=1．
17.解：原式=4m2−1−(m2−2m+1)+8m3÷(−8m)
=4m2−1−m2+2m−1−m2
=2m2+2m−2
=2(m2+m)−2，
因为m2+m−2=0，
所以m2+m=2，
当m2+m=2时，原式=2×2−2=2．
18.解：(1)3x3−12xy2
=3x(x2−4y2)
=3x(x+2y)(x−2y)；
(2)−a2−4b2+4ab
=−(a2−4ab+4b2)
=−(a−2b)2．
19.(1)20．
(2)根据折叠可得：∠C=∠AED=90°，AC=AE=12，CD=ED，则BE=8，
设CD=DE=x，则DB=16x，
∵DE2+EB2=DB2，
∴(16−x)2=82+x2，
解得：x=6．
即CD=6．
20.解：(1)如图；
(2)AG//BF，AG=2BF.理由如下：
∵AB=AC，
∴∠ABC=∠C，
∴∠DAC=∠ABC+∠C=2∠C，
∵AM平分∠ABC，
∴∠DAC=2∠GAC，
∴∠GAC=∠C
∴AG//BC，即AG/​/BF；
∵点E是AC的中点，
∴AE=CE，
在△AEG和△CEB中，
∠GAE=∠CAE=CE∠AEG=∠CEB，
∴△AEG≌△CEB，
∴AG=CB，
∵AB=AC，AF⊥BC，
∴BF=CF，
∴BC=2BF，
∴AG=2BF．
21.(1)57.6；
(2)500−130−180−85500×100%=21%，
∴符合教育部要求的人数占被调查人数的百分比为21%；
(3)答案不唯一，合理即可，如：
建议学生积极参加学校的劳动课程，多做家务等等；建议学校增设特色劳动课程，增加劳动课的课时等．
22.解：(1) 1+3+5+7+9+11+13=7；
(2)n+1；
(3)根据(2)中的规律可知， 4+12+20+28+⋯+42+52= 4(1+3+5+7+9+11+13)= 4×1+132=14．
23.解：(1)证明：∵∠BAC=∠DAE，
∴∠BAC+∠CAD=∠DAE+∠CAD，
∴∠BAD=∠CAE，
在△ABD和△ACE中，
AB=AC∠BAD=∠CAEAD=AE，
∴△ABD≌△ACE(SAS)；
(2)如图2，∵△ABC和△ADE是等边三角形，
∴AB=AC，AD=AE，∠BAC=∠DAE=60°，
∴∠BAD=∠CAE，
在△ABD和△ACE中，
AB=AC∠BAD=∠CAEAD=AE，
∴△ABD≌△ACE(SAS)，
∴∠ADB=∠AEC，
记AD与CE的交点为G，
∵∠AGE=∠DGO，
∴180°−∠ADB−∠DGO=180°−∠AEC−∠AGE，
∴∠DOE=∠DAE=60°，
∴∠BOC=60°；
(3)∴∠A+∠BCD=180°.理由：
如图3，延长DC至P，使DP=DB，
∵∠BDC=60°，
∴△BDP是等边三角形，
∴BD=BP，∠DBP=60°，
∵∠ABC=60°=∠DBP，
∴∠ABD=∠CBP，
∵AB=CB，
在△ABD和△CBP中
BD=BP∠ABD=∠CBPAB=CB
∴△ABD≌△CBP(SAS)，
∴∠BCP=∠A，
∵∠BCD+∠BCP=180°，
∴∠A+∠BCD=180°．