初中数学湘教版（2024）七年级上册（2024）第1章 有理数精品教学ppt课件

这是一份初中数学湘教版（2024）七年级上册（2024）第1章 有理数精品教学ppt课件，文件包含1511有理数的乘法课件pptx、1511有理数的乘法教学设计docx、有理数大单元教学设计docx等3份课件配套教学资源，其中PPT共28页， 欢迎下载使用。

1.掌握有理数的乘法法则，能利用乘法法则正确进行有理数乘法运算.2.经历探索、归纳有理数乘法法则的过程，发展学生观察、归纳、猜测、验证等能力.3.通过学生自己探索出乘法法则，让学生获得成功的喜悦.
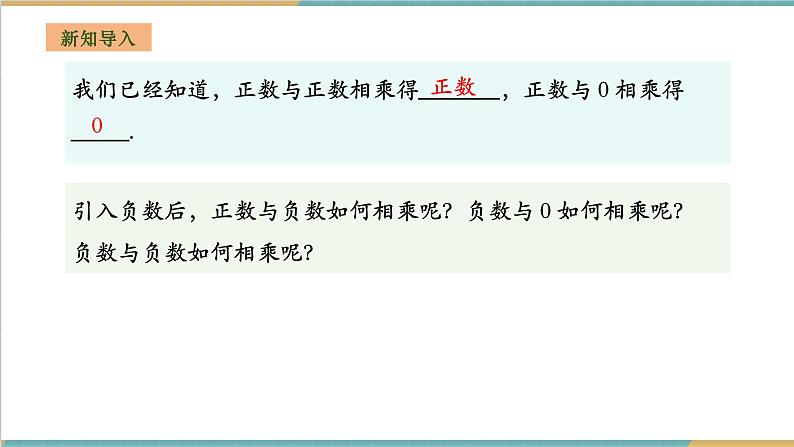
我们已经知道，正数与正数相乘得_______，正数与 0 相乘得 _____.
引入负数后，正数与负数如何相乘呢？负数与 0 如何相乘呢？负数与负数如何相乘呢？
探究（1） 3 ×（-5）应当规定为多少？（2）（-5）×（-3）应当规定为多少？
对于（1），为了满足有理数的乘法对加法的分配律，则有3 ×（-5）+ 3 × 5 = 3 ×[（-5）+ 5 ]= 3 × 0 = 0.
这表明3 ×（-5）与3 × 5互为相反数，于是有3 ×（-5）=-（3 × 5）.
同理可得（-5）× 3 =-（5 × 3），0 ×（-5）= 0，（-5）× 0 = 0
因此，为了满足有理数的乘法对加法的分配律，就必须规定：正数与负数相乘得负数，并把绝对值相乘；0与负数相乘得0.
否则，不可能满足有理数的乘法对加法的分配律.
同样，对于（2），为了满足有理数的乘法对加法的分配律，则有（-5）×（-3）+（-5）× 3 =（-5）×[（-3）+ 3 ]=（-5）× 0 = 0.
这表明（-5）×（-3）与（-5）× 3互为相反数，于是有（-5）×（-3）=-[（-5）× 3 ]=-[-（5 × 3）]= 5 × 3.
因此，为了满足有理数的乘法对加法的分配律，就必须规定：负数与负数相乘得正数，并把绝对值相乘.
【总结归纳】有理数的乘法法则：
同号两数相乘得正数，异号两数相乘得负数，并把绝对值相乘；0乘任何数都得0.
【例1】计算：（1） 3 ×（-2）；（2）（-8）× 5；（3） 0 ×（-6. 18）；
方法指导：两个非零有理数相乘，先确定积的符号，再确定积的绝对值.
【归纳总结】(1)两个有理数相乘，当因数中有带分数时，应先把带分数化为假分数再相乘;当因数中既有分数又有小数时，可根据两个数的特点，先把分数化为小数或把小数化为分数再相乘.(2)一个数乘以1等于它本身，一个数乘以-1等于它的相反数。
【知识技能类作业】必做题：
1.给出下列计算：①(-2)×(-7)=-14; ②( -3) ×15 =-45；③( -7)×0=-7；④1×(-30)=-30. 其中正确的有( ).A.1个 B.2个C.3个 D.4个
2.有理数a，b在数轴上对应点的位置如图所示，则下列各式中正确的是( ).A. a+b<0B. a-b<0C. ab<0D. |b|>a
3.下列说法中，错误的是(　　)A．一个数同1相乘，仍得这个数B．一个数同-1相乘，得原数的相反数C．互为相反数的两数的积为1D．一个数同0相乘，得0
4.计算：(1)(＋4)×(－5)； (2)(－0.125)×(－8)；(3)(－2)×0＋5.
解：（1）(＋4)×(－5)＝－(4×5)＝－20；
（3）(－2)×0＋5＝0＋5＝5.
（2）(－0.125)×(－8)＝0.125×8＝1；
【知识技能类作业】选做题：
5.已知两个有理数a，b，如果ab＜0且a＋b＞0，那么(　　)A．a＞0，b＞0B．a＜0，b＜0C．a，b同号D．a，b异号，且正数的绝对值较大
6.在古代，人们通过在绳子上打结来计数，即“结绳记数”，当时有位父亲为了准确记录孩子的出生天数，在粗细不同的绳子上打结(如图)，由细到粗(右细左粗)，满七进一，那么孩子已经出生了(　　)A．1335天 B．516天C．435天 D．54天
7.一辆出租车在一条东西走向的大街上行驶，这辆出租车连续送客20次，其中8次向东行驶，12次向西行驶，向东每次行驶10 km，向西每次行驶7 km.(1)该出租车连续20次送客后，停在何处？
解：记向东为正，向西为负．8×(＋10)＋12×(－7)＝80－84＝－4(km)．答：停在出发点西边4 km处．
7.一辆出租车在一条东西走向的大街上行驶，这辆出租车连续送客20次，其中8次向东行驶，12次向西行驶，向东每次行驶10 km，向西每次行驶7 km.(2)该出租车一共行驶了多少千米的路程？
解：8×|＋10|＋12×|－7|＝80＋84＝164(km)．答：该出租车一共行驶了164 km的路程．
1.有理数的乘法法则：同号两数相乘得正数，异号两数相乘得负数，并把绝对值相乘；0乘任何数都得0.
2.两个非零有理数相乘，先确定积的符号，再确定积的绝对值.
1.下列算式的运算结果是负数的是(　　).A．0×(－5) B．(－1)×(－2)C．(－3)×3 D．|－2|×|＋4|
2.下列结论不正确的是(　　).A．异号两数相乘，积为负数B．同号两数相乘，积为正数C．两个非负数相乘，积为正数D．两个非正数相乘，积为非负数
3.小明在数轴上标出A，B两点，已知这两点在原点两侧，且到原点的距离相等，则这两点所表示的两数的(　　).A．和为正数 B．和为负数C．积为正数 D．积为负数
4.已知有理数x，y满足x＋y＜0，xy＜0，x＜y，则有(　　)A．x＜0，y＞0，x的绝对值较大B．x＞0，y＜0，y的绝对值较大C．x＞0，y＜0，x的绝对值较大D．x＜0，y＞0，y的绝对值较大
5.已知：|x|＝8，|y|＝5. （1）若x＞y，求xy的值；
解：因为|x|＝8，|y|＝5，所以x＝±8，y＝±5.若x＞y，则x＝8，y＝±5.当x＝8，y＝5时，xy＝8×5＝40；当x＝8，y＝－5时，xy＝8×(－5)＝－40，故xy的值为40或－40.