第28讲 余弦定理、正弦定理应用举例高考数学复习课件

这是一份第28讲 余弦定理、正弦定理应用举例高考数学复习课件，共60页。PPT课件主要包含了教师备用习题，作业手册，ACD等内容，欢迎下载使用。

第四单元 三角函数、解三角形
第28讲 余弦定理、正弦定理应用举例
1.能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
2.能利用正弦定理、余弦定理解决三角形中的最值和范围问题.
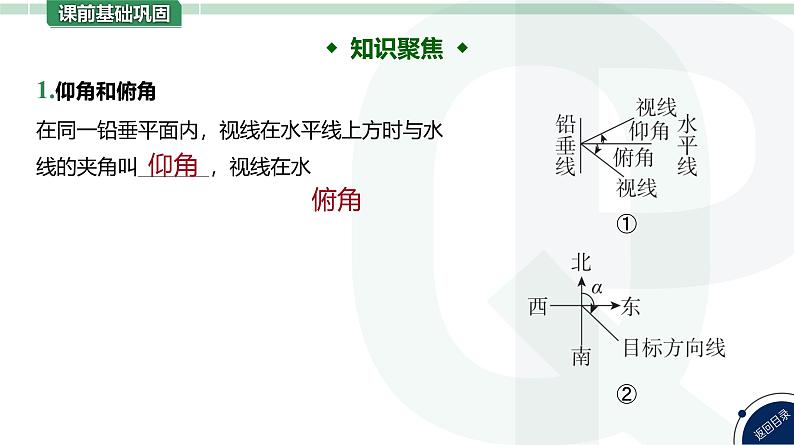
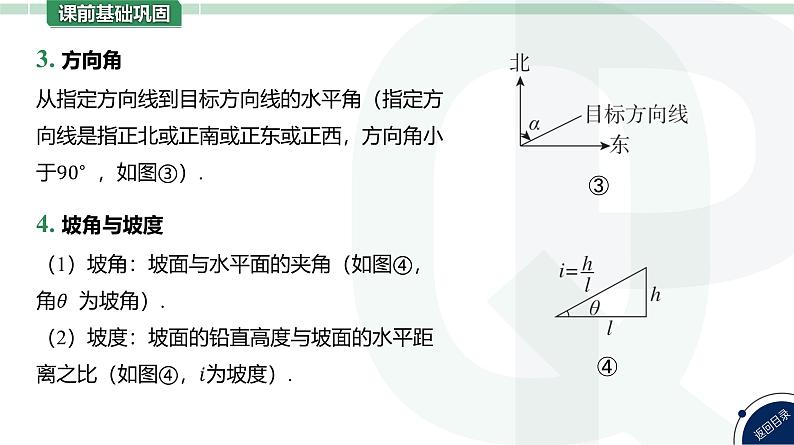
◆ 索引：仰角、俯角的概念不清致误;方向角、方位角的概念不清致误.
探究点一 测量距离问题
[总结反思]测量距离问题的解题步骤:
（1）选定或确定要创建的三角形,首先确定所求量所在的三角形,若其他量已知则直接求解;若有未知量,则把未知量放在另一确定的三角形中求解.（2）确定用正弦定理还是余弦定理求解,如果都可用,那么就选择更便于计算的定理.
A.39米B.43米C.49米D.53米
探究点二 测量高度问题
（1）在测量高度时,要理解仰角、俯角的概念,仰角和俯角都是在同一铅垂面内视线与水平线之间的夹角.
（2）要根据题意正确画出图形,同时空间图形和平面图形要区分开,以免影响解答.
探究点三 测量角度问题
（1）先明确题中所给各个角的含义,然后分析题意,分析已知和所求,再根据题意画出正确的示意图,这是最关键和最主要的一步.（2）将实际问题转化为可用数学方法解决的问题后,再确定使用正弦定理还是余弦定理解决问题.
【备选理由】例1是测量距离的问题，考查了正弦定理的应用;例2是测量高度的问题，以滕王阁为背景，考查余弦定理的实际应用;例3是测量角度的问题;例4作为对前面例题的补充,希望能提高学生的解题能力.
例1 ［配例1使用］ [2023·哈尔滨六中二模] 火箭造桥技术是我国首创在陡峭山区建桥的一种方法.由两枚火箭牵引两条足够长的绳索精准地射入对岸的指定位置，是建造高空悬索桥的关键.位于湖北省的四渡河大桥就是首次用这种
（1） 当走私船发现了巡逻艇时，两者相距多少海里？
（2） 巡逻艇应该沿什么方向去追，才能最快追上走私船？
Unit 2 Explring English
更多高考资料尽在公众号《全元高考》