2024-2025学年陕西省三原县数学九上开学复习检测试题【含答案】

这是一份2024-2025学年陕西省三原县数学九上开学复习检测试题【含答案】，共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）正方形有而矩形不一定有的性质是（ ）
A．四个角都是直角B．对角线相等
C．对角线互相平分D．对角线互相垂直
2、（4分）下列性质中，菱形具有而矩形不一定具有的是（ ）.
A．对角线相等；B．对角线互相平分；
C．对角线互相垂直；D．对角相等
3、（4分）下列事件是随机事件的是 （ ）
A．购买一张福利彩票，中特等奖
B．在一个标准大气压下，纯水加热到100℃，沸腾
C．任意三角形的内角和为180°
D．在一个仅装着白球和黑球的袋中摸出红球
4、（4分）如图，在中，，，将绕点旋转，当点的对应点落在边上时，点的对应点，恰好与点、在同一直线上，则此时的面积为（ ）
A．240B．260C．320D．480
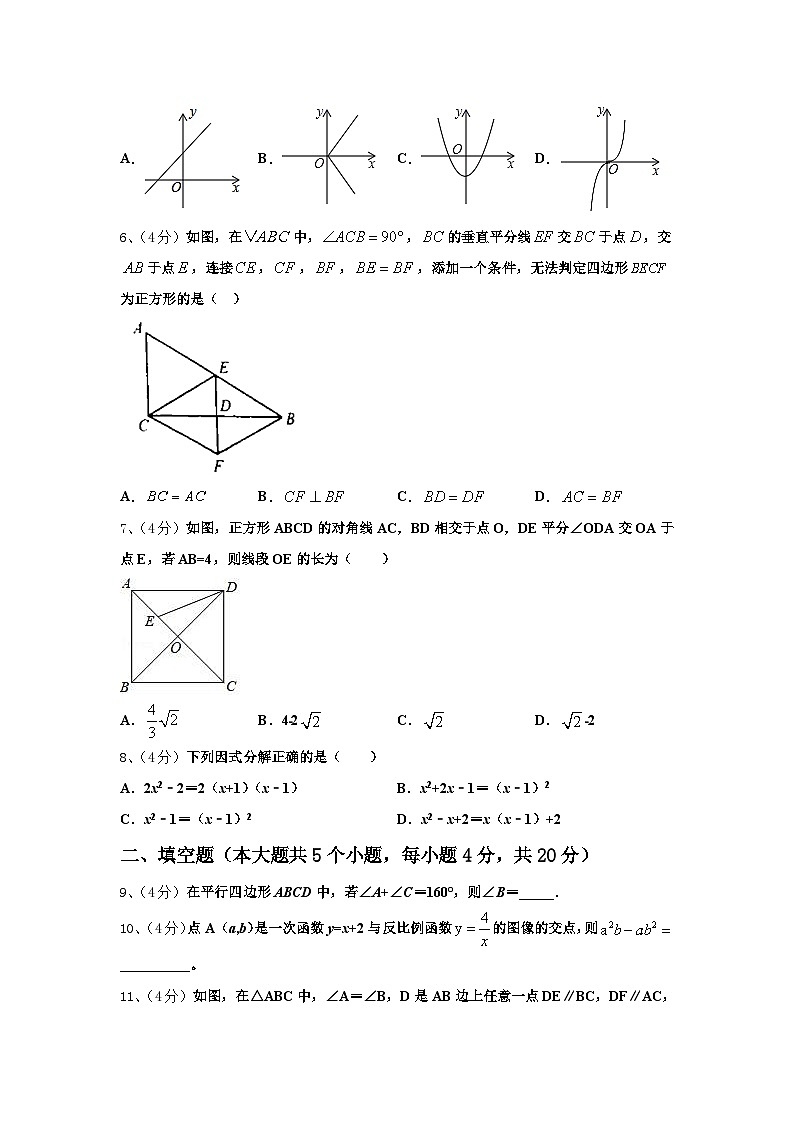
5、（4分）下列各图象中，不是y关于x的函数图象的是（ ）
A．B．C．D．
6、（4分）如图，在中，，的垂直平分线交于点，交于点，连接，，，，添加一个条件，无法判定四边形为正方形的是（ ）
A．B．C．D．
7、（4分）如图，正方形ABCD的对角线AC，BD相交于点O，DE平分∠ODA交OA于点E，若AB=4，则线段OE的长为（ ）
A．B．4﹣2C．D．﹣2
8、（4分）下列因式分解正确的是（ ）
A．2x2﹣2＝2（x+1）（x﹣1）B．x2+2x﹣1＝（x﹣1）2
C．x2﹣1＝（x﹣1）2D．x2﹣x+2＝x（x﹣1）+2
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）在平行四边形ABCD中，若∠A+∠C＝160°，则∠B＝_____．
10、（4分）点A（a,b）是一次函数y=x+2与反比例函数的图像的交点，则__________。
11、（4分）如图，在△ABC中，∠A＝∠B，D是AB边上任意一点DE∥BC，DF∥AC，AC＝5cm，则四边形DECF的周长是_____．
12、（4分）12位参加歌唱比赛的同学的成绩各不相同，按成绩取前6名进入决赛，如果小亮知道了自己的成绩后，要判断能否进入决赛，在平均数、众数、中位数和方差四个统计量中，小亮应该最关注的一个统计量是_____．
13、（4分）如图，在正方形ABCD中，AB＝8，E是BC的中点，点P是对角线AC上一动点，则PE+PB的最小值为_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）化简求值：，其中a=1．
15、（8分）问题提出：
（1）如图1，在中，，点D和点A在直线的同侧，，，，连接，将绕点A逆时针旋转得到，连接（如图2），可求出的度数为______．
问题探究：
（2）如图3，在（1）的条件下，若，，且， ，
①求的度数．
②过点A作直线，交直线于点E，．请求出线段的长．

16、（8分）如图
如图1，四边形ABCD和四边形BCMD都是菱形，
（1）求证：∠M=60°
（2）如图2，点E在边AD上，点F在边CM上，连接EF交CD于点H，若AE=MF，求证：EH=HF；
（3）如图3，在第(2)小题的条件下，连接BH，若EF⊥CM，AB=3，求BH的长
17、（10分）某公司对应聘者A，B进行面试，并按三个方面给应聘者打分，每方面满分20分，打分结果如下表：
根据实际需要，公司将专业知识、工作经验和仪表形象三项成绩得分按6：1：3的比例确定两人的成绩，通过计算说明谁将被录用．
18、（10分）如图1，在△ABC中，AB＝AC，D、E是BC边上的点，连接AD、AE，以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，连接D′C，若BD＝CD′．
（1）求证：△ABD≌△ACD′；
（1）如图1，若∠BAC＝110°，探索BD，DE，CE之间满足怎样的数量关系时，△CD′E是正三角形；
（3）如图3，若∠BAC＝90°，求证：DE1＝BD1+EC1．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）方程在实数范围内的解是_____.
20、（4分）分解因式：a2－4＝________．
21、（4分）如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点，当AB:AD=___________时，四边形MENF是正方形．
22、（4分）如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论：
①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④FH=BD
其中正确结论的为______（请将所有正确的序号都填上）．
23、（4分）已知、、是反比例函数的图象上的三点，且，则、、的大小关系是________________．
二、解答题（本大题共3个小题，共30分）
24、（8分）某校为了开展读书月活动，对学生最喜欢的图书种类进行了一次抽样调查，所有图书分成四类：艺术、文学、科普、其他．随机调查了该校m名学生（每名学生必选且只能选择一类图书），并将调查结果制成如下两幅不完整的统计图：
根据统计图提供的信息，解答下列问题：
（1）m＝ ，n＝ ，并请根据以上信息补全条形统计图；
（2）扇形统计图中，“艺术”所对应的扇形的圆心角度数是 度；
（3）根据抽样调查的结果，请你估计该校900名学生中有多少学生最喜欢科普类图书．
25、（10分）如图，矩形的面积为20cm2，对角线交于点，以AB、AO为邻边作平行四边形，对角线交于点；以为邻边作平行四边形；…；依此类推，则平行四边形的面积为______，平行四边形的面积为______.
26、（12分）已知在▱ABCD中，点E、F在对角线BD上，BE＝DF，点M、N在BA、DC延长线上，AM＝CN，连接ME、NF．试判断线段ME与NF的关系，并说明理由．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
根据正方形与矩形的性质对各选项分析判断后利用排除法求解．
【详解】
解：A、正方形和矩形的四个角都是直角，故本选项错误；
B、正方形和矩形的对角线相等，故本选项错误；
C、正方形和矩形的对角线互相平分，故本选项错误；
D、正方形的对角线互相垂直平分，矩形的对角线互相平分但不一定垂直，故本选项正确．
故选D．
本题考查了正方形和矩形的性质，熟记性质并正确区分是解题的关键．
2、C
【解析】
根据矩形和菱形的性质即可得出答案
【详解】
解：A. 对角线相等是矩形具有的性质，菱形不一定具有；
B. 对角线互相平分是菱形和矩形共有的性质；
C. 对角线互相垂直是菱形具有的性质，矩形不一定具有；
D. 邻边互相垂直是矩形具有的性质，菱形不一定具有．
故选：C．
本题考查矩形和菱形的性质，掌握矩形和菱形性质的区别是解题关键
3、A
【解析】
选项A， 购买一张福利彩票，中特等奖，是随机事件；选项B，在一个标准大气压下，纯水加热到100℃，沸腾，是必然事件；选项C， 任意三角形的内角和为180°，是必然事件；选项D， 在一个仅装着白球和黑球的袋中摸出红球，是不可能事件.故选A.
4、A
【解析】
根据旋转的性质可得，因此可得为等腰三角形，故可得三角形的高，进而计算的面积.
【详解】
根据旋转的性质可得
因此为等腰三角形
，
等腰三角形的高为：

故选A.
本题主要考查图形的旋转和等腰三角形的性质，难点在于根据题意求出高.
5、B
【解析】
根据函数的定义可知，满足对于x的每一个取值，y都有唯一确定的值与之对应关系，据此即可确定函数的个数．
【详解】
解:由函数的定义可知，
每一个给定的x，都有唯一确定的y值与其对应的才是函数，
故选项A、C、D中的函数图象都是y关于x的函数，B中的不是，
故选：B．
主要考查了函数的定义．函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．
6、D
【解析】
根据中垂线的性质：中垂线上的点到线段两个端点的距离相等，有BE=EC，BF=FC进而得出四边形BECF是菱形；由菱形的性质知，以及菱形与正方形的关系，进而分别分析得出即可．
【详解】
解：∵EF垂直平分BC，
∴BE=EC，BF=CF，
∵BF=BE，
∴BE=EC=CF=BF，
∴四边形BECF是菱形；
当BC=AC时，
∵∠ACB=90°，
则∠A=45°时，菱形BECF是正方形．
∵∠A=45°，∠ACB=90°，
∴∠EBC=45°
∴∠EBF=2∠EBC=2×45°=90°
∴菱形BECF是正方形．
故选项A正确，但不符合题意；
当CF⊥BF时，利用正方形的判定得出，菱形BECF是正方形，故选项B正确，但不符合题意；
当BD=DF时，BC=EF，对角线相等的菱形是正方形，得菱形BECF是正方形，故选项C正确，但不符合题意；
当AC=BF时，AC=BF=CE，∠A=∠CEA=∠FBA，由菱形的对角线平分对角和直角三角形的两锐角互余得：∠ABC=30°，即∠FBE=60°，所以无法得出菱形BECF是正方形，故选项D错误，符合题意．
故选D．
本题考查菱形的判定和性质及中垂线的性质、直角三角形的性质、正方形的判定等知识，熟练掌握正方形的判定是解题关键．
7、B
【解析】
如图，过E作EH⊥AD于H，则△AEH是等腰直角三角形，
∵AB=4，△AOB是等腰直角三角形，
∴AO=AB×cs45°=4×=2，
∵DE平分∠ODA，EO⊥DO，EH⊥DH，
∴OE=HE，
设OE=x，则EH=AH=x，AE=2-x，
∵Rt△AEH中，AH2+EH2=AE2，
∴x2+x2=（2-x）2，
解得x=4-2
（负值已舍去），
∴线段OE的长为4-2．
故选：B．
【点睛】考查正方形的性质，解决问题的关键是作辅助线构造直角三角形，运用勾股定理列方程进行计算．
8、A
【解析】
由题意根据因式分解的意义，即可得答案判断选项．
【详解】
解：A、2x2﹣2＝2（x2﹣1）＝2（x+1）（x﹣1），故A符合题意；
B、x2+2x+1＝（x+1）2，故B不符合题意；
C、x2﹣1＝（x+1）（x﹣1），故C不符合题意；
D、不能分解，故D不符合题意；
故选：A．
本题考查因式分解的意义，一提，二套，三检查，注意分解要彻底．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、100°
【解析】
由平行四边形的性质得出对角相等，邻角互补，∠A＝∠C，∠A+∠B＝180°，由∠A+∠C＝160°，得出∠A＝∠C＝80°，即可求出∠B．
【详解】
解：∵四边形ABCD是平行四边形，
∴∠A＝∠C，∠A+∠B＝180°，
∵∠A+∠C＝160°，
∴∠A＝∠C＝80°，
∴∠B＝180°﹣∠A＝100°；
故答案为：100°．
本题考查了平行四边形的性质；熟练掌握平行四边形的对角相等，邻角互补的性质是解决问题的关键．
10、-8
【解析】
把点A（a，b）分别代入一次函数y=x-1与反比例函数 ，求出a-b与ab的值，代入代数式进行计算即可．
【详解】
∵点A(a,b)是一次函数y=x+2与反比例函数的交点，
∴b=a+2,，即a−b=-2，ab=4，
∴原式=ab(a−b)=4×（-2）=-8.
反比例函数与一次函数的交点问题，对于本题我们可以先分别把点代入两个函数中，在对函数和所求的代数式进行适当变形，然后整体代入即可.
11、10cm
【解析】
求出BC，求出BF=DF，DE=AE，代入得出四边形DECF的周长等于BC+AC，代入求出即可．
【详解】
解：∵∠A=∠B，
∴BC=AC=5cm，
∵DF∥AC，
∴∠A=∠BDF，
∵∠A=∠B，
∴∠B=∠BDF，
∴DF=BF，
同理AE=DE，
∴四边形DECF的周长为：CF+DF+DE+CE=CF+BF+AE+CE=BC+AC=5cm+5cm=10cm，
故答案为10cm．
本题考查了平行线的性质，等腰三角形的性质和判定，关键是求出BF=DF，DE=AE．
12、中位数
【解析】
参赛选手要想知道自己是否能进入前6名，只需要了解自己的成绩与全部成绩的中位数的大小即可．
【详解】
解：由于总共有12个人，且他们的分数互不相同，要判断是否进入前6名，只要把自己的成绩与中位数进行大小比较．故应知道中位数的多少即可，故答案为：中位数.
本题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义．
13、4
【解析】
连接DE，交AC于点P，连接BD，由正方形的性质及对称的性质可得DE即为所求，然后运用勾股定理在RT△CDE中求解即可.
【详解】
解：连接DE，交AC于点P，连接BD．
∵点B与点D关于AC对称，
∴DE的长即为PE+PB的最小值，
∵AB＝8，E是BC的中点，
∴CE＝4，
在Rt△CDE中，
DE＝．
故答案为．
正方形的性质、对称的性质及勾股定理是本题的考点，根据题意作出辅助线并确定DE即为所求是解题的关键.
三、解答题（本大题共5个小题，共48分）
14、4a，20
【解析】
先进行二次根式的化简，然后再合并同类二次根式，最后把a的值代入进行计算即可得．
【详解】
解：原式=
=
=
当a=1时，原式=．
本题考查了二次根式的化简求值，正确化简二次根式是解题关键．
15、（1）30°；（2）①；②
【解析】
（1）由旋转的性质，得△ABD≌，则，然后证明是等边三角形，即可得到；
（2）①将绕点A逆时针旋转，使点B与点C重合，得到，连接．与（1）同理证明为等边三角形，然后利用全等三角形的判定和性质，即可得到答案；
②由解直角三角形求出，再由等边三角形的性质，即可求出答案．
【详解】
解：（1）根据题意，∵，，
∴是等腰直角三角形，
∴，
∵，
∴，
由旋转的性质，则△ABD≌，
∴，，，
∴，
∴是等边三角形，
∴，
∵，，
∴≌，
∴，
∴；
（2）①，
．
如图1，将绕点A逆时针旋转，使点B与点C重合，得到，连接．
，
，
，
，
，
．
．
，
为等边三角形，
，
，
，
，
．
②如图2，由①知，，
在中，，
．
是等边三角形，
，
，
．
本题考查了解直角三角形，旋转的性质，全等三角形的判定和性质，等边三角形的判定和性质，等腰直角三角形的性质，以及三角形的内角和定理，解题的关键是熟练掌握所学的知识，正确利用旋转模型进行解题．
16、（1）证明见解析 （2）证明见解析 （3）
【解析】
（1）利用菱形的四条边相等，可证CD=DM=CM=AD，就可得到△CDM是等边三角形，再利用等边三角形的三个角都是60°，就可求出∠M的度数；
（2）过点E作EG∥CM交CD的延长线于点G，可得到∠G=∠HCF，先证明△EDG是等边三角形，结合已知条件证明EG=CF，利用AAS证明△EGH≌△FCH，再根据全等三角形的对应边相等，可证得结论；
（3）设BD，EF交于点N，根据前面的证明可知BD=CD=AB=3，∠M=∠CDM=60°，DE=CF，再利用垂直的定义及三角形内角和定理可求出∠HED，∠EHD的度数，从而利用等腰三角形的判定和性质，可证得ED=DH=CF，可推出CD=3DH，就可求出DH的长，然后利用解直角三角形分别求出BN，NH的长，再利用勾股定理就可求出BH的长.
【详解】
（1）证明：∵ 四边形ABCD和四边形BCMD都是菱形，
∴BC=CD=AD，BC=DM=CM
∴CD=DM=CM=AD，
∴△CDM是等边三角形，
∴∠M=60°。
（2）解： 如图2，过点E作EG∥CM交CD的延长线于点G，
∴∠G=∠HCF=60°，∠GED=∠M=60°，
∴∠G=∠GED=∠EDG=60°，
∴△EDG是等边三角形
∴EG=DE；
∵AD=CM，AE=MF，
∴DE=CF，
∴EG=CF；
在△EGH和△FCH中，
∴△EGH≌△FCH（AAS）
∴EH=FH.
（3）解： 如图3，设BD，EF交于点N，
由（1）（2）的证明过程可知BD=CD=AB=3，∠M=∠CDM=60°，DE=CF，
∵EF⊥CM，
∴∠EFM=90°，
∴∠HED=90°-60°=30°，
∠CDM=∠HED+∠EHD=60°
∴∠EHD=60°-30°=30°=∠HED=∠CHF
∴ED=DH=CF，
在R△CHF中，∠CHF=30°
∴CH=2CH=2DH，
∴CD=CH+DH=3DH=3
解之：DH=CF=1
∵菱形CBDM，EF⊥CM
∴BD∥CM
∴EF⊥BD；
∴∠DNH=∠BNH=90°，
在Rt△DHN中，∠DHN=30°，DH=1
∴DN=DHsin∠30°=，
NH=DHcs30°=；
∴BN=BD-DN=3-=，
在Rt△BHN中，
BH=.
本题是四边形综合题目，考查了菱形的性质、等边三角形的判定与性质、相似三角形的判定与性质、平行线的性质、勾股定理、含30°角的直角三角形的性质等知识；本题综合性强，熟练掌握等边三角形的判定与性质是解题的关键．
17、应聘者将被录用
【解析】
根据加权平均数的定义分别计算A、B两人的成绩，比较即得答案．
【详解】
解：的成绩：，
的成绩：，
∵，
∴应聘者将被录用．
本题考查了加权平均数的计算，属于基础题型，正确理解题意、熟练掌握计算方法是解答的关键．
18、（1）见解析；（1）BD＝DE＝CE的数量关系时，△CD′E是正三角形；（3）见解析．
【解析】
（1）根据轴对称的性质得到AD=AD`，即可证明△ABD≌△ACD′
（1）由（1）可得∠BAD＝∠CAD′，∠B＝∠ACD′，再根据轴对称的性质得到∠EAD′+∠CAE＝∠BAD+∠CAE＝∠DAE＝∠BAC＝60°，得到△CD′E是正三角形，即可解答
（3）利用勾股定理即可解答
【详解】
（1）证明：∵△ADE与△AD′E是关于AE的轴对称图形，
∴AD＝AD′，
在△ABD和△ACD′中， ，
∴△ABD≌△ACD′（SSS）；
（1）解：∵△ABD≌△ACD′，
∴∠BAD＝∠CAD′，∠B＝∠ACD′，
∵△ADE与△AD′E是关于AE的轴对称图形，
∴∠DAE＝∠EAD′，DE＝ED′，
∴∠EAD′+∠CAE＝∠BAD+∠CAE＝∠DAE＝∠BAC＝60°，
∵△CD′E是正三角形，
∴CE＝CD′＝ED′，
∵BD＝CD′，DE＝ED′，
∴BD＝DE＝CE；
（3）证明：∵∠BAC＝90°，AB＝AC，
∴∠B＝∠ACB＝∠ACD′＝45°，
∴∠ECD′＝90°，
∴ED′1＝CD′1+EC1，
∵BD＝CD′，DE＝ED′，
∴DE1＝BD1+EC1．
此题考查全等三角形的判定与性质，勾股定理，等边三角形的判定与性质，解题关键在于利用全等三角形的性质进行解答
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
由x3+8=0，得x3=-8，所以x=-1．
【详解】
由x3+8=0，得
x3=-8，
x=-1，
故答案为：x=-1．
本题考查了立方根，正确理解立方根的意义是解题的关键．
20、 (a＋2)(a－2)；
【解析】
有两项，都能写成完全平方数的形式，并且符号相反，可用平方差公式展开．
【详解】
解：a2-4=（a+2）（a-2）．
故答案为：(a＋2)(a－2)．
考点：因式分解-运用公式法．
21、1:1
【解析】
试题分析：当AB：AD＝1：1时，四边形MENF是正方形，
理由是：∵AB：AD＝1：1，AM＝DM，AB＝CD，
∴AB＝AM＝DM＝DC，
∵∠A＝∠D＝90°，
∴∠ABM＝∠AMB＝∠DMC＝∠DCM＝45°，
∴∠BMC＝90°，
∵四边形ABCD是矩形，
∴∠ABC＝∠DCB＝90°，
∴∠MBC＝∠MCB＝45°，
∴BM＝CM，
∵N、E、F分别是BC、BM、CM的中点，
∴BE＝CF，ME＝MF，NF∥BM，NE∥CM，
∴四边形MENF是平行四边形，
∵ME＝MF，∠BMC＝90°，
∴四边形MENF是正方形，
即当AB：AD＝1：1时，四边形MENF是正方形，
故答案为：1：1．
点睛：本题考查了矩形的性质、正方形的判定、三角形中位线定理等知识，熟练应用正方形的判定方法是解题关键．
22、①③④
【解析】
根据已知先判断△ABC≌△EFA，则∠AEF=∠BAC，得出EF⊥AC，由等边三角形的性质得出∠BDF=30°，从而证得△DBF≌△EFA，则AE=DF，再由FE=AB，得出四边形ADFE为平行四边形而不是菱形，根据平行四边形的性质得出AD=4AG，从而得到答案．
【详解】
解：∵△ACE是等边三角形，
∴∠EAC=60°，AE=AC，
∵∠BAC=30°，
∴∠FAE=∠ACB=90°，AB=2BC，
∵F为AB的中点，
∴AB=2AF，
∴BC=AF，
∴△ABC≌△EFA，
∴FE=AB，
∴∠AEF=∠BAC=30°，
∴EF⊥AC，故①正确，
∵EF⊥AC，∠ACB=90°，
∴HF∥BC，
∵F是AB的中点，
∴HF=BC，
∵BC=AB，AB=BD，
∴HF=BD，故④说法正确；
∵AD=BD，BF=AF，
∴∠DFB=90°，∠BDF=30°，
∵∠FAE=∠BAC+∠CAE=90°，
∴∠DFB=∠EAF，
∵EF⊥AC，
∴∠AEF=30°，
∴∠BDF=∠AEF，
∴△DBF≌△EFA（AAS），
∴AE=DF，
∵FE=AB，
∴四边形ADFE为平行四边形，
∵AE≠EF，
∴四边形ADFE不是菱形；
故②说法不正确；
∴AG=AF，
∴AG=AB，
∵AD=AB，
则AD=4AG，故③说法正确，
故答案为①③④．
考点：菱形的判定；等边三角形的性质；含30度角的直角三角形．
23、y2【解析】
解：反比例函数当x<0时为减函数且y<0，由x1当x>0时，y>0，由x3>0，所以y3>0
综上所述可得y2故答案为：y2二、解答题（本大题共3个小题，共30分）
24、（1）50，30；（2）72；（3）270名学生.
【解析】
（1）根据其他的人数和所占的百分比即可求得m的值，从而可以求得n的值，求得喜爱文学的人数，从而可以将条形统计图补充完整；
（2）根据扇形统计图中的数据可以求得“艺术”所对应的扇形的圆心角度数；
（3）根据统计图中的数据可以估计该校900名学生中有多少学生最喜欢科普类图书．
【详解】
解：（1） ，
文学有： ，
补全的条形统计图如右图所示；
故答案为50，30；
（2）由题意可得，“艺术”所对应的扇形的圆心角度数是：，
故答案为72；
（3）由题意可得，，
即该校900名学生中有270名学生最喜欢科普类图书．
本题考查了条形统计图和扇形统计图，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
25、
【解析】
根据矩形的性质求出△AOB的面积等于矩形ABCD的面积的，求出△AOB的面积，再分别求出△ABO1、△ABO2、△ABO3、△ABO4的面积，求出平行四边形的面积，然后再观察发现规律进行解答．
【详解】
解：∵四边形ABCD是矩形，
∴AO＝CO，BO＝DO，DC∥AB，DC＝AB，
∴S△ADC＝S△ABC＝S矩形ABCD＝×20＝10，
∴S△AOB＝S△BCO＝S△ABC＝×10＝5，
∴S△ABO1＝S△AOB＝×5＝，
∴S△ABO2＝S△ABO1＝，
S△ABO3＝S△ABO2＝，
S△ABO4＝S△ABO3＝，
∴S平行四边形AO4C5B＝2S△ABO4＝2×＝，
∴平行四边形的面积为：，
故答案为：，.
本题考查了三角形的面积，矩形的性质，平行四边形的性质的应用，解此题的关键是能根据求出的结果得出规律，注意：等底等高的三角形的面积相等．
26、ME＝NF且ME∥NF，理由见解析
【解析】
利用SAS证得△BME≌△DNF后即可证得结论．
【详解】
证明：ME＝NF且ME∥NF．理由如下：
∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠EBM＝∠FDN，AB＝CD，
∵AM＝CN，
∴MB＝ND，
∵BE＝DF，
∴BF＝DE，
∵在△BME和△DNF中
，
∴△BME≌△DNF（SAS），
∴ME＝NF，∠MEB＝∠NFD，
∴∠MEF＝∠BFN．
∴ME∥NF．
∴ME＝NF且ME∥NF．
此题主要考查了平行四边形的性质以及全等三角形的判定与性质，熟练掌握全等三角形的判定方法是解题关键．
题号
一
二
三
四
五
总分
得分
批阅人