

【专项练习】全套专题数学2023-2024教科院三 中考九年级下学期期末数学试卷不含解析
展开注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
6.本学科试卷共25个小题,考试时量120分钟,满分120分.
一、选择题(在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项.本大题共10个小题,每小题3分,共30分)
1.的绝对值是( )
A.2B.0C.D.
2.如图是由4个相同的小立方体搭成的几何体如图所示,则它的左视图是( )
A.B.C.D.
3.下列运算正确的是( )
A.B.C.D.
4.一元二次方程的根的情况是( )
A.有两个相等的实数根B.有两个不相等的实数根
C.只有一个实数根D.没有实数根
(第5题图) (第6题图) (第9题图) (第10题图)
5.如图,在菱形ABCD中,对角线AC与BD相交于点O,OE//DC交BC于点E.若,则OE的长为( )
A.6cmB.4cmC.3cmD.2cm
6.将等腰直角三角形纸片和长方形纸片按如图方式叠放.若,则∠2的度数为( )
A.48°B.20°C.23°D.17°
7.《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数几何?译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,如果设有x人,则可列方程为( )
A.B.C.D.
8.下列说法正确的是( )
A.调查“神舟十六号”载人飞船零件的质量,应采用全面调查的方式
B.数据3,5,4,1,2的中位数是4 C.“清明时节雨纷纷”是必然事件
D.甲、乙两名射击运动员10次射击成绩(单位:环)的平均数相等,方差分别为,,则乙的成绩比甲的稳定
9.如图,已知四边形ABDC内接于⊙O,,则∠BOC的度数为( )
A.130°B.120°C.110°D.100°
10.如图,在Rt△ABC中,,,,D是线段AB上一点(点D不与A,B重合),过点D作DE⊥BC,交BC于点E,F为CE中点,连接CD,得到以下四个结论:①当时,;②当DE垂直平分线段BF时,;③当时,;④当D为AB的中点时,△DCE面积最大.其中正确的是( )
A.①②③B.①③④C.①②④D.②③④
二、填空题(本大题共6个小题,每小题3分,共18分)
11.分解因式:__________.
12.若扇形的圆心角为90°,半径为6,则该扇形的弧长为__________.
(第13题图) (第14题图) (第15题图) (第16题图)
13.如图,直线和直线相交于,则关于x的不等式的解集为__________.
14.如图,电路上有3个开关S1、S2、S3和1个小灯泡L,任意闭合电路上2个开关,小灯泡发光的概率为__________.
15.如图,⊙O的半径为4,△ABC是⊙O的内接三角形,半径OD⊥BC于点E.当时,BE的长是__________.
16.如图,点M是反比例函数图象上的一点,过点M作MN⊥x轴于点N,点P在y轴上.若△MNP的面积是3,则__________.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
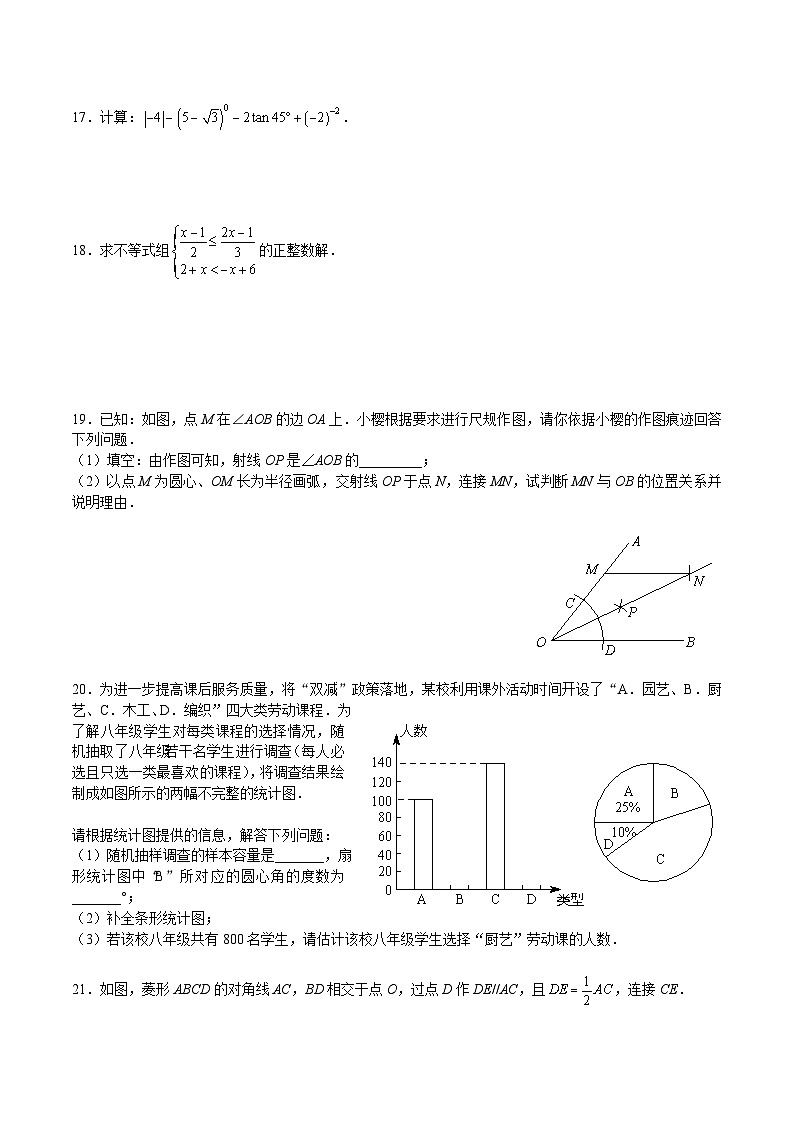
17.计算:.
18.求不等式组的正整数解.
19.已知:如图,点M在∠AOB的边OA上.小樱根据要求进行尺规作图,请你依据小樱的作图痕迹回答下列问题.
(1)填空:由作图可知,射线OP是∠AOB的_________;
(2)以点M为圆心、OM长为半径画弧,交射线OP于点N,连接MN,试判断MN与OB的位置关系并说明理由.
20.为进一步提高课后服务质量,将“双减”政策落地,某校利用课外活动时间开设了“A.园艺、B.厨艺、C.木工、D.编织”四大类劳动课程.为了解八年级学生对每类课程的选择情况,随机抽取了八年级若干名学生进行调查(每人必选且只选一类最喜欢的课程),将调查结果绘制成如图所示的两幅不完整的统计图.
请根据统计图提供的信息,解答下列问题:
(1)随机抽样调查的样本容量是_______,扇形统计图中“B”所对应的圆心角的度数为_______°;
(2)补全条形统计图;
(3)若该校八年级共有800名学生,请估计该校八年级学生选择“厨艺”劳动课的人数.
21.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE//AC,且,连接CE.
(1)求证:四边形OCED为矩形;
(2)连接AE.若,,求菱形ABCD的面积.
22.第19届亚运会于2023年9月23日至10月8日在杭州举行,作为一个国际性的盛事,亚运会为杭州城市的发展带来巨大的机遇.杭州街头增添了许多令人惊叹的高科技设施.在准备过程中,政府计划购买A,B两种型号的能为手机无线充电的智能太阳能座椅.已知购买1套A型座椅和1套B型座椅需5500元,购买2套A型座椅和1套B型座椅需8500元.
(1)求A,B型座椅的单价分别是多少元;
(2)政府计划购买两种智能太阳能座椅共80台,要求A型座椅数量不少于B型座椅数量的.设购买a台A型座椅,购买A,B型两种座椅的总费用为w元,求w关于a的函数解析式,并求出购买两种座椅的总费用最少需要多少元.
23.如图,在Rt△ABC中,,,点D是边BC上一点,BE⊥AB交AD的延长线于点E,点F是AE的中点,连接CF,BF.
(1)求证:△ACF≌△BCF;
(2)若,,求BF的长.
24.如图,四边形ABCD内接于⊙O,对角线AC,BD交于点E,连接OE.若AC⊥BD,⊙O的半径为r,.
(1)若,求证:OE平分∠AEB;
(2)试用含r,m的式子表示的值;
(3)记△ADE,△BCE,△ABE,△CDE的面积分别为S1,S2,S3,S4,当时,求证:.
25.对某一个函数给出如下定义:如果函数的自变量x与函数值y满足:当时,(m,n为实数,且),我们称这个函数在m→n上是“民主函数”.比如:函数在→2上是“民主函数”.理由:∵由,得.∵,∴,解得,∴,∴是“民主函数”.
(1)反比例函数是2→3上的“民主函数”吗?请判断并说明理由;
(2)若一次函数在m→n上是“民主函数”,求此函数的解析式(可用含m,n的代数式表示);
(3)若抛物线(,)在1→3上是“民主函数”,且在上的最小值为4a,设抛物线与直线交于A,B点,与y轴相交于C点.若△ABC的内心为G,外心为M,试求MG的长.
【专项练习】全套专题数学2023-2024教科院四 中考九年级下学期期末数学试卷不含解析: 这是一份【专项练习】全套专题数学2023-2024教科院四 中考九年级下学期期末数学试卷不含解析,共7页。试卷主要包含了分式方程的解是等内容,欢迎下载使用。
【专项练习】全套专题数学2023-2024教科院六 中考九年级下学期期末数学试卷不含解析: 这是一份【专项练习】全套专题数学2023-2024教科院六 中考九年级下学期期末数学试卷不含解析,共7页。
【专项练习】全套专题数学2023-2024教科院八中考九年级下学期期末数学试卷不含解析: 这是一份【专项练习】全套专题数学2023-2024教科院八中考九年级下学期期末数学试卷不含解析,共7页。












