+江苏省南京师范大学附属中学树人学校2024-2025学年八年级上学期第一次月考数学试卷

这是一份+江苏省南京师范大学附属中学树人学校2024-2025学年八年级上学期第一次月考数学试卷，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）下列图形中，不是轴对称图形的是（ ）
A．B．
C．D．
2．（3分）如图，△ABC≌△DEF，若∠A=100°，∠F=47°，则∠E的度数为（ ）
A．100°B．53°C．47°D．33°
3．（3分）如图△ABC≌△DEF，点D、E在直线AB上，BE=4，AE=1，则DE的长为（ ）
A．5B．4C．3D．2
4．（3分）等腰三角形的一边为4cm，一边为3cm，则此三角形的周长是（ ）
A．10cmB．11cm
C．6cm或8cmD．10cm或11cm
5．（3分）A、B、C三名同学玩“抢凳子”游戏．他们所站的位围成一个△ABC，在他们中间放一个木凳，谁先抢到凳子谁获胜，为保证游戏公平，则凳子应放的最适当的位置是在△ABC的（ ）
A．三边垂直平分线的交点
B．三边中线的交点
C．三个内角角平分线的交点
D．三边高的交点
6．（3分）如图1，已知三角形纸片ABC，AB=AC，∠A=50°，将其折叠，如图2，使点A与点B重合，折痕为ED，点E，D分别在AB，AC上，那么∠DBC的度数为（ ）
A．10°B．15°C．20°D．30°
7．（3分）如图，已知△ABC的周长是36cm,∠ABC和∠ACB的角平分线交于点O，OD⊥BC于点D，若OD=3cm,则△ABC的面积是（ ）
A．48cm2B．54cm2C．60cm2D．66cm2
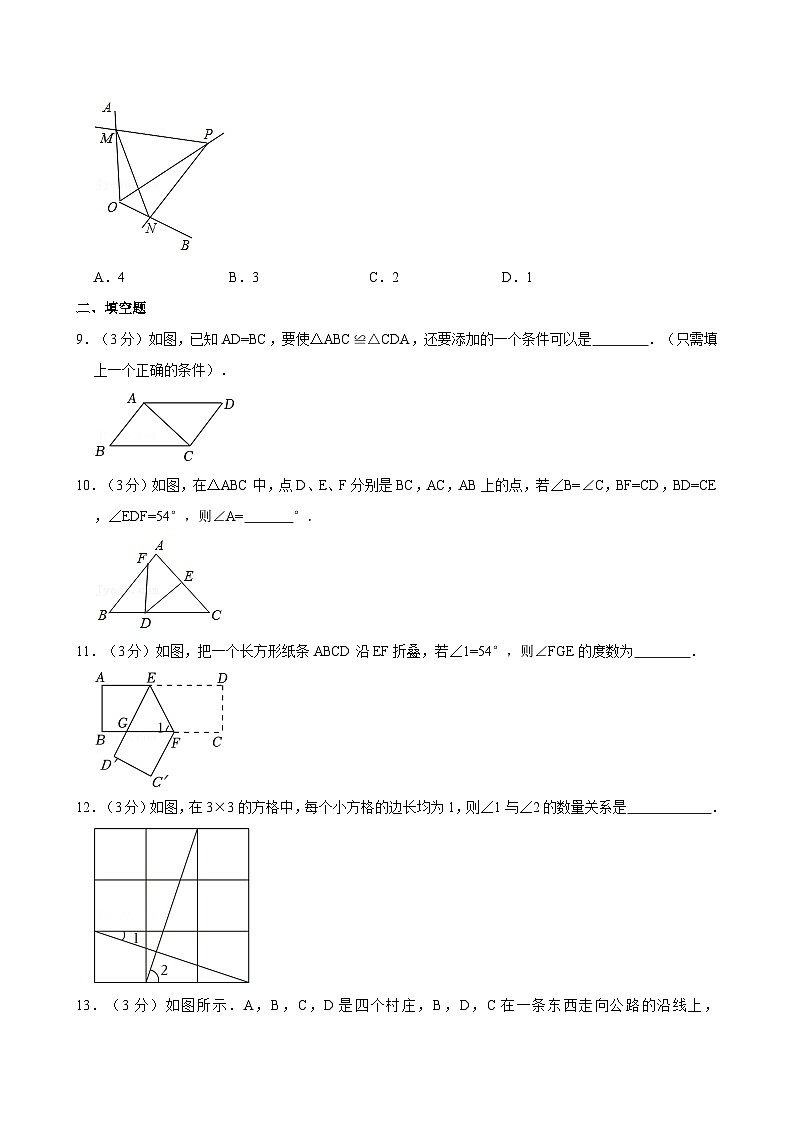
8．（3分）如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（ ）
A．4B．3C．2D．1
二、填空题
9．（3分）如图，已知AD=BC，要使△ABC≌△CDA，还要添加的一个条件可以是 ．（只需填上一个正确的条件）．
10．（3分）如图，在△ABC中，点D、E、F分别是BC，AC，AB上的点，若∠B=∠C，BF=CD，BD=CE，∠EDF=54°，则∠A= °．
11．（3分）如图，把一个长方形纸条ABCD沿EF折叠，若∠1=54°，则∠FGE的度数为 ．
12．（3分）如图，在3×3的方格中，每个小方格的边长均为1，则∠1与∠2的数量关系是 ．
13．（3分）如图所示．A，B，C，D是四个村庄，B，D，C在一条东西走向公路的沿线上，BD=1km,DC=1km,村庄AC，AD间也有公路相连，且公路AD是南北走向，AC=3km,只有AB之间由于间隔了一个小湖，所以无直接相连的公路．现决定在湖面上造一座斜拉桥，测得AE=1.2km,BF=0.7km.试求建造的斜拉桥长至少有 km．
14．（3分）如图，在△ABC中，AB=4，AC=5.5，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC分别交AB、AC于点M、N，则△AMN的周长为 ．
15．（3分）如图，△ABC的面积为12cm2，AP垂直∠B的平分线BP于点P，则△PBC的面积为 cm2．
16．（3分）如图，在射线OA，OB上分别截取OA1＝OB1，连接A1B1，在B1A1、B1B上分别截取B1A2＝B1B2，连接A2B2…按此规律作下去，若∠A1B1O＝α，则∠A2023B2023O＝ ．
17．（3分）如图，AB=7cm,∠CAB=∠DBA=60°，AC=5cm,点P在线段AB上以2cm/s的速度由点A向点B运动，同时点Q在射线BD上运动，当点P运动结束时，点Q随之结束运动当点PQ运动到某处时有△ACP与△BPQ全等，则Q的运动速度是 cm/s．
18．（3分）如图，在△ABC中，BA=BC，BD平分∠ABC，交AC于点D，点M、N分别为BD、BC上的动点，若BC=4，△ABC的面积为6，则CM+MN的最小值为 ．
三、解答题
19．如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
（1）在图中画出与△ABC关于直线l成轴对称的△A′B′C′．
（2）△ABC的面积为 ．
（3）在直线l上找一点P（在答题纸上图中标出），使PB+PC的长最短．
20．如图，已知B，E，C，F在同一条直线上，AB=DE，AC=DF，BE=CF．AC与DE交于点G，
（1）求证△ABC≌△DEF；
（2）若∠B=50°，∠ACB=60°，求∠EGC的度数．
21．麒麟某数学兴趣小组的同学用数学知识测一池塘的长度，他们所绘如图，点B，F，C，E在直线l上（点F，C之间不能直接测量，为池塘的长度），点A，D在l的异侧，且AB∥DE，∠A=∠D，测得AB=DE．
（1）求证：△ABC≌△DEF；
（2）若BE=100m,BF=30m,求池塘FC的长．
22．如图，四边形ABCD中，BC=CD，AC=DE，∠B=∠DCE=90°，AC与DE相交于点F．
（1）求证：△ABC≌△ECD；
（2）判断线段AC与DE的位置关系，并说明理由．
23．如图，在△ABC中，DM、EN分别垂直平分AC和BC，交AB于M、N两点，DM与EN相交于点F．
（1）若△CMN的周长为15cm,求AB的长；
（2）若∠MFN=70°，求∠MCN的度数．
24．如图，已知△ABC，点P为∠BAC的平分线上一点，PE⊥AB，PF⊥AC，垂足分别为E、F．
（1）求证：PE=PF；
（2）若BE=CF，求证：点P在BC的垂直平分线上．
25．如图，已知△ABC（AC＜AB＜BC），请用无刻度的直尺和圆规，完成下列作图（不写作法，保留作图痕迹）．
（1）如图1，在AB边上寻找一点M，使∠AMC=∠ACB；
（2）如图2，在BC边上寻找一点N，使得NA+NB=BC．
26．如图甲，已知在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．
（1）说明△ADC≌△CEB．
（2）说明AD+BE=DE．
（3）已知条件不变，将直线MN绕点C旋转到图乙的位置时，若DE=3、AD=5.5，则BE= ．
27．【概念学习】
规定①：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“形似三角形”．
规定②：从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“形似三角形”，我们把这条线段叫做这个三角形的“等腰分割线”．
【概念理解】
（1）如图1，在△ABC中，∠A=36°，AB=AC，CD平分∠ACB，则△CBD与△ABC （填“是”或“不是”）互为“形似三角形”．
（2）如图2，在△ABC中，CD平分∠ACB，∠A=36°，∠B=48°．求证：CD为△ABC的等腰分割线；
【概念应用】
（3）在△ABC中，∠A=45°，CD是△ABC的等腰分割线，直接写出∠ACB的度数．
28．在△ABC中，AB=AC，BC=8，点M从点B出发沿射线BA移动，同时点N从点C出发沿线段AC的延长线移动，点M，N移动的速度相同，MN与BC相交于点D．
（1）如图1，过点M作ME∥AC，交BC于点E；
①图中与BM相等的线段有 、 ；
②求证：△DME≌△DNC；
（2）如图2，若∠A=60°，当点M移动到AB的中点时，求CD的长度；
（3）如图3，过点M作MF⊥BC于点F，在点M从点B向点A（点M不与点A，B重合）移动的过程中，线段BF与CD的和是否保持不变？若保持不变，请直接写出BF与CD的长度和；若改变，请说明理由．
2024-2025学年江苏省南京师大附中树人学校八年级（上）第一次月考数学试卷
参考答案与试题解析
一、选择题
1．【答案】C
2．【答案】D
3．【答案】A
4．【答案】D
5．【答案】A
6．【答案】B
7．【答案】B
8．【答案】B
二、填空题
9．【答案】AB＝CD．
10．【答案】72．
11．【答案】72°．
12．【答案】∠1+∠2＝90°．
13．【答案】6.1．
14．【答案】9.5．
15．【答案】6．
16．【答案】．
17．【答案】2或．
18．【答案】3
三、解答题
19．【答案】（1）如图所示，△A′B′C′即为所求；
（2）2×4﹣﹣×6×3﹣﹣5＝，
故答案为：；
（3）连接BC′，交l于P．
20．【答案】（1）证明：∵BE＝CF，
∴BE+EC＝CF+EC，即BC＝EF，
∵AB＝DE，BC＝EF，
∴△ABC≌△DEF（SSS）；
（2）解：如图，
由（1）知，△ABC≌△DEF（SSS），
∴∠B＝∠DEF，
∴AB∥DE，
∴∠EGC＝∠A，
∵∠B＝50°，∠ACB＝60°，
∴∠A＝180°﹣∠B﹣∠ACB＝70°，
∴∠EGC＝70°．
21．【答案】（1）证明：∵AB∥DE，
∴∠ABC＝∠DEF，
在△ABC与△DEF中，
∴△ABC≌DEF（ASA）；
（2）解：∵△ABC≌△DEF，
∴BC＝EF
∴BF+FC＝EC+FC，
∴BF＝EC，
∵BE＝100m，BF＝30m，
∴FC＝100﹣30﹣30＝40m．
答：FC的长是40m．
22．【答案】（1）证明：在Rt△ABC和Rt△ECD中，
，
∴Rt△ABC≌Rt△ECD（HL），
（2）解：AC⊥DE．理由如下：
∵△ABC≌△ECD，
∴∠BCA＝∠CDE，
∵∠B＝∠DCE＝90°，
∴∠BCA+∠ACD＝90°，
∴∠CDE+∠ACD＝90°，
∴∠DFC＝180°﹣（∠CDE+∠ACD）＝90°，
∴AC⊥DE．
23．【答案】解：（1）∵DM、EN分别垂直平分AC和BC，
∴AM＝CM，BN＝CN，
∴△CMN的周长＝CM+MN+CN＝AM+MN+BN＝AB，
∵△CMN的周长为15cm，
∴AB＝15cm；
（2）∵∠MFN＝70°，
∴∠MNF+∠NMF＝180°﹣70°＝110°，
∵∠AMD＝∠NMF，∠BNE＝∠MNF，
∴∠AMD+∠BNE＝∠MNF+∠NMF＝110°，
∴∠A+∠B＝90°﹣∠AMD+90°﹣∠BNE＝180°﹣110°＝70°，
∵AM＝CM，BN＝CN，
∴∠A＝∠ACM，∠B＝∠BCN，
∴∠MCN＝180°﹣2（∠A+∠B）＝180°﹣2×70°＝40°．
24．24．【答案】（1）见解析；
（2）见解析．
【解答】证明：（1）∵点P为∠BAC的平分线上一点
∴∠BAP＝∠FAP
∵PE⊥AB，PF⊥AF
∴∠PEA＝∠PFA＝90°
在△APE和△APF中
∴△APE≌△APF（AAS）
∴PE＝PF
（2）连接PB、PC
由（1）可得：∠BEP＝∠CFP＝90°
又∵PE＝PF，BE＝CF
∴△BPE≌△CPF（SAS）
∴BP＝CP
∴点P在BC的垂直平分线上
25．【答案】见解答．
【解答】解：（1）如图1，点M为所作；
（2）如图2，点N为所作．
26．【答案】见试题解答内容
【解答】（1）证明：∵AD⊥MN，BE⊥MN，
∴∠ADC＝∠BEC＝90°，
∵∠ACB＝90°，
∴∠ACD+∠BCE＝90°，∠DAC+∠ACD＝90°，
∴∠DAC＝∠BCE，
∵∠ADC＝∠BEC，AC＝BC，
∴△ADC≌△CEB．
（2）证明：由（1）知：△ADC≌△CEB，
∴AD＝CE，CD＝BE，
∵DC+CE＝DE，
∴AD+BE＝DE．
（3）证明：∵BE⊥BC，AD⊥CE，
∴∠ADC＝∠BEC＝90°，
∴∠EBC+∠ECB＝90°，
∵∠ACB＝90°，
∴∠ECB+∠ACE＝90°，
∴∠ACD＝∠EBC，
在△ADC和△CEB中
∵，
∴△ADC≌△CEB，
∴AD＝CE，CD＝BE，
∵DE＝3、AD＝5.7，
∴BE＝CD＝CE﹣DE＝2.5．
故答案为：4.5．
27．【答案】见试题解答内容
【解答】（1）解：∵∠A＝36°，AB＝AC，
∴∠ABC＝∠ACB＝72°，
∵CD平分∠ACB，
∴∠BCD＝36°，
∵∠ABC＝72°，
∴∠BDC＝72°，
∴△CBD和△ABC互为“形似三角形”，
故答案为：是；
（2）证明：∵∠A＝36°，∠B＝48°，
∴∠ACB＝180°﹣36°﹣48°＝96°，
∵CD平分∠ACB，
∴＝，
∴∠BCD＝∠B，
∴△BCD是等腰三角形，∠ACD＝∠A＝36°，∠ADC＝∠ACB＝96°，
∴CD为△ABC的等腰分割线；
（3）解：（Ⅰ）当△ACD是等腰三角形时，
①如图1，
当AD＝CD时，则∠ACD＝∠A＝45°，
∴∠BDC＝∠A+∠ACD＝90°，
此时∠BCD＝∠A＝45°，
∴∠ACB＝90°（不合题意舍去）；
②如图3，
当AC＝AD时，则＝67.5°，
此时∠BCD＝∠A＝45°，
∴∠ACB＝45°+67.4°＝112.5°；
③当AC＝CD时，这种情况不存在；
（Ⅱ）当△BCD是等腰三角形时，
①如图3，
当CD＝DB时，∠B＝∠BCD＝∠ACD，
∴∠BDC＝∠ACD+∠A＝∠ACD+45°，
∵∠BDC+∠B+∠BCD＝180°，
∴∠ACD+45°+∠ACD+∠ACD＝180°，
∴∠ACD＝45°，
∴∠ACB＝∠ACD+∠BCD＝6×45°＝90°；
②如图4，
当BC＝BD，∠B＝∠ACD时，
∴∠BCD＝∠BDC＝∠ACD+∠A＝∠ACD+45°，
由∠B+2∠BDC＝180°，得∠ACD+2（∠ACD+45°）＝180°，
∴∠ACD＝30°，
∴∠ACB＝∠ACD+∠BCD＝45°+2×30°＝105°；
③当CD＝CB时，这种情况不存在；
综上所述：∠ACB＝112.5°或105°．
28．【答案】（1）①EM；CN； ②见解析过程；
（2）CD的长度为2；
（3）线段BF与CD的和是保持不变，BF+CD＝4．
【解答】（1）①解：∵点M，N同时移动且移动的速度相同，
∴BM＝CN，
∵AB＝AC，
∴∠B＝∠ACB，
又∵ME∥AC，
∴∠N＝∠DME，∠ACB＝∠MEB，
∴∠MEB＝∠B，
∴BM＝ME，
故答案为：EM；CN；
②证明：∵BM＝ME，BM＝CN，
∴ME＝CN，
在△DME和△DNC中，
，
∴△DME≌△DNC（AAS）；
（2）解：过点M作ME∥AC，交BC于点E
∵∠A＝60°，AB＝AC，
∴△ABC是等边三角形，
∴∠B＝∠ACB＝60°，
∵ME∥AC，
∴∠BEM＝∠ACB＝60°，
由（1）可知：BM＝ME＝CN，
∴△BEM是等边三角形，
∴BE＝BM，
∵M是AB的中点，
∴，
∴BE＝CE＝4，
由（1）可知：△DME≌△DNC，
∴DE＝CD，
∴，
∴CD的长度为3；
（3）解：线段BF与CD的和是保持不变，理由如下：
由（1）可知：BM＝ME，
∵MF⊥BE，
∴BF＝EF，
由（1）可知：△DME≌△DNC，
∴DE＝DC，
∴BF+CD＝BC＝4．