2024-2025学年内蒙古鄂托克旗九上数学开学监测试题【含答案】

这是一份2024-2025学年内蒙古鄂托克旗九上数学开学监测试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）已知一次函数的图象过点（0，3），且与两坐标轴围成的三角形的面积为3，则这个一次函数的表达式为（ ）
A．y＝1.5x＋3B．y＝-1.5x＋3
C．y＝1.5x＋3或y＝-1.5x＋3D．y＝1.5x-3或y＝-1.5x-3
2、（4分）下列各式成立的是（ ）
A．B．C．D．
3、（4分）如图，在矩形ABCD中，AB＝8，AD＝6，过点D作直线m∥AC，点E、F是直线m上两个动点，在运动过程中EF∥AC且EF＝AC，四边形ACFE的面积是( )
A．48B．40C．24D．30
4、（4分）下列二次根式化简的结果正确的是（ ）
A．B．C．D．
5、（4分）如图，在矩形中，对角线相交于点，且，则图中长度为3的线段有（ ）
A．2条B．4条C．5条D．6条
6、（4分）如图，以正方形ABCD的边AB为一边向外作等边△ABE，则∠BED的度数为（ ）
A．55°B．45°C．40°D．42.5°
7、（4分）小强和小华两人玩“剪刀、石头、布”游戏，随机出手一次，则两人平局的概率为（ ）
A．B．C．D．
8、（4分）下列根式是最简二次根式的是（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图,正方形的边长为5，，连结，则线段的长为________．

10、（4分）计算：（﹣）2＝_____．
11、（4分）若数据8，9，7，8，x，3的平均数是7，则这组数据的众数是________．
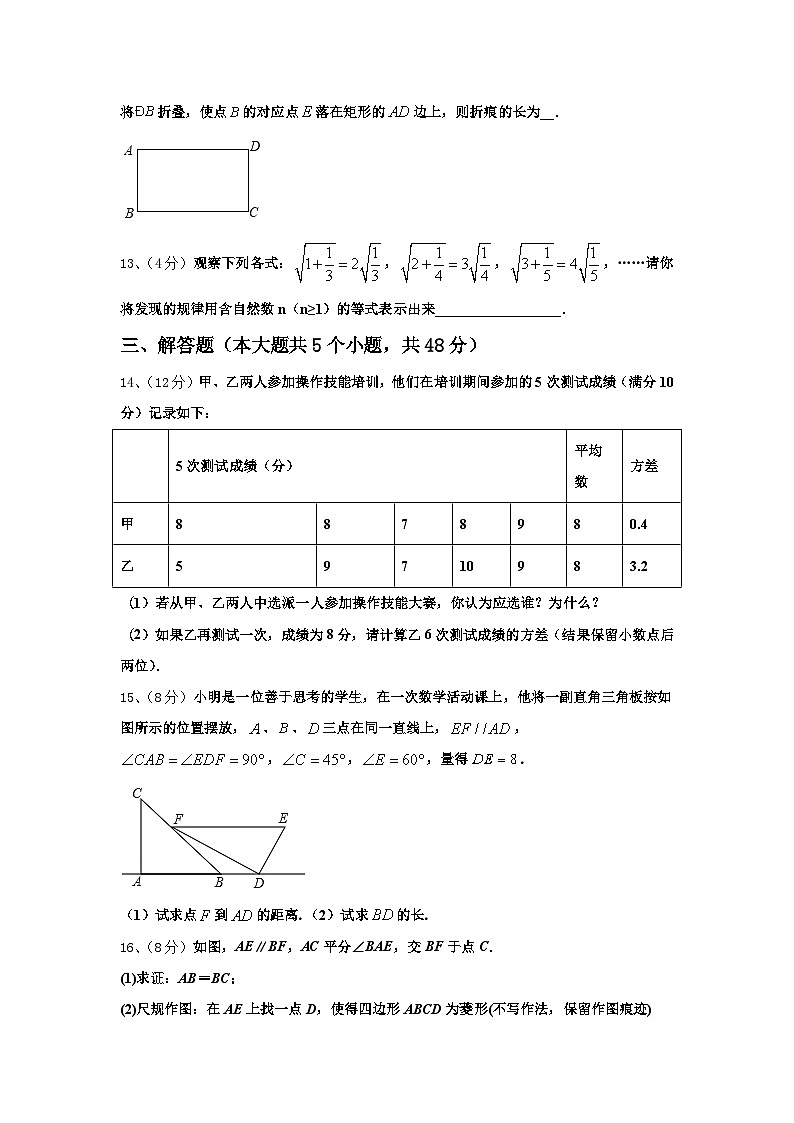
12、（4分）如图，已知在矩形中，，，沿着过矩形顶点的一条直线将折叠，使点的对应点落在矩形的边上，则折痕的长为__．
13、（4分）观察下列各式：，，，……请你将发现的规律用含自然数n（n≥1）的等式表示出来__________________．
三、解答题（本大题共5个小题，共48分）
14、（12分）甲、乙两人参加操作技能培训，他们在培训期间参加的5次测试成绩（满分10分）记录如下：
（1）若从甲、乙两人中选派一人参加操作技能大赛，你认为应选谁？为什么？
（2）如果乙再测试一次，成绩为8分，请计算乙6次测试成绩的方差（结果保留小数点后两位）．
15、（8分）小明是一位善于思考的学生，在一次数学活动课上，他将一副直角三角板按如图所示的位置摆放，、、三点在同一直线上，，，，，量得.
（1）试求点到的距离.（2）试求的长.
16、（8分）如图，AE∥BF，AC平分∠BAE，交BF于点C．
(1)求证：AB＝BC；
(2)尺规作图：在AE上找一点D，使得四边形ABCD为菱形(不写作法，保留作图痕迹)
17、（10分）某高速公路要对承建的工程进行招标，现在甲、乙两个工程队前来投标，根据两队的申报材料估计：若甲、乙两队合作，24天可以完成；若由甲队单独做20天后，余下的工程由乙队做，还需40天完成，求甲、乙两队单独完成这项工程各需多少天？
18、（10分）如图，在中，，，点，分别是，上的点，且，连接交于点.
（1）求证：.
（2）若，延长交的延长线于点，当时，求的长.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）二次根式有意义的条件是______________.
20、（4分）如图，已知反比例函数的图象经过点，若在该图象上有一点，使得，则点的坐标是_______.
21、（4分）将矩形ABCD折叠，使得对角线的两个端点A．C重合，折痕所在直线交直线AB于点E，如果AB=4，BE=1，则BC的长为______.
22、（4分）当2（x+1）﹣1与3（x﹣2）﹣1的值相等时，此时x的值是_____．
23、（4分）如图，正方形ABCD的对角线相交于点O，点O又是正方形A1B1C1O的一个顶点，而且这两个正方形的边长都为2，无论正方形A1B1C1O绕点O怎样转动，两个正方形重叠部分的面积均为定值__________．
二、解答题（本大题共3个小题，共30分）
24、（8分）某公园有海盗船、摩天轮、碰碰车三个娱乐项目，现要在公园内建一个售票中心，使三个娱乐项目所处位置到售票中心的距离相等，请在图中确定售票中心的位置．
25、（10分）如图所示，△A′B′C′是△ABC经过平移得到的，△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6，y1+4)．
（1）请写出三角形ABC平移的过程；
（2）分别写出点A′，B′，C′ 的坐标．
（3）求△A′B′C′的面积．
26、（12分）亚健康是时下社会热门话题，进行体育锻炼是远离亚健康的一种重要方式，为了解某校八年级学生每天进行体育锻炼的时间情况，随机抽样调查了100名初中学生，根据调查结果得到如图所示的统计图表．
请根据图表信息解答下列问题：
（1）a= ；
（2）补全条形统计图；
（3）小王说：“我每天的锻炼时间是调查所得数据的中位数”，问小王每天进行体育锻炼的时间在什么范围内？
（4）若把每天进行体育锻炼的时间在1小时以上定为锻炼达标，则被抽查学生的达标率是多少？
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
先求出一次函数y=kx+b与x轴和y轴的交点，再利用三角形的面积公式得到关于k的方程，解方程即可求出k的值．
【详解】
解：∵一次函数y=kx+b（k≠0）图象过点（0，3），
∴b=3，
令y=0，则x=-，
∵函数图象与两坐标轴围成的三角形面积为2，
∴×2×|-|=2，
即||=2，
解得：k=±1.5，
则函数的解析式是y＝1.5x＋3或y＝－1.5x＋3.
故选C．
本题考查一次函数图象上点的坐标特征和三角形的面积公式，有一定的综合性，注意点的坐标和线段长度的转化．
2、D
【解析】
直接利用二次根式的性质分别化简得出答案．
【详解】
解：A、，故此选项错误；
B、，故此选项错误；
C、，故此选项错误；
D、，正确．
故选：D．
此题主要考查了二次根式的性质与化简，正确掌握二次根式的性质是解题关键．
3、A
【解析】
根据题意在运动过程中EF∥AC且EF＝AC,所以可得四边形ACFE为平行四边形,因此计算面积即可.
【详解】
根据在运动过程中EF∥AC且EF＝AC
四边形ACFE为平行四边形
过D作DM垂直AC于点M
根据等面积法，在中
可得四边形ACFE为平行四边形的高为

故选A
本题主要考查平行四边形的性质，关键在于计算平行四边形的高.
4、B
【解析】
二次根式的化简：①利用二次根式的基本性质进行化简；②利用积的算术平方根的性质和商的算术平方根的性质进行化简．
【详解】
解：，故A错误；
，故B正确；
，故C错误；
，故D错误．
故选：．
本题考查了二次根式化简，熟练掌握化简二次根式是解题的关键．
5、D
【解析】
矩形的对角线相等且平分，所以，由题中条件可得是等边三角形，可知.
【详解】
解：四边形ABCD是矩形

又

是等边三角形


所以图中长度为3的线段有OA、OB、OC、OD、BC、AD,共6条.
故答案为D
本题考查了等边三角形的判定和性质，有一个角是的等腰三角形是等边三角形，等边三角形的三条边都相等，灵活运用矩形及等边三角形的性质求线段长是解题的关键.
6、B
【解析】
根据等边三角形，可证△AED为等腰三角形，从而可求∠AED，也就可得∠BED的度数．
【详解】
解：∵等边△ABE
∴∠EAB=∠BED=60°，AE=AD
∵四边形ABCD是正方形
∴∠BAD=90°， AB=AD
∴∠EAD=150°，AE=AD
∴∠AED=∠ADE=15°
∴∠BED=60°-15°=45°
故选：B．
此题主要考查了等边三角形的性质．即每个角为60度．
7、B
【解析】
试题解析：小强和小华玩“石头、剪刀、布”游戏，所有可能出现的结果列表如下：
小强
小华 石头 剪刀 布
石头 （石头，石头） （石头，剪刀） （石头，布）
剪刀 （剪刀，石头） （剪刀，剪刀） （剪刀，布）
布 （布，石头） （布，剪刀） （布，布）
∵由表格可知，共有9种等可能情况．其中平局的有3种：（石头，石头）、（剪刀，剪刀）、（布，布）．
∴小明和小颖平局的概率为：．
故选B．
考点：概率公式.
8、C
【解析】
根据最简二次根式的概念：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式进行分析即可.
【详解】
、，故此选项错误；
、，故此选项错误；
、是最简二次根式，故此选项正确；
、，故此选项错误.
故选：.
此题主要考查了最简二次根式，关键是掌握最简二次根式的条件.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
延长BG交CH于点E，根据正方形的性质证明△ABG≌△CDH≌△BCE，可得GE=BE-BG=2、HE=CH-CE=2、∠HEG=90°，由勾股定理可得GH的长．
【详解】
解：如图，延长BG交CH于点E，
∵正方形的边长为5，，
∴AG2+BG2=AB2，
∴∠AGB=90°，
在△ABG和△CDH中，
∴△ABG≌△CDH（SSS），
∴∠1=∠5，∠2=∠6，∠AGB=∠CHD=90°，
∴∠1+∠2=90°，∠5+∠6=90°，
又∵∠2+∠3=90°，∠4+∠5=90°，
∴∠1=∠3=∠5，∠2=∠4=∠6，
在△ABG和△BCE中，
∴△ABG≌△BCE（ASA），
∴BE=AG=4，CE=BG=3，∠BEC=∠AGB=90°，
∴GE=BE-BG=4-3=1，
同理可得HE=1，
在RT△GHE中，
故答案为：
本题主要考查正方形的性质、全等三角形的判定与性质、勾股定理及其逆定理的综合运用，通过证三角形全等得出△GHE为等腰直角三角形是解题的关键．
10、.
【解析】
根据乘方的定义计算即可.
【详解】
（﹣）2＝．
故答案为：．
本题考查了乘方的意义，一般地，n个相同的因数a相乘，即a·a·a·…·a计作an，这种求几个相同因数的积的运算，叫做乘方，乘方的结果叫做幂.在an中，a叫做底数，n叫做指数.
11、7，1
【解析】
由题意知，，
解得x＝7，
这组数据中7，1各出现两次，出现次数最多，
故众数是7，1．
12、或
【解析】
沿着过矩形顶点的一条直线将∠B折叠，可分为两种情况：（1）过点A的直线折叠，（2）过点C的直线折叠，分别画出图形，根据图形分别求出折痕的长．
【详解】
（1）如图1，沿将折叠，使点的对应点落在矩形的边上的点，
由折叠得：是正方形，此时：，
（2）如图2，沿，将折叠，使点的对应点落在矩形的边上的点，
由折叠得：，
在中，，
，
设，则，
在中，由勾股定理得：，解得：，
在中，由勾股定理得：，
折痕长为：或．
考查矩形的性质、轴对称的性质、直角三角形及勾股定理等知识，分类讨论在本题中得以应用，画出相应的图形，依据图形矩形解答．
13、
【解析】
观察分析可得，，，则将此规律用含自然数n(n≥1)的等式表示出来是
【详解】
由分析可知，发现的规律用含自然数n(n≥1)的等式表示出来是
故答案为：
本题主要考查二次根式，找出题中的规律是解题的关键，观察各式，归纳总结得到一般性规律，写出用n表示的等式即可．
三、解答题（本大题共5个小题，共48分）
14、（1）甲；（2）2.1．
【解析】
（1）从平均数与方差上进行分析，根据方差越大，波动越大，数据越不稳定，反之，方差越小，波动越小，数据越稳定即可求出答案；
（2）根据方差的计算公式进行计算即可得．
【详解】
解：（1）从平均数看，甲、乙的平均数一样，都是8分，
从方差看，0.4<3.2，即甲的方差比乙的方差小，甲的成绩比较稳定，因此应该选派甲去参加操作技能大赛；
（2）乙的平均数为：（5+9+7+10+9+8）÷6=8，
方差为：=≈2.1，
答：乙6次测试成绩的方差为2.1．
本题考查了方差的意义，熟练掌握方差的意义以及方差的计算公式是解题的关键．
15、（1）点与之间的距离为：；（2）.
【解析】
（1）根据题意得出∠DFE=30°，则EF=2DE=16，进而利用勾股定理得出DF的长，进而得出答案；
（2）直接利用勾股定理得出DM的长，进而得出MB=FM，求出答案．
【详解】
解：（1）如图，
过点作于点，
在中，，，，
则，
故，
，
∵，
∴，
在中，，
即点与之间的距离为：；
（2）在中，，
∵，
∴，
又∵，
是等腰直角三角形，
∴，
∴．
此题考查勾股定理，平行线的性质，解题关键在于作辅助线
16、 (1)证明见解析；(2)画图见解析.
【解析】
（1）根据平行线的性质和角平分线的定义即可得到结论；
（2）在射线AE上截取AD=AB，根据菱形的判定定理即可得到结论．
【详解】
解：(1)∵AE∥BF，
∴∠EAC=∠ACB，
又∵AC平分∠BAE，
∴∠BAC=∠EAC，
∴∠BAC=∠ACB，
∴BA=BC．
(2)主要作法如下：
本题考查了作图-复杂作图，菱形的判定，正确的作出图形是解题的关键．
17、甲队独做需30天，乙队独做需120天
【解析】
设甲队独做需a天，乙队独做需b天，根据题意可得两个等量关系为：甲工效×工作时间+乙工效×工作时间=1；甲工效×20+乙工效×40=1．列出方程组，再解即可．
【详解】
设甲队独做需a天，乙队独做需b天．
建立方程组 ，
解得 ．
经检验a＝30，b＝120是原方程的解．
答：甲队独做需30天，乙队独做需120天．
本题考查了分式方程（组）的应用．得到工作量1的等量关系是解题的关键．
18、（1）见解析；（2）.
【解析】
（1）通过证明△ODF与△OBE全等即可求得．
（2）由△ADB是等腰直角三角形，得出∠A=45°，因为EF⊥AB，得出∠G=45°，所以△ODG与△DFG都是等腰直角三角形，从而求得DG的长和EF=2，然后平行线分线段成比例定理即可求得．
【详解】
解：（1）四边形是平行四边形，，
，即．
在与中，
，．
（2），
，，
，．
，，，．
，．
，，．
，，．
本题考查全等三角形的判定与性质、平行四边形的性质和等腰直角三角形，解题关键在于证明△ODF与△OBE全等即可
一、填空题（本大题共5个小题，每小题4分，共20分）
19、x≥1
【解析】
根据被开方数大于等于0列式计算即可得解．
【详解】
由题意得，x−1⩾0，
解得x⩾1.
故答案为：x⩾1.
此题考查二次根式有意义的条件，解题关键在于掌握被开方数大于等于0
20、
【解析】
作AE⊥y轴于E，将线段OA绕点O顺时针旋转90°得到OA′，作A′F⊥x轴于F，则△AOE≌△A′OF，可得OF=OE=4，A′F=AE=3，即A′（4，-3），求出线段AA′的中垂线的解析式，利用方程组确定交点坐标即可．
【详解】
解：如图，作AE⊥y轴于E，将线段OA绕点O顺时针旋转90°得到OA′，作A′F⊥x轴于F，则△AOE≌△A′OF，可得OF=OE=5，A′F=AE=4，即A′（5，-4）．
∵反比例函数的图象经过点A（4，5），
所以由勾股定理可知：OA=，
∴k=4×5=20，
∴y=，
∴AA′的中点K（），
∴直线OK的解析式为y=x，
由，
解得或，
∵点P在第一象限，
∴P（），
故答案为（）．
本题考查反比例函数图象上点的坐标特征，一次函数的应用等知识，解题的关键是学会构造全等三角形解决问题，学会构建一次函数，利用方程组确定交点坐标，属于中考填空题中的压轴题．
21、或2
【解析】
分类讨论：当点E在线段AB上，连结CE，根据折叠的性质得到AE=CE=3，然后在Rt△BCE中，利用勾股定理计算BC；当点E在线段AB的延长线上，连结CE，根据折叠的性质得AE=CE=5，在Rt△BCE中，根据勾股定理计算BC．
【详解】
当点E在线段AB上,如图1,连结CE,
∵AB=4，BE=1，
∴AE=3，
∵将矩形ABCD折叠，使得对角线的两个端点A. C重合，
∴AE=CE=3，
在Rt△BCE中,BC=；
当点E在线段AB的延长线上，如图2，连结CE，
∵AB=4，BE=1，
∴AE=5，
∵将矩形ABCD折叠，使得对角线的两个端点A. C重合，
∴AE=CE=5，
在Rt△BCE中,BC=，
∴BC的长为或.
本题考查折叠问题，分情况解答是解题关键.
22、-7.
【解析】
根据负整数指数幂的意义化为分式方程求解即可.
【详解】
∵与的值相等，
∴=，
∴，
两边乘以(x+1)(x-2)，得
2 (x-2)=3(x+1)，
解之得
x=-7.
经检验x=-7是原方程的根.
故答案为-7.
本题考查了负整数指数幂的意义及分式方程的解法，解分式方程的基本思路是把方程的两边都乘以各分母的最简公分母，化为整式方程求解，求出x的值后不要忘记检验.
23、1
【解析】
过点O作OG⊥AB，OH⊥BC，利用AAS证明△EOG≌△FOH，得到两个正方形重合部分的面积是正方形OGBH，由此得到答案.
【详解】
如图，过点O作OG⊥AB，OH⊥BC，则∠OGE=∠OHF=90°，
∵四边形ABCD是正方形，
∴OA=OB=OC，∠AOB=∠BOC=90°，
∴OG=AB=BC=OH=1，∠GOH=90°，
∵四边形A1B1C1O是正方形，
∴∠A1OC1=90°，
∴∠EOG=∠FOH，
∴△EOG≌△FOH，
∵∠ABC=∠OGB=∠OHB=90°，
∴四边形OGBH是矩形，
∵OG=OH，
∴四边形OGBH是正方形，
∴两个正方形重叠部分的面积==1，
故答案为：1.
此题考查正方形的性质，全等三角形的性质，正方形的判定定理，熟记各定理并熟练运用解题是关键.
二、解答题（本大题共3个小题，共30分）
24、见解析
【解析】
由三个娱乐项目所处位置到售票中心的距离相等，可得售票中心是海盗船、摩天轮、碰碰车三个娱乐场组成三角形的三边的垂直平分线的交点．
【详解】
如图，①连接AB，AC，
②分别作线段AB，AC的垂直平分线，两垂直平分线相较于点P，
则P即为售票中心．
此题考查了线段垂直平分线的性质．此题难度不大，注意掌握线段垂直平分线的作法．
25、（1）见解析；（2）A′(2，3) B′（1，0） C′（5，1）；（3）5.5
【解析】
(1)由x1+6-x1=6，y1+4-y1=4得平移规律；
(2)根据(1)中的平移规律即可得到点A′，B′，C′的坐标；
(3)把△A′B′C′补形为一个长方形后，利用面积的和差关系求△A′B′C′的面积.
【详解】
(1) △ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′
(2) A′(2，3) B′（1，0） C′（5，1）;
(3)S△A′B′C′=4×3−×3×1−×3×2−×1×4=12−1.5−3−2=5.5.
26、 (1) 35；（2）答案见解析；（3）1＜t≤1.5；（4）75%．
【解析】
（1）100减去已知数，可得a；（2）根据a=35画出条形图；（3）中位数是第50个和51个数据的平均数；（4）用样本的达标率估计总体的达标情况.
【详解】
解：（1）a=100﹣5﹣20﹣30﹣10=35，
故答案为35；
（2）条形统计图如下：
（3）∵100÷2=50，25＜50＜60，
∴第50个和51个数据都落在C类别1＜t≤1.5的范围内，
即小王每天进行体育锻炼的时间在1＜t≤1.5范围内；
（4）被抽查学生的达标率=×100%=75%．
本题考核知识点：数据的描述，用样本估计总体. 解题关键点：从统计图表获取信息，用样本估计总体.
题号
一
二
三
四
五
总分
得分
5次测试成绩（分）
平均数
方差
甲
8
8
7
8
9
8
0.4
乙
5
9
7
10
9
8
3.2
类别
时间t（小时）
人数
A
t≤0.5
5
B
0.5＜t≤1
20
C
1＜t≤1.5
a
D
1.5＜t≤2
30
E
t＞2
10