浙江省宁波市余姚市六校联考2023-2024学年八年级上学期期中考试数学试卷(含答案)

这是一份浙江省宁波市余姚市六校联考2023-2024学年八年级上学期期中考试数学试卷(含答案)，共6页。试卷主要包含了若，则下列不等式正确的是等内容，欢迎下载使用。

1.在下列交通标志中，是轴对称图形的为（ ）
A. B. C. D.
2.下列长度的三条线段，能组成三角形的是（ ）
A.1，2，3 B.3，5，6 C.4,5,10 D.5，5，12
3.若，则下列不等式正确的是（ ）
A. B.
C. D.
4.能说明命题“对于任意实数，都有”是假命题的反例为（ ）
A. B. C. D.
5.下列各图中，正确画出AC边上的高的是（ ）
A. B. C. D.
6.如图，CD是Rt△ABC的中线，∠ACB=90°，∠ABC=25°，则∠ADC的度数为（ ）
A.60° B.50° C.65° D.55°
第6题图
第6题图
第6题图
第8题图
第6题图
第7题图
7.如图，在△ABC和△DBE中，BE=BC，添加一个条件，不能证明△ABC≌△DBE的是（ ）
A.AB=DB B.∠A=∠D C.AC=DE D.∠ACB=∠DEB
8.如图，AD，CE分别是△ABC的中线和角平分线.若AB=AC，∠CAD=20°，则∠ACE的度
数是（ ）
A.20° B.35° C.40° D.50°
9.如图，AB，BC，CD，DE是四根长度均为5cm的火柴棒，点A，C，E共线.若AC=6，CD ⊥BC，则线段CE的长度是（ ）
A.6cm B.7cm C.cm D.8cm
第10题图
第9题图
10.如图，在Rt△ABC中，∠ACB=90°，分别以AB、AC、BC为边在AB的同侧作正方形
ABEF、ACPQ、BDMC，记四块阴影部分的面积分别为、、、.若已知，则下列结论：①；②；③；④，
其中正确的结论是（ ）
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题（每小题4分，共24分）
11.在△ABC中，∠A=45°，∠B=75°，则∠C的度数为 .
12.“与5的差大于的4倍”用不等式表示为 .
13.若等腰三角形的一个内角为50°，则其顶角为 .
14.如图，在△ABC中，CD是AB边上的高，BE平分∠ABC交CD于点E，BC=5.若△BCE
的面积为5，则ED的长为 .
15.如图，在长方形ABCD中，AB=8，BC=10，在边CD上取一点E，将△ADE折叠使点D
恰好落在BC边上的点F，则CE的长为 .
16.如图，在边长为2的等边三角形中，点D，E分别是BC，AB的中点，点P是AD上一动点，则△PBE的周长最小值为 .
第16题图
第15题图
第14题图
三、解答题（共66分）
17.（6分）已知：如图，点E，F在BC边上，BE=CF，∠AFE=∠DEC，∠B=∠C，AF与DE交于点O.求证：AB=DC.
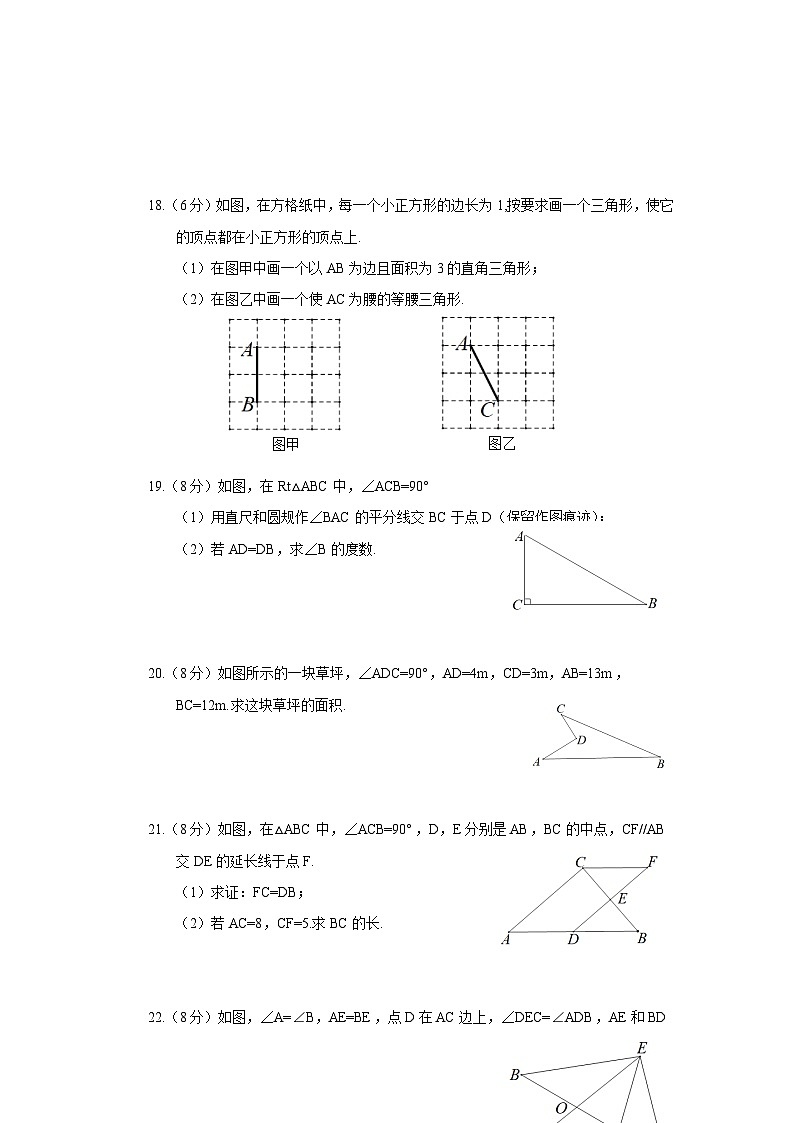
18.（6分）如图，在方格纸中，每一个小正方形的边长为1,按要求画一个三角形，使它的顶点都在小正方形的顶点上.
（1）在图甲中画一个以AB为边且面积为3的直角三角形；
（2）在图乙中画一个使AC为腰的等腰三角形.
图甲
图乙
19.（8分）如图，在Rt△ABC中，∠ACB=90°
（1）用直尺和圆规作∠BAC的平分线交BC于点D（保留作图痕迹）；
（2）若AD=DB，求∠B的度数.
20.（8分）如图所示的一块草坪，∠ADC=90°，AD=4m，CD=3m，AB=13m，BC=12m.求这块草坪的面积.
21.（8分）如图，在△ABC中，∠ACB=90°，D，E分别是AB，BC的中点，CF//AB交DE的延长线于点F.
（1）求证：FC=DB；
（2）若AC=8，CF=5.求BC的长.

22.（8分）如图，∠A=∠B，AE=BE，点D在AC边上，∠DEC=∠ADB，AE和BD相交于点O.
（1）求证：△AEC≌△BED；
（2）若∠DEC=38°，求∠BDE度数.
23.（10分）如图，在Rt△ABC中，∠ACB=90°，AC=CB，D在BC边上，P，Q是射线AD上两点，且CP=CQ，∠PCQ=90°.
（1）求证：AP=BQ；
（2）若CP=1，BP=.
①求AP的长；
②求△ABC的面积.
24.（12分）定义：若以三条线段，，为边能构成一个直角三角形，则称线段，，是勾股线段组.
（1）如图①，已知点M，N是线段AB上的点，线段AM，MN，NB是勾股线段组.若AB=12，AM=3，求MN的长；
（2）如图②，△ABC中，∠A=17°，∠B=28°，边AC，BC的垂直平分线分别交AB于点M，N，求证：线段AM，MN，NB是勾股线段组；
（3）如图③，在等边△ABC，P为△ABC内一点，线段AP，BP，CP构成勾股线段组，CP为此线段组的最长线段，求∠APB的度数.
图②
图①
图③
数学学科参考答案
选择题（每题3分，共30分）
D 2.B 3.A 4.C 5.D 6.B 7.C 8.B 9.D 10.A
填空题（每题4分，共24分）
60° 12. 13. 50°或80° 14. 2 15. 3 16. 1+
解答题
证明：∵BE=CF，
∴BF=CE，（2分）
又∵∠AFB=∠DEC，∠B=∠C，
∴△ABF≌△DCE（ASA）（4分）
∴AB=DC（6分）
（答案不唯一）
（2）
（3分） （6）
（1）作图，略.（4分）
解：∵AD=BD，
∴∠DAB=∠B，
又∵∠CAD=∠DAB，
∴∠CAD=∠DAB=∠B，
∴3∠B=90°，
∴∠B=30°（8分）
解：连结AC，
∵∠ADC=90°，AD=4，CD=3
∴AC=5 （3分）
又∵AB=13，BC=12，
∴AC2+BC2=AB2
∴∠ACB=90°，（6分）
∴S=30-6=24 （8分）
解：（1）∵CF//AB，∴∠F=∠FDB，∠FCB=∠B，
又∵E是BC中点，∴CE=BE，
∴△CFE≌△BDE（AAS）
∴FC=DB.（4分）
（2）由（1）得，BD=CF=5，
∵D是AB中点，∴AB=10，
∵AC=8，∠ACB=90°，
∴BC=6.（8分）
证明：（1）∵∠A=∠B，∠BOE=∠DOA
∴∠BEA=∠BDA，
∵∠BDA=∠DEC，
∴∠BEA=∠CED，
∴∠BED=∠AEC，
又∵BE=AE，
∴△AEC≌△BED（ASA）（4分）
（2）∵DE=CE，∠DEC=38°，
∴∠C=71°，
∴∠BDE=∠C=71°（8分）
23.证明：（1）∵∠QCP=∠BCA=90°，
∴∠QCB=∠PCA，
又∵CQ=CP，CB=CA，
∴△QCB≌△PCA（SAS）
∴AP=BQ（3分）
（2）①∵CP=1，∴CQ=1，
∵∠QCP=90°，∴QP=，∠CQP=∠CPQ=45°，
∴∠CPA=∠CQB=135°，
∴∠BPQ=90°，∴AP=2（6分）
②△ABC的面积为△BQA与△QCP面积之和
S= （10分）
24.（1）∵AB=12，AM=3，
∴MB=9，
设MN=x
①若MN为直角边，
32+x2=（9-x）2
X=4
②若MN为斜边
32+（9-x）2=x2
X=5
∴MN=4或5 （4分）
（2）连结CM，CN，
由题意得，AM=CM，BN=CN，
∴∠A=∠ACM=17°，∠B=∠NCB=28°，
∴∠A+∠ACM+∠B+∠BCN=90°，
∴∠MCN=90°，
∴CM，CN，MN为勾股线段组，
∴AM，MN，NB为勾股线段组 （8分）
将△ABP绕点A逆时针旋转60°得到△ACH，
∵AP=AH，∠PAH=60°，
∴∠AHP=60°，
又∵AP，BP，CP为勾股线段组，BP=CH，PH=AP，
∴PH2+CH2=PC2，
∴∠PHC=90° ∴∠APB=∠AHC=150°（12分）