2023-2024学年山东省威海市环翠区八年级（上）期末数学试卷（五四学制）（含答案）

这是一份2023-2024学年山东省威海市环翠区八年级（上）期末数学试卷（五四学制）（含答案），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。
1.下列图形中是中心对称的是( )
A. B. C. D.
2.下列由左边到右边的变形，是因式分解的是( )
A. m(a+b)=am+bmB. 4x2−2x=x(4x−2)
C. y2−1−3y=(y+1)(y−1)−3yD. m2−16=(m+4)(m−4)
3.已知一个样本数据为2，3，4，5，6，则这组数据的方差和标准差分别是( )
A. 2， 2B. 3， 3C. 2，2D. 3，3
4.关于平行四边形的性质，下列描述错误的是( )
A. 平行四边形既是轴对称图形又是中心对称图形
B. 平行四边形的对角相等
C. 平行四边形的对角线互相平分
D. 平行四边形的对边平行且相等
5.经过28分钟，时针旋转了( )度．
A. 7B. 14C. 21D. 28
6.将点A先向下平移5个单位，再向右平移3个单位得到点A′坐标为(4,−2)，则点A坐标为( )
A. (9,3)B. (7,−7)C. (−1,1)D. (1,3)
7.下列分式是最简分式的是( )
A. 2a+64aB. 3a−3ba2−b2C. m−n−m+nD. m−5m+n
8.若正多边形的一个外角为30度，则多边形的内角和为( )度．
A. 1620B. 1800C. 1980D. 2160
9.为了解某公司员工的年收入情况，小丽随机调查了该公司10名员工，其年收入(单位：万元)为4，4，5，5，5，6，6，6，8，20.下列说法正确的是( )
A. 平均数可以反映该公司员工年工资水平B. 众数是5
C. 中位数是5.5D. 平均数是6.6
10.如图，点F，G，H分别是AD，BD，BC边的中点，且AB=CD，∠ABD=30°，∠BDC=80°，则∠GHF=( )
A. 25°
B. 30°
C. 35°
D. 40°
二、填空题：本题共6小题，每小题3分，共18分。
11.如图，∠A+∠B+∠D+∠E+∠G+∠I= ______．
12.化简(a+b)÷(a−b)⋅1a−b= ______．
13.下列说法：①成中心对称的两个图形全等；②多项式15a3b5c4−20a4b3c2+25a2b2c3各项的公因式是a2b2c2；③标准差不可能是0；④因为x2x=x，而x取任意实数都有意义，所以使分式x2x有意义的条件是x为任意实数.以上说法中错误的是______.(请填序号)
14.已知264−1能被在10到20之间的两个整数整除，则这两个整数为______．
15.某校规定学生的劳动教育成绩由三部分组成：理论知识占20%，劳动技能占50%，劳动成果占30%.A同学这三部分成绩分别为80分，98分，98分，则A同学最终劳动成绩为______分.
16.已知m+1m=3，则5m24m4−m2+4= ______．
三、解答题：本题共7小题，共56分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
把下列各式分解因式．
(1)3x2−2x+13；
(2)(x2+1)2−4x2；
(3)x4−4(实数范围内)；
(4)x2−9−6(3−x)．
18.(本小题8分)
先化简，再求值：(x+1+1x−1)÷x3x2−2x+1，其中x是满足条件x≤2的合适的非负整数．
19.(本小题8分)
已知关于x的分式方程3x−1=nx3−3x+1．
(1)若这个方程无解，求n的值；
(2)若这个方程的解是非负数，求n的值．
20.(本小题8分)
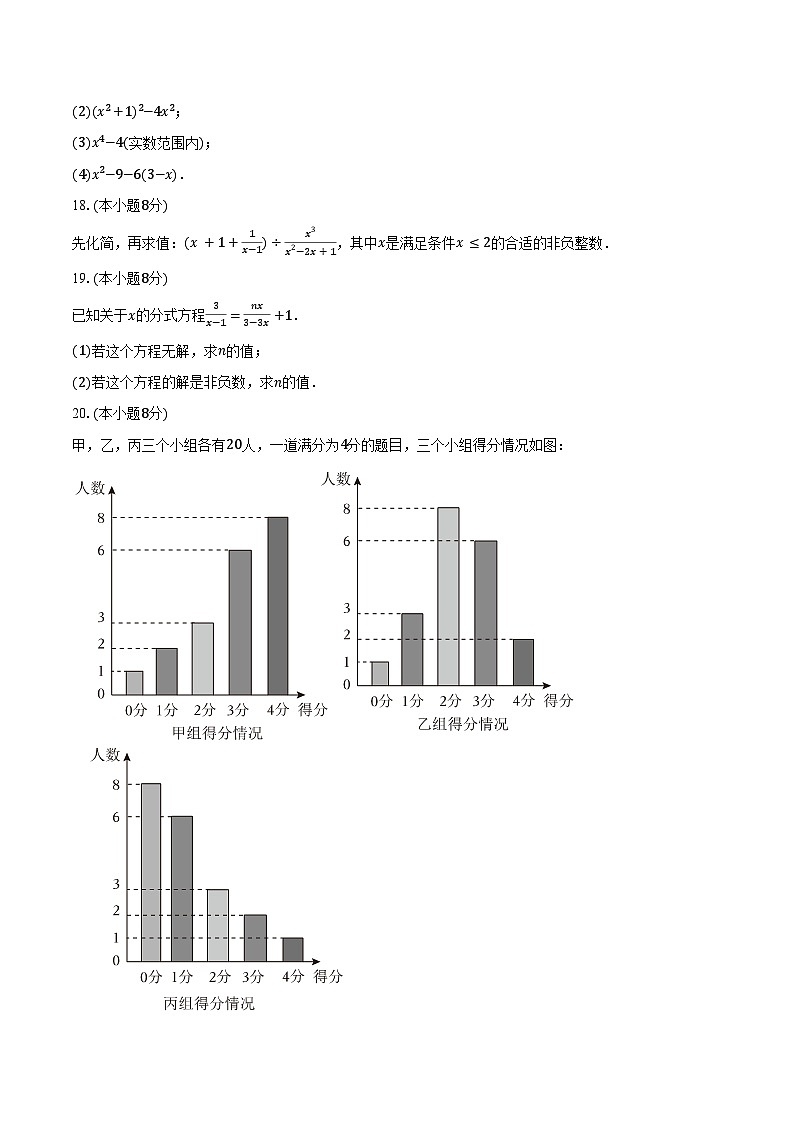
甲，乙，丙三个小组各有20人，一道满分为4分的题目，三个小组得分情况如图：

(1)请计算甲组的平均数和方差；
(2)乙组和丙组平均数和方差如下表：
得分情况最稳定的小组是______组；
(3)对比这三组数据，“柱子的高度”都是1，2，3，6，8，但是它们的排序不同，导致了平均数和方差各不相同，你能否谈谈你的想法，如何排序可以使平均数最大？如何排序可以使方差最小？
21.(本小题8分)
如图，在▱ABCD中，AE=14AD，CF=14BC，求证：EG=FH．
22.(本小题8分)
A，B两公司全体员工踊跃地为甘肃地震捐款，A公司共捐款20万元，B公司共捐款30万元.下面是A，B两公司员工的一段对话：
A公司员工：我们公司员工总数比你们少50人；
B公司员工：你们公司员工人均捐款数是我们公司人均捐款数的45．
请问：A，B两公司各多少员工？
23.(本小题8分)
如图1，已知点D是等边△ABC内一点，且BD=3，AD=4，CD=5．
(1)求∠ADB的度数；
以下是甲，乙，丙三位同学的谈话：
甲：我认为这道题的解决思路是借助旋转，我选择将△BCD绕点B顺时针旋转60°或绕A逆时针旋转60°；
乙：我也赞成旋转，不过我是将△ABD进行旋转；
丙：我是将△ACD进行旋转．
请你借助甲，乙，丙三位同学的提示，选择适当的方法求∠ADB的度数；
(2)若改成BD=6，AD=8，CD=10，∠ADB的度数= ______°，点A到BD的距离为______；
类比迁移：
(3)如图2，已知，∠ABC=90°，AB=BC，BE=1，CE= 3，AE= 5，求∠BEC的度数．
参考答案
1.C
2.D
3.A
4.A
5.B
6.D
7.D
8.B
9.C
10.A
11.360°
12.a+b(a−b)2
13.②③④
14.17和15
15.94.4
16.527
17.解：(1)3x2−2x+13
=3(x2−23x+19)
=3(x−13)2；
(2)(x2+1)2−4x2
=(x2+1+2x)(x2+1−2x)
=(x+1)2(x−1)2；
(3)x4−4
=(x2+2)(x2−2)
=(x2+2)(x+ 2)(x− 2)；
(4)x2−9−6(3−x)
=x2−9−18+6x
=x2+6x−27
=(x+9)(x−3)．
18.解：原式=(x2−1x−1+1x−1)⋅(x−1)2x3
=x2x−1⋅(x−1)2x3
=x−1x，
∵x−1≠0且x≠0，
∴x≠1且x≠0，
则满足条件x≤2的合适的非负整数为x=2，
∴原式=2−12=12．
19.解：(1)3x−1=nx3−3x+1，
两边都乘以3−3x，得
−9=nx+3−3x，
∴(n−3)x=−12，
当n−3=0时，分式方程无解，此时n=3．
当x=1时，分式方程无解，此时n−3=−12即n=−9．
综上可知，若这个方程无解，n的值为3或−9；
(2)∵(n−3)x=−12，
∴x=−12n−3，
由题意，得
−12n−3≥0且−12n−3≠1，
解得n<3且n≠−9．
20.(1)根据题意得：
甲组的平均数是：x−=120×(0×1+1×2+2×3+3×6+4×8)=2.9，
甲组的方差是：S2=120×[(0−2.9)2×1+(1−2.9)2×2+(2−2.9)2×3+(3−2.9)2×6+(4−2.9)2×8]=1.39．
(2)乙．
(3)∵得高分的人数越多，平均数越大，
∴甲组的排序平均数最大；
∵离平均数数值接近的人数越多，方差越小，
∴乙组的排序方差最小．
21.证明：在▱ABCD中，AE=14AD，CF=14BC，AD=BC，
∴AE=CF且AE//CF，DE=BF，DE//BF，
∴四边形AECF是平行四边形，四边形DEBF是平行四边形，
∴GF//EH，GE//FH，
∴四边形EGFH是平行四边形，
∴EG=FH．
22.解：设A公司有x人，则B公司有(x+50)人，
依题意，得：200000x=300000x+50×45，
解得：x=250，
经检验，x=250是原方程的解，且符合题意，
∴x+50=300．
答：A公司有250人，B公司有300人．
23.(1)如图1，将△ABD绕点A逆时针旋转60°，得到△CD′A，
∴D′A=AD=4，BD=CD′=3，∠DAD′=60°，
∴△ADD′是等边三角形，
∴DD′=AD=4，∠AD′D=60°，
∵DD′2+CD′2=42+32=52=CD2，
∴∠DD′C=90°，
∴∠ADB=∠AD′C=60°+90°=150°；
(2)150，4；
(3)如图2，把△CBE绕着点B顺时针旋转90°，得到△BAE′，连接EE′，
∴∠EBE′是直角，BE=BE′=1，AE′=CE= 3，∠AE′B=∠CEB，
∴EE′2=12+12=2，∠BEE′=∠BE′E=45°，
∵EE′2=2，AE′2=3，EA2=5，
∴EA2=E′A2+EE′2，
∴△EE′A是直角三角形，
∴∠EE′A=90°，
∴∠BEC=∠AE′B=135°．
乙组
丙组
平均数
2.25
1.1
方差
0.9875
1.39