2024-2025学年河南省信阳市光山县慧泉中学九年级（上）开学数学试卷（含详解）

这是一份2024-2025学年河南省信阳市光山县慧泉中学九年级（上）开学数学试卷（含详解），共14页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。
1.下列方程中是关于x的一元二次方程的是( )
A. 3x2−2xy−5y2=0B. (x−1)(x+2)=1
C. ax2+bx+c=0D. x2+1x2=0
2.方程4x2−12x=3的根的情况为( )
A. 有两个不相等的实数根B. 有两个相等的实数根
C. 无实数根D. 无法确定
3.若a是方程x2+3x−1=0的一个根，则a2+3a+2022=( )
A. −2021B. 2023C. 2021D. 2022
4.抛物线y=3(x−1)2+1的顶点坐标是( )
A. (1,1)B. (−1,1)C. (−1,−1)D. (1,−1)
5.已知抛物线y=ax2−4ax+ℎ(a≠0)与x轴交于A(x1,0)，B(3,0)两点，则线段AB的长度为( )
A. 1B. 2C. 3D. 4
6.对于二次函数y=2(x+1)(x−3)，下列说法正确的是( )
A. 图象的开口向下B. 当x>1时，y随x的增大而减小
C. 当x<1时，y随x的增大而减小D. 图象的对称轴是直线x=−1
7.电影《长津湖》讲述了一段波澜壮阔的历史，一上映就获得全国人民的追捧.已知第一天票房约为2亿元，前三天票房累计约10亿元.若每天票房的增长率都为x，依题意可列方程为( )
A. 2(1+x)=10B. 2(1+x)2=10
C. 2+2(1+x)2=10D. 2+2(1+x)+2(1+x)2=10
8.已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
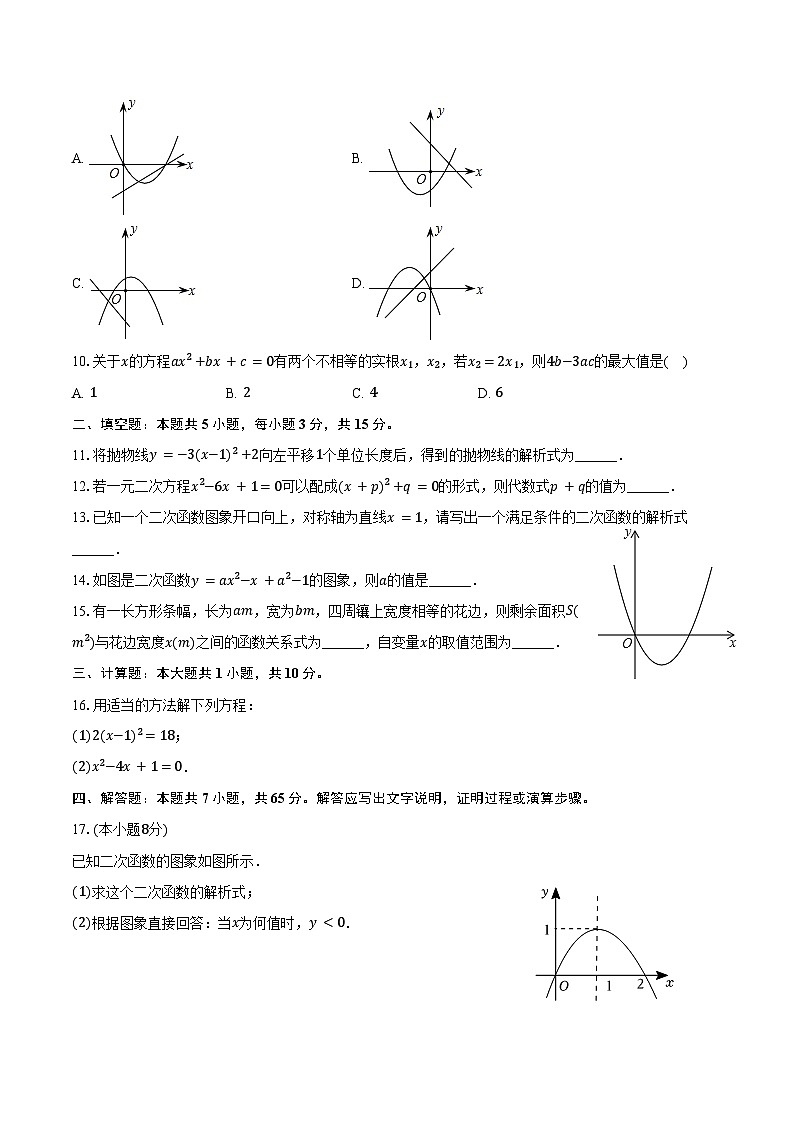
点A(x1,y1)、B(x2,y2)在函数的图象上，则当1A. y1>y2B. y19.在同一平面直角坐标系中，一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )
A. B.
C. D.
10.关于x的方程ax2+bx+c=0有两个不相等的实根x1，x2，若x2=2x1，则4b−3ac的最大值是( )
A. 1B. 2C. 4D. 6
二、填空题：本题共5小题，每小题3分，共15分。
11.将抛物线y=−3(x−1)2+2向左平移1个单位长度后，得到的抛物线的解析式为______．
12.若一元二次方程x2−6x+1=0可以配成(x+p)2+q=0的形式，则代数式p+q的值为______．
13.已知一个二次函数图象开口向上，对称轴为直线x=1，请写出一个满足条件的二次函数的解析式______．
14.如图是二次函数y=ax2−x+a2−1的图象，则a的值是______．
15.有一长方形条幅，长为am，宽为bm，四周镶上宽度相等的花边，则剩余面积S(m2)与花边宽度x(m)之间的函数关系式为______，自变量x的取值范围为______．
三、计算题：本大题共1小题，共10分。
16.用适当的方法解下列方程：
(1)2(x−1)2=18；
(2)x2−4x+1=0．
四、解答题：本题共7小题，共65分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
已知二次函数的图象如图所示．
(1)求这个二次函数的解析式；
(2)根据图象直接回答：当x为何值时，y<0．
18.(本小题9分)
已知关于x的一元二次方程：2x2+(m−2)x−m=0．
(1)求证：不论m为何实数，方程总有实数根；
(2)当m=−7时，此方程的两个根分别是菱形ABCD两条对角线长，求菱形ABCD的面积．
19.(本小题9分)
如图，已知抛物线y=x2+bx+c经过A(−1,0)，B(3,0)两点．
(1)求抛物线的解析式和顶点坐标；
(2)点P为抛物线上一点，若S△PAB=10，求出此时点P的坐标．
20.(本小题9分)
如图，在△ABC中，∠C=90°，AC=6cm，BC=8cm，点P从点A出发沿边AC向点C以1cm/s的速度移动，点Q从C点出发沿CB边向点B以2cm/s的速度移动．
(1)如果P、Q同时出发，几秒钟后，可使△PCQ的面积为8平方厘米？
(2)点P、Q在移动过程中，是否存在某点时刻，使得△PCQ的面积等于△ABC的面积的一半？若存在，求出运动的时间；若不存在，说明理由．
21.(本小题10分)
某商场要经营一种新上市的文具，进价为20元/件，试营销阶段发现：当销售单价25元/件时，每天的销售量是250件，销售单价每上涨1元，每天的销售量就减少10件．
(1)写出商场销售这种文具，每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式；
(2)求销售单价为多少元时，该文具每天的销售利润最大；
(3)商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每件文具的利润不低于25元且不高于29元．
请比较哪种方案的最大利润更高，并说明理由．
22.(本小题10分)
如图，一小球M从斜坡OA上的O点处抛出，球的抛出路线是抛物线的一部分，建立如图所示的平面直角坐标系，斜坡可以用一次函数y=12x刻画．若小球到达的最高的点坐标为(4,8)，解答下列问题：
(1)求抛物线的表达式；
(2)在斜坡OA上的B点有一棵树，B点的横坐标为2，树高为4，小球M能否飞过这棵树？通过计算说明理由；
(3)求小球M在飞行的过程中离斜坡OA的最大高度．
23.(本小题10分)
如图，在6×8的网格纸中，每个小正方形的边长都为1，动点P，Q分别从点F，A出发向右移动，点P的运动速度为每秒2个单位，点Q的运动速度为每秒1个单位，当点P运动到点E时，两个点都停止运动．
(1)请你在图1中，画出2秒时的线段PQ；
(2)如图2，在动点P，Q运动的过程中，当运动时间t(s)为何值时，9PQ2=4BF2？
(3)在动点P，Q运动的过程中，△PQB能否成为等腰三角形？若能，请求出相应的时间t；若不能，请说明理由．
答案解析
1.B
【解析】解：A、是二元二次方程，故本选项错误；
B、整理为x2+x−3=0，是关于x的一元二次方程，故本选项正确；
C、a=0时，是关于x的一元一次方程，故本选项错误；
D、分母上有未知数，不是整式方程，故本选项错误．
故选：B．
根据一元二次方程必须满足两个条件：(1)未知数的最高次数是2；(2)二次项系数不为0，对各选项分析判断后利用排除法求解．
本题利用了一元二次方程的概念．只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程，一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．
2.A
【解析】解：原方程可化为4x2−12x−3=0，
∵Δ=(−12)2−4×4×(−3)=144+48=192>0，
∴方程有两个不相等的实数根．
故选：A．
求出一元二次方程根的判别式的值，进而可得出结论．
本题考查的是一元二次方程根的判别式，一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系：
①当Δ>0时，方程有两个不相等的两个实数根；
②当Δ=0时，方程有两个相等的两个实数根；
③当Δ<0时，方程无实数根．
3.B
【解析】解：∵a是方程x2+3x−1=0的一个根，
∴a2+3a−1=0，
∴a2+3a=1，
∴a2+3a+2022=1+2022=2023．
故选B．
4.A
【解析】解：由y=3(x−1)2+1，根据顶点式的坐标特点可知，顶点坐标为(1,1)，
故选：A．
已知抛物线的顶点式，可直接写出顶点坐标．
考查将解析式化为顶点式y=a(x−ℎ)2+k，顶点坐标是(ℎ,k)，对称轴是x=ℎ．
5.B
【解析】解：∵y=ax2−4ax+ℎ(a≠0)的对称轴是：x=−−4a2a=2，
∴A(x1,0)与B(3,0)关于直线x=2对称，
∴A点的坐标是：(1,0)，
∴线段AB的长度=3−1=2；
故选：B．
先求出抛物线的对称轴，再根据A(x1,0)与B(3,0)关于直线x=2对称，求出A点的坐标，即可得出答案．
此题考查了抛物线与x轴的交点；关键是根据抛物线的对称轴求出点A的坐标．
6.C
【解析】解：二次函数y=2(x+1)(x−3)可化为y=2(x−1)2−8的形式，
A、∵此二次函数中a=2>0，∴抛物线开口向上，故本选项错误；
B、∵由二次函数的解析式可知，此抛物线开口向上，对称轴为x=1，∴当x>1时，y随x的增大而增大，故本选项错误；
C、∵由二次函数的解析式可知，此抛物线开口向上，对称轴为x=1，∴当x<1时，y随x的增大而减小，故本选项正确；
D、由二次函数的解析式可知抛物线对称轴为x=1，故本选项错误．
故选：C．
先把二次函数化为顶点式的形式，再根据二次函数的性质进行解答．
本题考查的是二次函数的性质，根据题意把二次函数化为顶点式的形式是解答此题的关键．
7.D
【解析】解：依题意，得：2+2(1+x)+2(1+x)2=10．
故选：D．
根据第一天的票房收入及前三天的票房收入，即可得出关于x的一元二次方程，此题得解．
本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
8.B
【解析】解：∵当1∴y1故选B．
由表格可知，当1本题考查了二次函数图象上点的坐标特点．关键是由表格判断自变量取值范围内，函数值的大小．
9.A
【解析】解：A、由抛物线可知，a>0，x=−b2a>0，得b<0，由直线可知，a>0，b<0，正确；
B、由抛物线可知，a>0，由直线可知，a<0，错误；
C、由抛物线可知，a<0，x=−b2a>0，得b>0，由直线可知，a<0，b<0，错误；
D、由抛物线可知，a<0，由直线可知，a>0，错误．
故选：A．
本题可先由一次函数y=ax+b图象得到字母系数的正负，再与二次函数y=ax2+bx+c的图象相比较看是否一致．
本题考查抛物线和直线的性质，用假设法来搞定这种数形结合题是一种很好的方法．
10.D
【解析】解：∵关于x的方程ax2+bx+c=0有两个不相等的实根x1、x2，
∴x1+x2=−ba，x1x2=ca，
∵x2=2x1，
∴3x1=−ba，即x1=−b3a，
∴x2=−2b3a，
∴ca=2b29a2，
∴ac=29b2，
∴4b−3ac=4b−3×29b2=4b−23b2=−23(b−3)2+6，
∵−23<0，
∴4b−3ac的最大值是6，
故选：D．
根据根与系数的关系得出x1+x2=−ba，x1x2=ca，由x2=2x1得出3x1=−ba，即x1=−b3a，可解出x2，由两根之积可得ac=29b2，代入代数式即可得到4b−3ac=−23(b−3)2+6，从而求得4b−3ac的最大值是6．
此题主要考查了根与系数的关系，由x1+x2=−ba，x2=2x1，得出x1=−b3a，代入方程得到ac=29b2是解决问题的关键．
11.y=−3x2+2
【解析】解：将抛物线y=−3(x−1)2+2向左平移1个单位长度后，得到的抛物线的解析式为y=−3(x−1+1)2+2，即y=−3x2+2．
故答案为：y=−3x2+2．
直接根据“上加下减，左加右减”的原则进行解答．
本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
12.−11
【解析】解：∵x2−6x+1=0，
∴x2−6x=−1，
∴x2−6x+9=−1+9，即(x−3)2=8，
∴p=−3，q=−8，
则p+q=−3−8=−11，
故答案为：−11．
根据配方法解一元二次方程的步骤得出p、q的值，据此可得答案．
本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
13.y=x2−2x+1(答案不唯一)
【解析】解：设所求二次函数的解析式为y=ax2+bx+c(a≠0)．
∵图象的开口向上，
∴a>0，可取a=1，
∵对称轴是直线x=1，
∴−b2a=1，得b=−2a=−2，
∵c可取任意数，
∴函数解析式可以为：y=x2−2x+1(答案不唯一)．
故答案为：y=x2−2x+1(答案不唯一)．
由题意可知：写出的函数解析式满足a>0，−b2a=1，由此举例得出答案即可．
本题考查了二次函数的性质，用到的知识点：二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=−b2a；当a>0时，抛物线开口向上，当a<0时，抛物线开口向下；二次函数与y轴交于点(0,c)．
14.1
【解析】解：∵图象过原点，
∴a2−1=0，
∴a=±1，
∵抛物线的开口方向向上，
∴a>0，
∴a=1．
把原点坐标代入二次函数y=ax2−x+a2−1，即可求出a的值．
考查抛物线图象的开口方向、图象过原点与二次函数系数的关系．
15.s=(a−2x)(b−2x) 0【解析】解：剩余长方形的长为(a−2x)，宽为(b−2x)，
则剩余面积S(m2)与花边宽度x(m)之间的函数关系式为：s=(a−2x)(b−2x)．
∵x>0，2x∴自变量x的取值范围为0故答案为：s=(a−2x)(b−2x)；0因为四周镶上宽度相等的花边，所以剩余长方形的长为(a−2x)，宽为(b−2x)，利用长方形的面积公式：长×宽，可表示出函数关系式；2x应该小于宽b，可求得x的上限，下限为x>0，所以可求出自变量x的取值范围．
主要考查了二次函数的实际运用．用含x的代数式表示出长和宽，再根据长方形的面积公式即可表示出二次函数的解析式．
16.解：(1)2(x−1)2=18，
(x−1)2=9，
开方得：x−1=±3，
解得：x1=4，x2=−2；
(2)x2−4x+1=0，
移项，得x2−4x=−1，
配方，得x2−4x+4=−1+4，
(x−2)2=3，
开方，得x−2=± 3，
解得：x1=2+ 3，x2=2− 3．
【解析】(1)方程两边都除以2，再开方，最后求出方程的解即可；
(2)移项后配方，开方，再求出方程的解即可．
本题考查了解一元二次方程，能选择适当的方法解方程是解此题的关键，注意：解一元二次方程的方法有直接开平方法，公式法，配方法，因式分解法等．
17.解：(1)设解析式为y=ax2+bx+c．
∵图象过点(1,1)，(2,0)，(0,0)，
∴a+b+c=14a+2b+c=0c=0，
解得a=−1b=2c=0，
∴二次函数的解析式为y=−x2+2x；
(2)根据图象知，当x<0或x>2时，y<0．
【解析】
(1)根据图象特点，可设解析式为交点式或一般式求解；
(2)利用图象在x轴下方的图象y小于0得解．
此题考查了运用待定系数法求函数解析式、运用图象得出函数与不等式的关系等知识点．利用数形结合得出是解题关键．
18.(1)证明：∵Δ=(m−2)2−4×2(−m)
=m2−4m+4+8m
=(m+2)2≥0，
∴不论m为何实数，方程总有实数根；
(2)解：当m=−7时，方程为2x2−9x+7=0，
设方程的两根分别为x1，x2，
由根与系数关系得x1x2=72，
S菱形ABCD=12x1x2=12×72=74．
所以菱形ABCD的面积是74．
【解析】(1)先计算判别式的值，再利用配方法得到Δ=(m+2)2，则△≥0，然后根据判别式的意义得到结论；
(2)当m=−7时，方程为2x2−9x+7=0，设方程的两根分别为x1，x2，则根据根与系数关系可得x1x2=72，然后根据菱形的面积公式求解．
本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0(a≠0)的两根，则x1+x2=−ba，x1x2=ca.也考查了根的判别式和菱形的性质．
19.解：(1)把A(−1,0)，B(3,0)代入y=x2+bx+c，
得{1−b+c=09+3b+c=0，解得{b=−2c=−3,
∴抛物线的解析式为y=x2−2x−3=(x−1)2−4，
∴抛物线的顶点坐标为(1,−4)；
(2)∵A(−1,0)，B(3,0)，
∴AB=3−(−1)=4，
设点P的坐标为(t,t2−2t−3)，
∵S△PAB=10，
∴12×4×|t2−2t−3|=10，
∴|t2−2t−3|=5，
当t2−2t−3=5时，解得t1=−2，t2=4，此时点P的坐标为(−2,5)或(4,5)；
当t2−2t−3=−5时，方程没有实数解．
综上所述，此时点P的坐标为(−2,5)或(4,5)．
【解析】(1)把A，B两点的坐标分别代入y=x2+bx+c，得{1−b+c=09+3b+c=0，然后解方程组求出b，c的值，即可得出抛物线的解析式，配成顶点式即可得出抛物线的顶点坐标；
(2)设点P的坐标为(t,t2−2t−3)，利用三角形面积公式得到12×4×|t2−2t−3|=10，然后分别解方程t2−2t−3=5和t2−2t−3=−5，求出t的值，即可得到点P的坐标．
20.解：(1)设x秒钟后，可使△PCQ的面积为8平方厘米，由题意得：
12(6−x)⋅2x=8，
x=2或x=4，
当2秒或4秒时，面积可为8平方厘米；
(2)不存在．
理由：设y秒时，△PCQ的面积等于△ABC的面积的一半，由题意得：
12(6−y)⋅2y=12×12×6×8
y2−6y+12=0．
△=36−4×12<0．
方程无解，所以不存在．
【解析】(1)设x秒钟后，可使△PCQ的面积为8平方厘米，用x表示出△PCQ的边长，根据面积是8可列方程求解．
(2)假设y秒时，△PCQ的面积等于△ABC的面积的一半，列出方程看看解的情况，可知是否有解．
本题考查一元二次方程的应用，三角形的面积公式的求法，和一元二次方程的解的情况．
21.解：(1)由题意得，销售量=250−10(x−25)=−10x+500，
则w=(x−20)(−10x+500)
=−10x2+700x−10000；
(2)w=−10x2+700x−10000=−10(x−35)2+2250．
∵−10<0，
∴函数图象开口向下，w有最大值，
当x=35时，w最大=2250，
故当单价为35元时，该文具每天的利润最大；
(3)A方案利润高．理由如下：
A方案中：20故当x=30时，w有最大值，
此时wA=2000；
B方案中：
故x的取值范围为：45≤x≤49，
∵函数w=−10(x−35)2+2250，对称轴为直线x=35，
∴当x=45时，w有最大值，
此时wB=1250，
∵wA>wB，
∴A方案利润更高．
【解析】本题考查了二次函数的应用，难度一般．
(1)根据利润=(销售单价−进价)×销售量，列出函数关系式即可；
(2)根据(1)式列出的函数关系式，运用配方法求最大值；
(3)分别求出方案A、B中x的取值范围，然后分别求出A、B方案的最大利润，然后进行比较．
22.解：(1)∵小球到达的最高的点坐标为(4,8)，
∴设抛物线的表达式为y=a(x−4)2+8，
把(0,0)代入得，0=a(0−4)2+8，
解得：a=−12，
∴抛物线的表达式为y=−12(x−4)2+8；
(2)当x=2时，y1=12x=1，y2=−12(x−4)2+8=6，
∵6−1>4，
∴小球M能飞过这棵树；
(3)小球M在飞行的过程中离斜坡OA的高度ℎ=−12(x−4)2+8−12x=−12(x−72)2+498，
∴小球M在飞行的过程中离斜坡OA的最大高度为498．
【解析】(1)设抛物线的表达式为y=a(x−4)2+8，把(0,0)代入即可得到答案；
(2)把x=2分别代入y=−12(x−4)2+8和y=12x，即可得到答案；
(3)根据二次函数的性质即可得到结论．
本题考查了二次函数的应用，其中涉及到两函数图象交点的求解方法，二次函数顶点坐标的求解方法，待定系数法求一次函数的解析式，难度适中．利用数形结合与方程思想是解题的关键．
23.解：(1)如图1中，线段PQ即为所求作．
(2)由题意，9(t2+62)=4(62+82)，
解得t=2 193．
(3)如图2中，作QS⊥FE于S，则PS=2t−t=t，
在Rt△PSQ中，QP2=QS2+PS2，即QP2=62+t2，
①当PB=PQ时，QP2=62+t2，PB2=62+(8−2t)2；
解得，t=83或8(舍去)；
②当QB=QP时，QP2=62+t2，QB=8−t；
解得，t=74；
③当BP=BQ时，PB2=62+(8−2t)2，QB=8−t；
整理得，3t2−16t+36=0，Δ=256−36×12<0；
∴无解．
综上所述，满足条件的t的值为83或74．
【解析】(1)根据题意画出图形即可．
(2)构建方程求解即可．
(3)分三种情形，分别构建方程求解即可．
本题考查作图−应用与设计作图，坐标与图形变化−平移，等腰三角形的判定和性质，勾股定理等知识，解题的关键是理解题意，灵活运用所学知识解决问题．x
…
0
1
2
3
4
…
y
…
4
1
0
1
4
…