2023年河南省信阳市光山县慧泉中学九年级一模数学检测卷（含答案）

2023年河南省信阳市光山县慧泉中学九年级一模数学检测卷（二）

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．若等腰三角形一个角为，那么它的底角为（    ）

A． B． C．或 D．

2．在扇形统计图中，其中四个扇形的圆心角分别是30°，40°，50°，60°，则剩下的扇形是圆的（    ）

A． B． C． D．

3．已知是方程的一个根，则方程的另一个根和c的值分别为（    ）

A．，-1 B．，-1 C．，1 D．，1

4．如图，在平面直角坐标系中，，，，，…根据这个规律，点的坐标是（    ）

A． B． C． D．

5．抛物线的顶点坐标(　　)

A．(-4，1) B．(-4，-1) C．(4，-1) D．(4，1)

6．抛物线的对称轴为直线．若关于x的一元二次方程（t为实数）在的范围内有实数根，则t的取值范围是（    ）

A． B． C． D．

7．如图，是的直径，，是上的两点，且，则的度数为（    ）

A．42° B．84° C．90° D．96°

8．如图，若BC=EC，∠BCE=∠ACD，则添加不能使△ABC≌△DEC的条件是（  ）

A．AB=DE                               B．∠B=∠E                             C．AC=DC                                            D．∠A=∠D

9．A、B两地相距500 km，大客车以每小时60 km的速度从A地驶向B地，2小时后，小汽车以每小时90 km的速度沿着相同的道路行驶，设小汽车出发x小时后追上大客车，根据题意可列方程为 （　 　）

A．60（x+2）=90x B．60x=90（x-2）

C．60（x+2）+90x=500 D．6x+90（x-2）=500

10．如图所示，在中，．DE垂直平分AB，交BC于点E．若．则（    ）

A．3cm B．4cm C．5cm D．10cm

二、填空题

11．抛物线开口方向是 _____．

12．如图，点O在直线AB上，射线OD平分∠AOC，若∠AOD=20°，则∠COB的度数为_____度．

13．在①长方体、②球、③圆锥、④圆柱、⑤正方体、⑥三棱柱这六种几何体中，其主视图、左视图、俯视图都完全相同的是________（填上序号即可）．

14．2021加上它的得到一个数，再加上所得的数的又得到一个数，再加上这次得数的又得到一个数…，以此类推，一直加到上一次得数的，最后得到的数是__________．

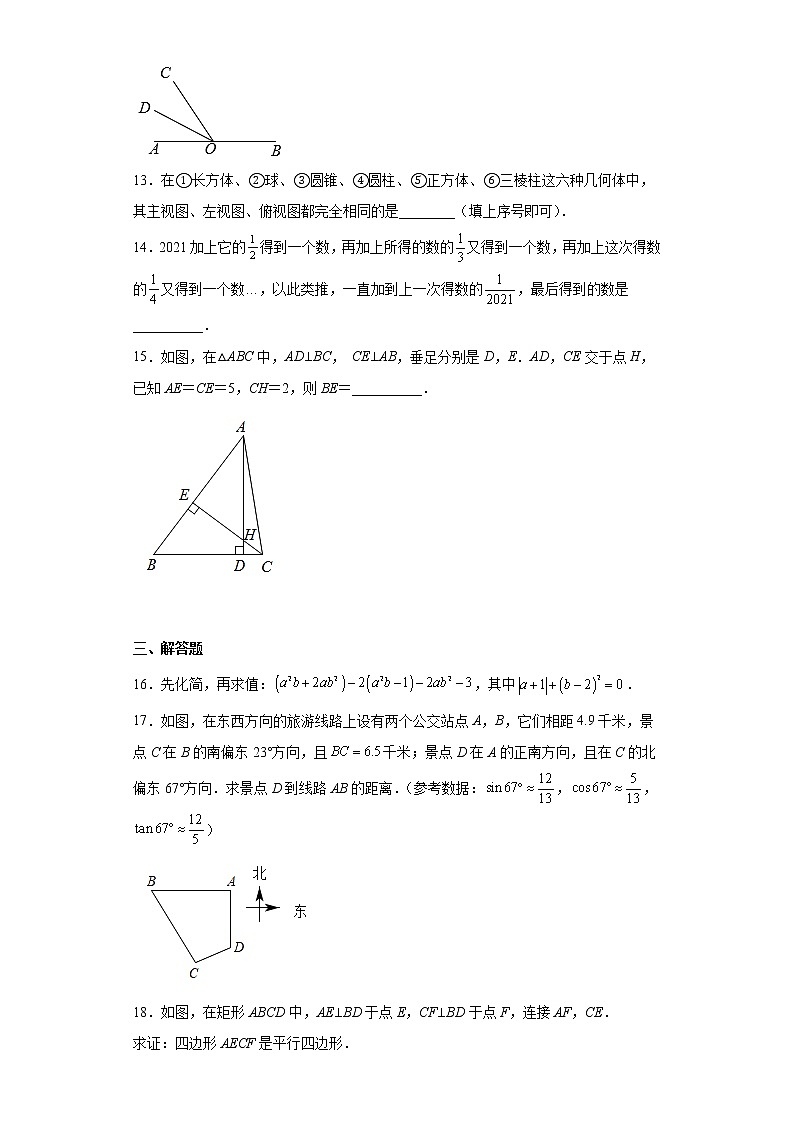
15．如图，在△ABC中，AD⊥BC， CE⊥AB，垂足分别是D，E．AD，CE交于点H，已知AE＝CE＝5，CH＝2，则BE＝__________．

三、解答题

16．先化简，再求值：，其中．

17．如图，在东西方向的旅游线路上设有两个公交站点A，B，它们相距4.9千米，景点C在B的南偏东23°方向，且千米；景点D在A的正南方向，且在C的北偏东67°方向．求景点D到线路AB的距离．（参考数据：，，）

18．如图，在矩形ABCD中，AE⊥BD于点E，CF⊥BD于点F，连接AF，CE．

求证：四边形AECF是平行四边形．

19．请把以下推理过程填写完整：

已知：如图，∠1＝∠2，∠3+∠4＝180°，求证：ac．

证明：∵∠1＝∠2（已知），

∴　　　　（　内错角相等，两直线平行　）．

∵∠3+∠4＝180°（已知），

∴bc（    ）．

∴ac（    ）．

20．在做解方程练习时，有一个方程“yy+■”，题中■处不清晰，李明问老师，老师只是说：“■是一个有理数，该方程的解与当x＝2时整式5（x﹣1）﹣2（x﹣2）﹣4的值相同．”依据老师的提示，请你帮李明找到“■”这个有理数，并求出方程的解．

21．若不等式的解集中，x的每一个值都能使关于x的不等式3（x-1）+5>5x+2（m +x）成立，求m的取值范围．

22．如图，在△ABC中，AB＝AC，D是BC中点，DE⊥AC，垂足为E．若∠BAC＝50°，求∠ADE的度数．

23．列方程（组）解应用题：

平谷区某食用菌种植合作社将废弃树枝秸秆粉碎后制作成蘑菇菌棒．废菌棒经过高温灭虫后还田，生产性废料循环利用还可以改善土壤PH值（土壤酸碱度）和板结的情况，抑制杂草生长，改善蔬果口感．合作社积极鼓励村民用废弃树枝秸秆换取菌棒，培训推广科学种植菌菇技术，扩大种植规模，让更多的村民能够拥有一技之长，形成一条绿色循环生态产业链，实现生态效益与经济效益双赢．现合作社准备购进一批加工菌棒的设备，现有A，B两种型号的设备，经调查购买一台A型号的设备比购买一台B型号的设备多2万元；购买2台A型号的设备比购买3台B型号的设备少1万元．求A，B两种型号的设备每台各多少万元？

参考答案：

1．C

【分析】分类讨论这个的角是等腰三角形的顶角（利用三角形内角和求）还是底角．

【详解】解：若的角是顶角，则底角是，

若的角是底角，则底角是，

则它的底角是或，

故选择：A．

【点睛】本题考查等腰三角形的性质，解题的关键是掌握等腰三角形的性质．

2．A

【分析】根据圆周角等于360°计算即可．

【详解】解：360°-30°-40°-50°-60°=180°，

180°÷360°，

即剩下的扇形是圆的．

故选：A．

【点睛】本题考查了扇形统计图，掌握扇形统计图的定义是解答本题的关键．

3．C

【分析】根据根与系数的关系即可求得方程的另一个根，进而根据求得的值

【详解】是方程的一个根，设另一个根为，，

则

，

故选C

【点睛】本题考查了一元二次方程根与系数的关系，掌握根与系数的关系是解题的关键．

4．C

【分析】根据图形，找到点的坐标变换规律：横坐标依次为、、、、、，纵坐标依次为、、、、，四个一循环，进而求解即可．

【详解】解：观察图形可知，横坐标依次为、、、、、，纵坐标依次为、、、、，四个一循环，

∵，

∴点的坐标是．

故选：C

【点睛】本题考查了点的坐标规律探究，找到点的坐标变换规律是解本题的关键．

5．D

【分析】已知抛物线解析式为顶点式，即可直接写出顶点坐标．

【详解】解：∵，

∴其顶点坐标为(4，1)，

故选D．

【点睛】本题考查二次函数的性质．掌握二次函数，其顶点坐标是(h，k)，对称轴是直线x=h是解题关键．

6．D

【分析】由抛物线的对称轴可得抛物线解析式，将x2+bx+3﹣t＝0转化为抛物线y＝x2+bx+3与直线y＝t在﹣1＜x＜3的范围内有交点的问题，进而求解．

【详解】解：∵抛物线y＝x2+bx+3的对称轴为直线x＝＝1，

∴b＝﹣2，

∴y＝x2﹣2x+3，

∵y＝x2﹣2x+3＝（x﹣1）2+2，

∴抛物线开口向上，顶点坐标为（1，2），

将x2+bx+3﹣t＝0整理为x2﹣2x+3＝t，

∴当t＝2时，抛物线顶点落在直线y＝2上，满足题意，

把（﹣1，t）代入y＝x2﹣2x+3得t＝6，

把（3，t）代入y＝x2﹣2x+3得t＝6，

∴2≤t＜6满足题意，

故选：D．

【点睛】本题考查二次函数的性质，解题关键是掌握二次函数与方程的关系，掌握二次函数图像与系数的关系．

7．B

【分析】根据圆周角定理求出，即可求解．

【详解】解：，

由圆周角定理得：，

故选：B．

【点睛】本题考查了圆周角定理，解题的关键是理同圆中，同弧对应的圆周角等于圆心角的一半．

8．A

【分析】已知条件中已经有一边一角，需要证明全等，再可以添加角，也可以添加边，若添加边，只能添加AC=DC，若添加角，另两组角随便添加即可．

【详解】解：∵∠BCE=∠ACD，

∴∠BCE+∠ACE=∠ACD+∠ACE，

∴∠ACB=∠DCE，

A、根据BC=CE，AB=DE，∠ACB=∠DCE不能推出△ABC≌△DEC，故本选项符合题意；

B、因为∠ACB=∠DCE，∠B=∠E，BC=CE，所以符合AAS定理，即能推出△ABC≌△DEC，故本选项不符合题意；

C、因为BC=CE，∠ACB=∠DCE，AC=CD，所以符合SAS定理，即能推出△ABC≌△DEC，故本选项不符合题意；

D、因为∠A=∠D，∠ACB=∠DCE，BC=CE，所以符合AAS定理，即能推出△ABC≌△DEC，故本选项不符合题意；

故选A．

【点睛】本题考查了三角形全等的判定，掌握三角形的判定定理是解题的关键．

9．A

【分析】根据小汽车追上大客车时，所行驶的路程相等，即可建立等式．

【详解】设小汽车出发x小时后追上大客车，

则追上大客车时，走过的路程为：km，

此时，大客车走过的路程为：km，

则：,

故选：A．

【点睛】本题考查一元一次方程的实际应用问题，抓住追上时各自走过的路程相等建立等式是解决问题的关键．

10．C

【分析】根据线段垂直平分线的性质得AE=BE=10cm，再根据等边对等角和三角形的外角性质求得∠AEC=30°，然后利用含30°角的直角三角形的性质求解即可．

【详解】解：∵DE垂直平分AB，BE=10cm，

∴AE=BE=10cm，

∴∠EAB=∠B=15°，

∴∠AEC=2∠B=30°，

在Rt△ACE中，∠ACE=90°，

∴AC= AE=5cm，

故选：C．

【点睛】本题考查线段垂直平分线的性质、等腰三角形的性质、三角形的外角性质、含30°角的直角三角形的性质，熟练掌握相关知识的联系与运用是解答的关键．

11．向下

【分析】根据题目中的抛物线解析式，可以直接写出该抛物线的开口方向．

【详解】解：∵抛物线，a＝﹣3＜0，

∴该抛物线的开口向下，

故答案为：向下．

【点睛】本题主要考查了二次函数的图象和性质，熟练掌握二次函数的图象和性质是解题的关键．

12．140

【详解】解：∵OD平分∠AOC，

∴∠AOC=2∠AOD=40°，

∴∠COB=180°﹣∠COA=140°

故答案为：140

13．②⑤

【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形判断出各图形的三视图即可得到答案．

【详解】解：①长方体主视图是长方形、左视图是长方形、俯视图也是长方形，但是长方形的边长不一样长；

②球主视图、左视图、俯视图都是圆；

③圆锥主视图、左视图都是三角形．；俯视图是带圆心的圆；

④圆柱主视图、左视图都是长方形，俯视图是圆；

⑤正方体主视图、左视图、俯视图都是正方形；

⑥三棱柱主视图是长方形，中间还有一条竖线；左视图是长方形，俯视图是三角形；

故答案为②⑤．

【点睛】本题主要考查了几何体的三种视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中．

14．2043231

【分析】根据，，，，总结出相应的规律进行求解即可得到答案．

【详解】解：，

，

，

，

…

，

∴当时，

故答案为：2043231．

【点睛】此题考查了数字型规律，学生首先要会根据题意列式，解答时，总结规律解答很关键．

15．3

【分析】由AD垂直于BC，CE垂直于AB，利用垂直的定义得到一对角为直角，再由一对对顶角相等，利用三角形的内角和定理得到一对角相等，再由一对直角相等，以及一对边相等，利用AAS得到△AEH与△EBC全等，由全等三角形的对应边相等和线段的和差即可得出结论．

【详解】解：∵AD⊥BC，CE⊥AB，

∴∠ADB=∠AEH=90°，

∵∠AHE=∠CHD，

∴∠BAD=∠BCE，

∵在△HEA和△BEC中，

∴△HEA≌△BEC（AAS），

∴BE=EH，

∵AE＝CE＝5，CH＝2，

∴BE=EH=CE-CH=3，

故答案为：3．

【点睛】此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．

16．；．

【分析】根据去括号、合并同类项，可化简整式；根据绝对值和偶次幂的非负性，得到a＝－1， b＝2，代入求值可得到答案．

【详解】解：，

，

，

∵，，

∴，，

∴，，

将，代入原式得：

原式=，

答：原式的值为．

【点睛】本题考查了绝对值和偶次幂的非负性质，整式的加减化简求值，去括号与合并同类项法则是解题的关键．

17．5千米

【分析】过点C作交于点M，过点D作于点N，则四边形MADN为矩形，解Rt△BCM可得BM、CM，进而求得AM、DN，解Rt△DNC可得NC，进而求得MN便可解答；

【详解】解：如图，过点C作交于点M，过点D作于点N，

C在B的南偏东23°方向，则∠CBA=90°-23°=67°，

D在C的北偏东67°方向，则∠DCM=67°，

∵景点D在A的正南方向，

∴，

又∵，，

∴四边形MADN为矩形，

∴，，

在中，，千米，

由得（千米），

由得（千米），

∴千米，

∴千米，

在中，，

由得（千米），

∴千米，

∴千米，

∴景点D到线路AB的距离为5千米；

【点睛】本题考查了方位角，矩形的判定和性质，解直角三角形；通过作辅助线构造直角三角形是解题关键．

18．见解析．

【分析】由矩形的性质得出AB＝CD，ABCD，证明△ABE≌△CDF（AAS），由全等三角形的性质得出AE＝CF，由平行四边形的判定可得出结论．

【详解】证明：∵AE⊥BD，CF⊥BD，

∴∠AEB＝∠DFC＝∠AEF＝∠CFE＝90°，

∴AECF

∵四边形ABCD是矩形，

∴AB＝CD，ABCD，

∴∠ABE＝∠FDC，

在△ABE和△CDF中，

∴△ABE≌△CDF（AAS），

∴AE＝CF，

∴四边形AECF为平行四边形；

【点睛】本题考查了矩形的性质，全等三角形的判定与性质，平行四边形的判定，熟记各性质与平行四边形的判定是解题的关键．

19．；；同旁内角互补，两直线平行；平行于同一条直线的两条直线互相平行

【分析】根据平行线的判定定理解答即可．

【详解】解：∵∠1＝∠2（已知），

∴ab（内错角相等，两直线平行）．

∵∠3+∠4＝180°（已知），

∴bc（同旁内角互补，两直线平行 ）．

∴ac（平行于同一条直线的两条直线互相平行）．

【点睛】本题考查了平行线的判定，解题的关键是掌握平行线的判定定理：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行；平行于同一条直线的两条直线互相平行．

20．“■”这个有理数为，方程的解为：y＝1

【分析】利用“该方程的解与当x＝2时整式5（x−1）−2（x−2）−4的值相同”求出方程的解；再将方程的解代入yy+■中求得■．

【详解】解：当x＝2时，整式5（x−1）−2（x−2）−4＝5×（2−1）−2×（2−2）−4＝1．

∵方程的解与当x＝2时整式5（x−1）−2（x−2）−4的值相同，

∴方程的解为：y＝1．

当y＝1时，yy+■．

∴1+■

解得：■＝．

答：“■”这个有理数为，方程的解为：y＝1．

【点睛】本题主要考查了一元一次方程的解，求代数式的值．利用方程的解的意义，将方程的解去替换未知数的值是解题的关键．

21．

【分析】先解得不等式的解集，再解得不等式3（x-1）+5>5x+2（m +x）的解集，得到关于m的不等式即可求得m的取值范围．

【详解】解：解不等式得x，

解不等式得x<.

由题意可知>,

解得m<-

【点睛】本题考查了解一元一次不等式（组）及不等式解集的定义，熟记“同大取大，同小取小，大小小大中间找，大大小小解不了”是解题的关键．

22．65°

【分析】首先根据等腰三角形的三线合一的性质得到AD平分∠BAC，然后求得∠DAC的度数，从而求得答案．

【详解】解：∵AB＝AC，D为BC的中点，

∴∠BAD＝∠CAD，

∵∠BAC＝50°，

∴∠DAC＝25°，

∵DE⊥AC，

∴∠ADE＝90°﹣25°＝65°．

【点睛】本题考查了等腰三角形的性质和直角三角形的两锐角互余，解题的关键是了解等腰三角形三线合一的性质．

23．A型号设备7万元/台，B型号设备5万元/台

【分析】由题意，设A型号设备x万元/台，B型号设备y万元/台，然后列出方程组，解方程组即可得到答案．

【详解】解：设A型号设备x万元/台，B型号设备y万元/台．

根据题意列方程组，得：              

解方程得：．                     

答：A型号设备7万元/台，B型号设备5万元/台．

【点睛】本题考查了二元一次方程组的应用，解题的关键是熟练掌握题意，正确的理解题意，从而进行解题．