2024-2025学年河北省邯郸市高二上学期开学考试数学试卷（含解析）

这是一份2024-2025学年河北省邯郸市高二上学期开学考试数学试卷（含解析），共18页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

1.已知向量m，n满足m=n=2，且m⋅n=−2 2，则m，n夹角为( )
A. π6B. π4C. 3π4D. 5π6
2.在▵ABC中，角A,B,C对边为a,b,c，且2c⋅cs2A2=b+c，则▵ABC的形状为( )
A. 等边三角形B. 直角三角形C. 等腰三角形D. 等腰直角三角形
3.设复数z1=4+2i，z2=1−3i，则复数z2−z12的虚部是( )
A. 4iB. −4iC. 4D. −4
4.袋中装有红、黄、蓝三种颜色的球各2个，无放回的从中任取3个球，则恰有两个球同色的概率为
A. 15B. 310C. 35D. 45
5.若双曲线x2a2−y2b2=1a>0,b>0的一条渐近线方程为y=−2x，该双曲线的离心率是( )
A. 52B. 3C. 5D. 2 3
6.在四面体ABCD中，AB=AC=2 3，BC=6，AD⊥平面ABC，四面体ABCD的体积为 3.若四面体ABCD的顶点均在球O的表面上，则球O的表面积是( )．
A. 49π4B. 49πC. 49π2D. 4π
7.已知圆C1：(x+5)2+y2=1，C2：(x−5)2+y2=225，动圆C满足与C1外切且C2与内切，若M为C1上的动点，且CM⋅C1M=0，则CM的最小值为
A. 2 2B. 2 3C. 4D. 2 5
8.已知E，F分别是棱长为2的正四面体ABCD的对棱AD,BC的中点.过EF的平面α与正四面体ABCD相截，得到一个截面多边形τ，则下列说法正确的是( )
A. 截面多边形τ不可能是平行四边形
B. 截面多边形τ的周长是定值
C. 截面多边形τ的周长的最小值是 2+ 6
D. 截面多边形τ的面积的取值范围是1, 2
二、多选题：本题共3小题，共15分。在每小题给出的选项中，有多项符合题目要求。
9.下列结论中正确的是( )
A. 在频率分布直方图中，中位数左边和右边的直方图的面积相等
B. 一组数据中的每个数都减去同一个非零常数a，则这组数据的平均数改变，方差不改变
C. 一个样本的方差s2=120[(x1−3)2+(x2−3)2+⋯+(x20−3)2]，则这组样本数据的总和等于60
D. 数据a1，a2，a3，...，an的方差为M，则数据2a1，2a2，2a3，…，2an的方差为2M
10.设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是( )
A. 若m⊂α，n⊂α，m//β，n//β，则α//β
B. 若m⊥n，m//α，α//β，则n⊥β
C. 若m，n异面，m⊂α，m//β，n⊂β，n//α，则α//β
D. 若α//β，m⊥α，n//β，则m⊥n
11.如图，已知在平行四边形ABCD中，AB=2AD=2，∠BAD=60°，E为AB的中点，将△ADE沿直线DE翻折成△PDE，若M为PC的中点，则△ADE在翻折过程中(点P∉平面ABCD)，以下命题正确的是( )
A. BM //平面PDE
B. BM= 32
C. 存在某个位置，使MB⊥DE
D. 当三棱锥P—CDE体积最大时，其外接球的表面积为13π3
三、填空题：本题共3小题，每小题5分，共15分。
12.某学校三个年级共有2760名学生，要采用分层抽样的方法从全体学生中抽取一个容量为60的样本，已知一年级有1150名学生，那么从一年级抽取的学生人数是 名.
13.设双曲线C：x24−y221=1的左焦点和右焦点分别是F1，F2，点P是C右支上的一点，则PF1+3PF2的最小值为 ．
14.已知点P是椭圆C:x26+y24=1上除顶点外的任意一点，过点P向圆O:x2+y2=4引两条切线PM，PN，设切点分别是M，N，若直线MN分别与x轴，y轴交于A，B两点，则▵AOB面积的最小值是 ．
四、解答题：本题共5小题，共60分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题12分)
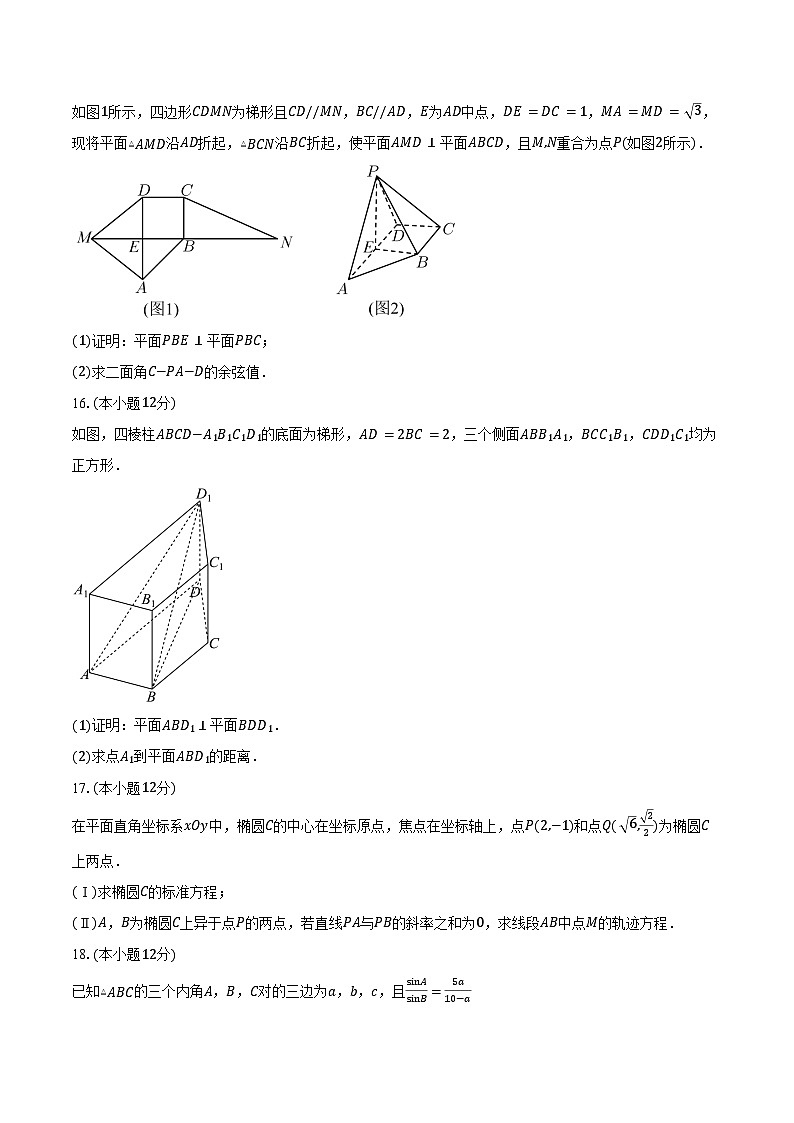
如图1所示，四边形CDMN为梯形且CD//MN，BC//AD，E为AD中点，DE=DC=1，MA=MD= 3，现将平面▵AMD沿AD折起，▵BCN沿BC折起，使平面AMD⊥平面ABCD，且M,N重合为点P(如图2所示)．
(1)证明：平面PBE⊥平面PBC；
(2)求二面角C−PA−D的余弦值．
16.(本小题12分)
如图，四棱柱ABCD−A1B1C1D1的底面为梯形，AD=2BC=2，三个侧面ABB1A1，BCC1B1，CDD1C1均为正方形．

(1)证明：平面ABD1⊥平面BDD1．
(2)求点A1到平面ABD1的距离．
17.(本小题12分)
在平面直角坐标系xOy中，椭圆C的中心在坐标原点，焦点在坐标轴上，点P(2,−1)和点Q( 6, 22)为椭圆C上两点．
(Ⅰ)求椭圆C的标准方程；
(Ⅱ)A，B为椭圆C上异于点P的两点，若直线PA与PB的斜率之和为0，求线段AB中点M的轨迹方程．
18.(本小题12分)
已知▵ABC的三个内角A，B，C对的三边为a，b，c，且sinAsinB=5a10−a
(1)若b=1，A=π3，求sinB；
(2)已知C=π3，当S▵ABC取得最大值时，求▵ABC的周长．
19.(本小题12分)
如图，ABCD为圆柱OO′的轴截面，EF是圆柱上异于AD，BC的母线．
(1)证明：BE⊥平面DEF；
(2)若AB=BC= 6，当三棱锥B−DEF的体积最大时，求二面角B−DF−E的正弦值．
答案解析
1.C
【解析】根据向量的点乘关系，求出csθ，即可求出m，n夹角．
解：由题意，
在向量m，n中，m=n=2，
m⋅n=mncsθ=2×2csθ=4csθ=−2 2
解得：csθ=− 22
∴θ=34π
故选：C．
2.B
【解析】解：因为2c⋅cs2A2=b+c，
所以2c⋅1+csA2=b+c，即c+ccsA=b+c，
所以ccsA=b，
在▵ABC中，
由余弦定理推论：csA=b2+c2−a22bc，
代入得，c⋅b2+c2−a22bc=b，即b2+c2−a2=2b2，
所以c2=a2+b2，
所以▵ABC 是直角三角形．
故选：B．
3.D
【解析】z2−z12=(1−3i)−4+2i2=−1−4i，
则其虚部是−4。
故选：D．
4.C
【解析】解：从红、黄、蓝三种颜色的球各2个，无放回的从中任取3个球，共有C63=20种，其中恰有两个球同色有C31⋅C41=12种，故恰有两个球同色的概率为P=1220=35．
故选：C．
5.C
【解析】双曲线的焦点位于x轴，则双曲线的渐近线为y=±bax，
因为双曲线的一条渐近线方程为y=−2x，
所以ba=2，
所以双曲线的离心率为e=ca= a2+b2a2= 1+b2a2= 5，
故选：C
6.B
【解析】因为AB=AC=2 3，BC=6，
所以cs∠BAC=AB2+AC2−BC22AB⋅AC=−12，则sin∠BAC= 1−cs2∠BAC= 32，
则S▵ABC=12⋅AB⋅AC⋅sin∠BAC=12⋅2 3⋅2 3⋅ 32=3 3，
因为AD⊥平面ABC，四面体ABCD的体积为 3，
所以 3=13⋅S▵ABC⋅AD= 3AD，则AD=1；
设▵ABC的外接圆半径为r，记▵ABC外接圆圆心为O1，连接AO1，
由正弦定理可得，2r=BCsin∠BAC=6 32=4 3，则AO1=r=2 3
设外接球的半径为R，连接OO1，
根据球的性质可得，OO1⊥平面ABC，
又AD⊥平面ABC，所以AD//OO1，
延长O1O到E，使得O1E=AD，连接DE，
则四边形AO1ED为矩形；所以AO1=DE
连接OA，OD，则OA=OD=R，
所以Rt▵DEO≃Rt▵AO1O，所以OO1=OE=12AD=12，
因此R=OA= AO 12+OO 12= r2+14= 12+14= 494，
因此球O的表面积是S=4πR2=49π．
故选：B．
7.A
【解析】
∵圆C1：x+52+y2=1，圆C2：x−52+y2=225，
动圆C满足与C1外切且C2与内切，设圆C的半径为r，
由题意得CC1+CC2=1+r+15−r=16,∴则C的轨迹是以(−5,0,5,0为焦点，长轴长为16的椭圆，
∴其方程为x264+y239=1,因为CM⋅C1M=0，即CM为圆C1的切线，要CM的最小，只要CC1最小，设Mx0,y0，则CM= CC1⇀2−12= x0+52+y02−1= x02+10x0+25+391−x0264−1
= 25x0264+10x0+64−1,∵−8≤x0≤8,∴CMmin= 25−8264+10×−8+64−1=2 2. ，选A．
8.D
【解析】对于A，当平面α过AD或BC时，截面为三角形．
易知正四面体关于平面ADF对称，将平面α从平面ADF开始旋转与AB交于点G时，
由对称性可知，此时平面α与CD交于点H，且AG=DH，
此时截面为四边形EGFH，且注意到当G,H分别为AB,CD的中点时，此时满足AG=DH，
且GF//AC,AC//EH,GF=EH=12AC，即此时截面四边形EGFH是平行四边形，故 A错误；

对于BC，设AG=m0≤m≤2，由余弦定理得GE= m2+1−m= m−122+34，
GF= 2−m2+1−2−m= m−322+34，
由两点间距离公式知，GE+GF表示动点m,0到定点12, 32和32,− 32的距离之和，
当三点共线时取得最小值 12−322+ 32+ 322=2，
由二次函数单调性可知，当m=0或m=2时，GE+GF取得最大值1+ 3，
所以截面多边形τ周长的取值范围是4,2+2 3，故 BC错误；
对于D，记GH与EF的交点为O，由对称性∠EFG=∠EFH，FG=FH，
所以EF⊥GH，SEGFH=12EF⋅GH，
因为AF= AB2−BF2= 3，
所以EF= AF2−AE2= 2，所以SEGFH= 22GH，
记AB=a,AC=b,AD=c，
则GH=GA+AD+DH=−m2a+c+m2b−c=−m2a+m2b+1−m2c，
因为a⋅b=a⋅c=b⋅c=2×2csπ3=2,a=b=c=2，
所以GH2=m24a2+m24b2+1−m22c2−m2a⋅b−m1−m2a⋅c+m1−m2b⋅c
=m2+m2+41−m22−m2−2m1−m2+2m1−m2
=2m−12+2，
由二次函数性质可知，2≤GH2≤4，即 2≤GH≤2，
所以1≤SEGFH≤ 2，故 D正确；
故选：D
9.ABC
【解析】对于A，在频率分布直方图中，中位数左边和右边的直方图的面积相等，都为12，∴A正确：
对于B，一组数据中的每个数都减去同一个非零常数a，则这组数据的平均数也减去a，方差s2不改变，∴B正确；
对于C，∵样本的方差s2=120[(x1−3)2+(x2−3)2+⋯+(x20−3)2]，∴这个样本有20个数据，平均数是3，∴这组样本数据的总和为3×20=60，C正确；
对于D，数据a1，a2，a3，…，an的方差为M，则数据2a1，2a2，2a3，…，2an的方差为4M，∴D不正确．
故选：ABC
10.CD
【解析】解：对于A：当且仅当m与n相交时，满足α//β，故 A错误；
对于B：若m⊥n，m//α，α//β，则n//β或n⊂β，或n与β相交，故 B错误；
对于C：假设α与β不平行，即α与β相交，设α∩β=l，
若l与m、n不重合，由m⊂α，m//β，所以l//m，又n⊂β，n//α，所以l//n，所以m//n，与m，n异面矛盾，故假设不成立，
若l与m、n中某一条直线重合，则直接可以得到m//n，与m，n异面矛盾，故假设不成立，故 C正确；
对于D：若α//β，m⊥α，则m⊥β，又n//β，所以m⊥n，故 D正确；
故选：CD
11.ABD
【解析】解：如图，取CD的中点N，连接MN，BN，
∵M，E分别为PC，AB的中点，
∴MN//PD，BN//DE．
易证MN//平面PDE，BN//平面PDE．
∵MN∩BN=N， MN， BN⊂平面 BMN，
∴平面 BMN//平面 PDE.又 BM⊂平面 BMN，
∴ BM // 平面PDE，即A正确；
由A可知，MN=12PD=12AD=12，BN=DE=AD=1，
∴∠MNB=∠PDE=∠ADE=60∘，
在 ▵BMN中，由余弦定理知，
BM2=MN2+BN2−2MN⋅BN⋅cs∠MNB=34，
∴BM= 32，是定值，即B正确；
取PD的中点G，则四边形BMGE为平行四边形，
若存在某个位置，使MB⊥DE，则EG⊥DE，与条件矛盾，故C错误；
当三棱锥 P−CDE的体积最大时，
平面 PDE⊥平面 CDE，平面 PDE∩平面 CDE=DE，
又 CE⊥DE，CE⊂平面 CDE，∴ CE⊥平面 PDE，
设三棱锥C−PDE的外接球的球心为O，
O在平面PDE上的射影是正三角形PDE的中心，O到平面PDE的距离等于12CE，
则外接球的半径 OE= 332+ 322= 1312，
∴外接球的表面积 S=4π× 13122=13π3，故D正确，
故选ABD．
12.25
【解析】由分层抽样得从一年级抽取的学生人数是602760×1150=25人.
故答案为：25．
13.8
【解析】a=2,b= 21,c=5，PF2≥c−a=3,PF1=PF2+2a=PF2+4，
PF1+3PF2=PF2+3PF2+4,PF2≥3，
而函数y=x+3x+4,x>0在3,+∞上单调递增，
所以当且仅当x=3时，ymin=8．
故答案为：8．
14.4 63
【解析】解：设Px0,y0,x0y0≠0，
则以OP为直径的圆的方程为x2+y2−x0x−y0y=0，
与圆O:x2+y2=4的方程相减得x0x+y0y−4=0，
即x0x+y0y−4=0是过切点M,N的直线方程，
则A(4x0,0),B(0,4y0)，
所以S△OAB=12·4x0·4y0=8|x0y0|，
又因为在点P在椭圆C:x26+y24=1上，
所以x026+y024=1，即24=4x02+6y02≥4 6x0y0，
所以x0y0≤ 6，当且仅当4x02=6y02，即x02=3,y02=2时取等号，
所以S▵OAB=8x0y0≥8 6=4 63，
即▵AOB面积的最小值是4 63．

15.(1)
证明：因为MA=MD= 3，
即PA=PD= 3，E为AD的中点，
所以▵PAD是等腰三角形，
且ME⊥AD，即PE⊥AD，
又因为平面AMD⊥平面ABCD，且平面AMD∩平面ABCD=AD，PE⊂平面PAD，
所以PE⊥平面ABCD，又BC⊂平面ABCD，
所以PE⊥BC，
又因为CD//MN，且ME⊥AD，
所以四边形NCDE为直角梯形，且DE=DC=1，
所以四边形BCDE是正方形，所以BC⊥EB，
又因为PE∩EB=E，
所以BC⊥平面PBE，又因为BC⊂平面PBC，
所以平面PBE⊥平面PBC；
(2)
由(1)知：以E为原点，EA，EB，EP为x，y，z轴，建立如图所示空间直角坐标系：
则A1,0,0,D−1,0,0,C−1,1,0,P0,0, 2，，
所以PA=1,0,− 2,PC=−1,1,− 2,PD=−1,0,− 2，
设平面PAC的一个法向量为m=x,y,z，
则，即x− 2z=0−x+y− 2z=0,
令z= 2，则m=2,4, 2，
易知平面PAD的一个法向量为n=0,1,0，
则csm,n=m⋅nm⋅n=4 22=2 2211，
所以二面角C−PA−D的余弦值是2 2211．
【解析】(1)易证PE⊥AD，再由平面AMD⊥平面ABCD，得到PE⊥平面ABCD，则PE⊥BC，再由四边形BCDE是正方形，得到BC⊥EB，然后利用线面垂直和面面垂直的判定定理证明；
(2)以E为原点，EA，EB，EP为x，y，z轴，建立空间直角坐标系，求得平面PAC的一个法向量m=x,y,z，易知平面PAD的一个法向量为n=0,1,0，然后由csm,n=m⋅nm⋅n求解．
16.(1)
因为侧面ABB1A1，BCC1B1，CDD1C1均为正方形，所以B1B⊥AB，B1B⊥BC，AB=CD．
又AB∩BC=B，AB,BC⊂面ABCD，所以B1B⊥面ABCD．
由棱柱的性质，四棱柱为直四棱柱，则DD1⊥面ABCD，又AB⊂面ABCD，则D1D⊥AB．
又四边形ABCD为梯形，AB=CD，AD=2BC=2，所以AD//BC．
过点C作CE⊥AD，垂足为E，则DE=12×(2−1)=12CD，

所以∠CDE=60∘，则∠BCD=120∘．
在等腰三角形BCD中BD=2× 12−122= 3．
因为AD2=AB2+BD2，所以AB⊥BD．
因为BD∩D1D=D，BD,D1D⊂面BDD1，所以AB⊥面BDD1．
又AB⊂平面ABD1，所以平面ABD1⊥平面BDD1．
(2)
法一：连接A1B，B1D1，

由(1)直三棱柱ABD−A1B1D1的体积VABD−A1B1D1=S▵ABD×AA1=12×1× 3×1= 32．
由直三棱柱的性质知，三棱锥B−A1B1D1的体积VB−A1B1D1=13VABD−A1B1D1，
三棱锥D1−ABD的体积VD1−ABD=13VABD−A1B1D1，
所以VA1−ABD1=VABD−A1B1D1−VB−A1B1D1−VD1−ABD=13VABD−A1B1D1= 36．
由AB⊥面BDD1，BD1⊂面BDD1，则AB⊥BD1，且BD1= BD2+DD12=2．
设点A1到平面ABD1的距离为d，则VA1−ABD1=13×12×AB×BD1×d= 36，
即13×12×1×2×d= 36，解得d= 32，故点A1到平面ABD1的距离为 32．
法二：因A1B1//AB，且AB⊂面ABD1，面ABD1，所以A1B1//面ABD1，
所以A1，B1两点到平面ABD1的距离相等．
过点B1作B1H⊥BD1，垂足为点H，连接B1D1．

易得B1H⊥平面ABD1，所以线段B1H的长度即为点A1到平面ABD1的距离．
因为BB1=1，B1D1=BD= 3，BD1= BD2+DD12=2，所以B1H= 32．
所以点A1到平面ABD1 距离为 32．
【解析】(1)由题设及线面垂直的判定得B1B⊥面ABCD，进而有D1D⊥AB，过点C作CE⊥AD，垂足为E，进而证AB⊥BD，最后由线面、面面垂直的判定证结论；
(2)法一：连接A1B，B1D1，应用等体积法有VD1−ABD=13VABD−A1B1D1求点面距；法二：证线面平行得到A1，B1两点到平面ABD1的距离相等，过点B1作B1H⊥BD1，垂足为点H，连接B1D1，进而求点面距．
17.解：(Ⅰ)设椭圆的方程为mx2+ny2=1(m>0,n>0,m≠n)，
因为点P(2,−1)和点Q( 6, 22)为椭圆C上两点，
所以4m+n=16m+12n=1，解得m=18,n=12，
故椭圆C的标准方程为x28+y22=1；
(Ⅱ)设PA的斜率为k，所以直线PA的方程为y+1=k(x−2)，即y=k(x−2)−1，
联立方程组y=k(x−2)−1x2+4y2−8=0，可得(x−2)[(1+4k2)x−8k2−8k+2]=0，
所以点A的横坐标为xA=8k2+8k−21+4k2，纵坐标为yA=4k2−4k−11+4k2，
因为直线PA与PB的斜率之和为0，
所以直线PB的斜率为−k，
同理可求出点B的坐标为(8k2−8k−21+4k2,4k2+4k−11+4k2)，
故点M的坐标为(8k2−21+4k2,4k2−11+4k2)，
所以点M的坐标满足x=2y，
由x=2yx2+4y2−8=0，解得x=±2，
所以−2故点M的轨迹方程为x−2y=0(−2【解析】本题考查了椭圆标准方程的求解，直线与椭圆位置关系的应用，在解决直线与圆锥曲线位置关系的问题时，一般会联立直线与圆锥曲线的方程，利用韦达定理和“设而不求”的方法进行研究，属于较难题．
(Ⅰ)利用待定系数法设椭圆的方程为mx2+ny2=1(m>0,n>0,m≠n)，由点在椭圆上，列出关于m，n的方程组，求出m，n，即可得到椭圆C的方程；
(Ⅱ)设PA的斜率为k，得到直线PA的方程，联立直线PA与椭圆的方程，求出点A的坐标，联立直线PB与椭圆的方程，求出点B的坐标，从而得到点M的坐标，消去参数k，即可得到点M的轨迹方程．
18.(1)
∵sinAsinB=5a10−a，
∴ab=5a10−a，
∴a+5b=10，又b=1，
∴a=5，
由正弦定理可知：asinA=bsinB，
∴sinB=1× 325= 310；
(2)
∵S△ABC=12ab⋅sinC= 34ab，当S▵ABC取最大值时，即ab取最大值，
∵a+5b=10，
∴5ab≤(5b+a)24，
∴ab≤(5b+a)220=5，当且仅当a=5b时，即a=5，b=1时等号成立，
由余弦定理可知：csC=a2+b2−c22ab，
∴c= a2+b2−2ab⋅csC= 52+12−2×5×1×12= 21，
∴c= 21
∴▵ABC的周长a+b+c=6+ 21．
【解析】(1)根据正弦定理，化角为边，即可求出a，再利用正弦定理即可求出sinB；
(2)根据基本不等式及三角形面积公式可得面积取得最大值时，对应的a,b的值，再根据余弦定理求出边c，进而得到▵ABC的周长．
19.解：(1)证明：如图，连接AE，由题意知AB为⊙O的直径，
所以AE⊥BE.因为AD，EF是圆柱的母线，
所以AD//EF且AD=EF，所以四边形AEFD是平行四边形．
所以AE//DF，所以BE⊥DF．
因为EF是圆柱的母线，所以EF⊥平面ABE，
又因为BE⊂平面ABE，所以EF⊥BE．
又因为DF∩EF=F，DF、EF⊂平面DEF，所以BE⊥平面DEF．
(2)由(1)知BE是三棱锥B−DEF底面DEF上的高，
由(1)知EF⊥AE，AE/​/DF，所以EF⊥DF，
即底面三角形DEF是直角三角形．
设DF=AE=x，BE=y，
则在Rt△ABE中有：x2+y2=6，
所以VB−DEF=13S△DEF⋅BE=13⋅(12x⋅ 6)⋅y= 66xy≤ 66⋅x2+y22= 62，
当且仅当x=y= 3时等号成立，即点E，F分别是AEB，CFD的中点时，三棱锥B−DEF的体积最大，
下面求二面角B−DF−E的正弦值：
法一：由(1)得BE⊥平面DEF，因为DF⊂平面DEF，所以BE⊥DF．
又因为EF⊥DF，EF∩BE=E，所以DF⊥平面BEF．
因为BF⊂平面BEF，所以BF⊥DF，所以∠BFE是二面角B−DF−E的平面角，
由(1)知△BEF为直角三角形，则BF= ( 3)2+( 6)2=3．
故sin∠BFE=BEBF= 33，所以二面角B−DF−E的正弦值为 33．
法二：由(1)知EA，EB，EF两两相互垂直，
如图，以点E为原点，EA，EB，EF所在直线为x，y，z轴建立空间直角坐标系E−xyz，
则B(0, 3,0),D( 3,0, 6),E(0,0,0),F(0,0, 6)．
由(1)知BE⊥平面DEF，故平面DEF的法向量可取为EB=(0, 3,0)．
设平面BDF的法向量为n=(x,y,z)，
由DF=(− 3,0,0),BF=(0,− 3, 6)，
得n⋅DF=0n⋅BF=0，即− 3x=0− 3y+ 6z=0，即x=0y= 2z，取z=1，得n=(0, 2,1)．
设二面角B−DF−E的平面角为θ，
|csθ|=|cs〈n,EB〉|=|n⋅EB||n|⋅|EB|= 2× 3 3× 3= 63，
所以二面角B−DF−E的正弦值为 33．
【解析】本题考查线面垂直的判定与性质、向量法的应用、二面角的定义及其正弦值的求法，考查运算求解能力等基础知识，考查运算求解能力，是中档题．
(1)连接AE，由题意知AB为⊙O的直径，AE⊥BE，四边形AEFD是平行四边形，从而AE/​/DF，BE⊥DF，由EF是圆柱的母线，得EF⊥平面ABE，EF⊥BE，由此能证明BE⊥平面DEF．
(2)由BE是三棱锥B−DEF底面DEF上的高，EF⊥AE，AE/​/DF，EF⊥DF，底面三角形DEF是直角三角形．设DF=AE=x，BE=y，可确定点E，F分别是AEB，CFD的中点时，三棱锥B−DEF的体积最大，根据二面角的定义或利用空间向量的夹角公式计算，即可求出二面角B−DF−E的正弦值．