江苏省扬州中学教育集团树人学校2021-2022学年七年级上学期期末数学试卷

这是一份江苏省扬州中学教育集团树人学校2021-2022学年七年级上学期期末数学试卷，共17页。试卷主要包含了﹣2的绝对值是 　 　等内容，欢迎下载使用。

一．选择题（本大题共8小题，每题3分，共24分）
1．（3分）﹣2的相反数是（ ）
A．2B．﹣2C．D．
2．（3分）下列计算正确的是（ ）
A．﹣2+3＝5B．﹣7﹣（﹣4）＝﹣3
C．（﹣3）2＝﹣6D．（﹣）÷（﹣8）＝1
3．（3分）据世卫组织2022年1月10日公布的最新统计数据，全球累计确诊新冠肺炎病例约达300000000例，数据300000000用科学记数法表示为（ ）
A．3×108B．3×109C．30×108D．0.3×109
4．（3分）三本相同的书本叠成如图所示的几何体，它的左视图是（ ）
A．B．
C．D．
5．（3分）高速公路的建设带动我国经济的快速发展．在高速公路的建设中，通常要从大山中开挖隧道穿过，把道路取直，以缩短路程．这样做包含的数学道理是（ ）
A．两点确定一条直线
B．两点之间，线段最短
C．两条直线相交，只有一个交点
D．直线是向两个方向无限延伸的
6．（3分）如图，在△ABC中，∠BAC＝90°，∠CDA＝90°，则与∠B互为余角的角有（ ）
A．2个B．3个C．4个D．5个
7．（3分）《算学启蒙》中有一道题，原文是：良马日行二百四十里，驽马日行一百二十里．驽马先行一十二日，问良马几何追及之？译文为：跑得快的马每天走240里，跑的慢的马每天走120里．慢马先走12天，快马几天可以追上慢马？设快马x天可以追上慢马，可列方程（ ）
A．240（x+12）＝120xB．240（x﹣12）＝120x
C．240x＝120（x+12）D．240x＝120（x﹣12）
8．（3分）汉字文化正在走进人们的日常消费生活．如图所示图形都是由同样大小的圆点和线段按照一定的规律排列组成的篆书简化“汉”字，其中，图①中共有12个圆点，图②中共有18个圆点，图③中共有25个圆点，图④中共有33个圆点…依此规律则，图⑩中共有圆点的个数是（ ）
A．63B．75C．88D．102
二．填空题（本大题共10小题，每题3分，共30分）
9．（3分）﹣2的绝对值是 ．
10．（3分）若代数式2xmy2与﹣2xy2n为同类项，则m+n的值为 ．
11．（3分）已知∠A＝38°30'，则∠A的补角的大小是 ．
12．（3分）若x＝2是关于x的方程mx+4＝3m的解，则m＝ ．
13．（3分）如果2a﹣3b的值为﹣1，则6b﹣4a+1的值为 ．
14．（3分）一件商品标价140元，若八折出售，仍可获利12%，则这件商品的进价为 元．
15．（3分）已知点C在线段AB上，AB＝8，BC＝2，M是线段AC的中点，则AM的长为 ．
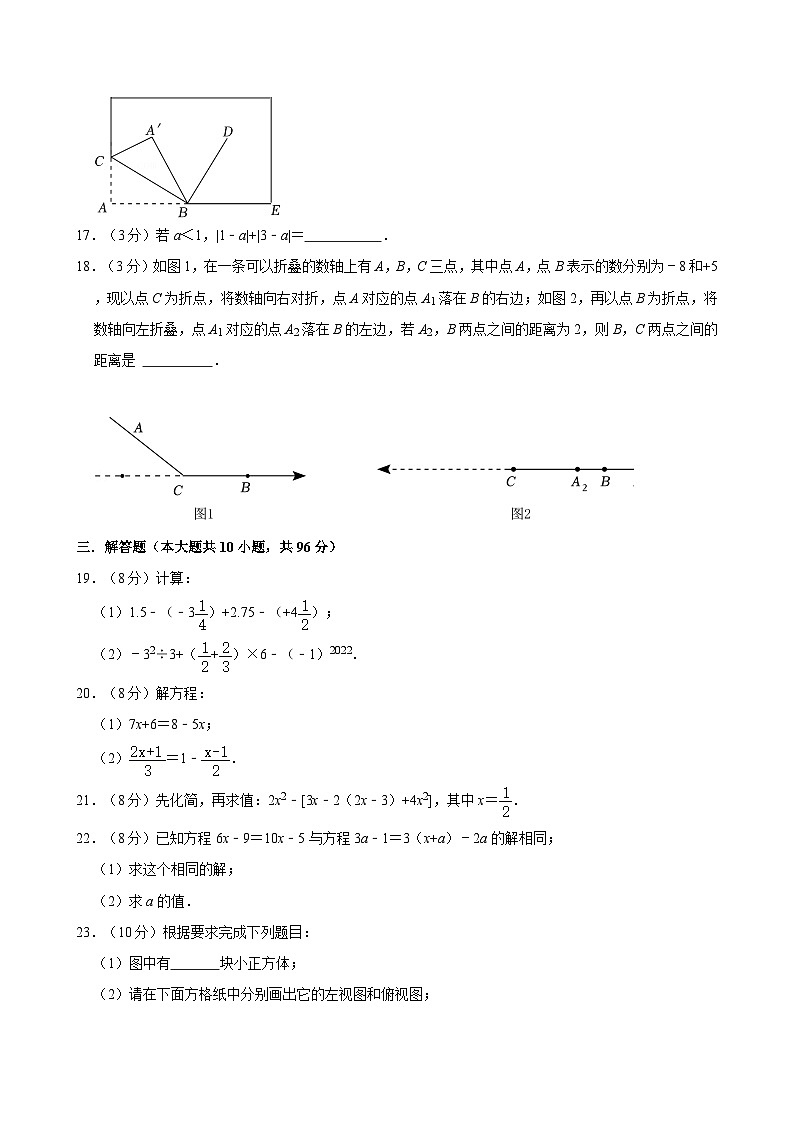
16．（3分）如图，将书页的一角斜折过去，使角的顶点A落在A′处，BC为折痕，BD平分∠A′BE，若∠A′BD＝70°，则∠ABC＝ ．
17．（3分）若a＜1，|1﹣a|+|3﹣a|＝ ．
18．（3分）如图1，在一条可以折叠的数轴上有A，B，C三点，其中点A，点B表示的数分别为﹣8和+5，现以点C为折点，将数轴向右对折，点A对应的点A1落在B的右边；如图2，再以点B为折点，将数轴向左折叠，点A1对应的点A2落在B的左边，若A2，B两点之间的距离为2，则B，C两点之间的距离是 ．
三．解答题（本大题共10小题，共96分）
19．（8分）计算：
（1）1.5﹣（﹣3）+2.75﹣（+4）；
（2）﹣32÷3+（+）×6﹣（﹣1）2022．
20．（8分）解方程：
（1）7x+6＝8﹣5x；
（2）＝1﹣．
21．（8分）先化简，再求值：2x2﹣[3x﹣2（2x﹣3）+4x2]，其中x＝．
22．（8分）已知方程6x﹣9＝10x﹣5与方程3a﹣1＝3（x+a）﹣2a的解相同；
（1）求这个相同的解；
（2）求a的值．
23．（10分）根据要求完成下列题目：
（1）图中有 块小正方体；
（2）请在下面方格纸中分别画出它的左视图和俯视图；
（3）用小正方形体搭一个几何体，使得它的俯视图和左视图与你在如图方格中所画的图一致，则这样的几何最多要 个小正方体．
24．（10分）如图，O在直线AB上，射线OD平分∠AOC，射线OE在∠BOC内．
（1）若∠DOE＝90°，求证：射线OE是∠BOC的平分线；
（2）若∠COE＝∠EOB，∠DOE＝48°，求∠EOB的度数．
25．（10分）在如图所示的方格纸中，每个小正方形的边长为1，每个小正方形的顶点都叫格点，请利用网格特征，解答下列问题
（1）过点C画AB的垂线，并标出垂线所经过的格点E；
（2）过点C画AB的平行线，并标出平行线所经过的格点F；
（3）直线CE与直线CF的位置关系是 ；
（4）连接AC，BC，则△ABC的面积为 ．
26．（10分）扬州树人学校初一年级某班级为了迎接新年，装扮教室，购买了2种气球，气球种类有笑脸和爱心两种．两种气球的价格不同，但同一种类的气球价格相同，由于教室布置需要，购买了的三束气球（每束4个气球），每束价格如图所示．
（1）若笑脸气球的单价是x元，则爱心气球的单价为 元；
（2）请用含x的代数式表示第②束的总价格和第③束气球的总价格；
（3）若第②束气球的总价钱比第③束气球的总价钱少2元，求这两种类的气球的单价．
27．（12分）定义：若m+n＝3，则称m与n是关于3的巧数．
（1）1与 是关于3的巧数，5﹣x与 是关于3的巧数（填一个含x的代数式）；
（2）若a＝x2+6x﹣1，b＝x2﹣2（x2+3x﹣1）+2，判断a与b是否是关于3的巧数，并说明理由；
（3）若c＝kx﹣1，d＝x﹣4，且c与d是关于3的巧数，若x为正整数，求非负整数k的值．
28．（12分）如图，以直线AB上一点O为端点作射线OC，使∠AOC＝48°，在同一个平面内将一个直角三角板的直角顶点放在点O处．（注：∠DOE＝90°）
（1）如图1，如果直角三角板DOE的一边OD放在射线OA上，那么∠COE的度数为 ；
（2）如图2，将直角三角板DOE绕点O按顺时针方向转动到某个位置，如果OC恰好平分∠AOE，求∠COD的度数；
（3）如图3，将直角三角板DOE绕点O任意转动，如果OD始终在∠AOC的内部，请直接用等式表示∠AOD和∠COE之间的数量关系．
参考答案
一．选择题（本大题共8小题，每题3分，共24分）
1．（3分）﹣2的相反数是（ ）
A．2B．﹣2C．D．
【解答】解：﹣2的相反数是：﹣（﹣2）＝2，
故选：A．
2．（3分）下列计算正确的是（ ）
A．﹣2+3＝5B．﹣7﹣（﹣4）＝﹣3
C．（﹣3）2＝﹣6D．（﹣）÷（﹣8）＝1
【解答】解：﹣2+3＝1，故选项A错误，不符合题意；
﹣7﹣（﹣4）＝﹣7+4＝﹣3，故选项B正确，符合题意；
（﹣3）2＝9，故选项C错误，不符合题意；
（﹣）÷（﹣8）＝＝，故选项D错误，不符合题意；
故选：B．
3．（3分）据世卫组织2022年1月10日公布的最新统计数据，全球累计确诊新冠肺炎病例约达300000000例，数据300000000用科学记数法表示为（ ）
A．3×108B．3×109C．30×108D．0.3×109
【解答】解：300000000＝3×108．
故选：A．
4．（3分）三本相同的书本叠成如图所示的几何体，它的左视图是（ ）
A．B．
C．D．
【解答】解：从左面看，是一列三个矩形．
故选：A．
5．（3分）高速公路的建设带动我国经济的快速发展．在高速公路的建设中，通常要从大山中开挖隧道穿过，把道路取直，以缩短路程．这样做包含的数学道理是（ ）
A．两点确定一条直线
B．两点之间，线段最短
C．两条直线相交，只有一个交点
D．直线是向两个方向无限延伸的
【解答】解：从大山中开挖隧道穿过，把道路取直，使两点处于同一条线段上．
这样做包含的数学道理是：两点之间，线段最短．
故选：B．
6．（3分）如图，在△ABC中，∠BAC＝90°，∠CDA＝90°，则与∠B互为余角的角有（ ）
A．2个B．3个C．4个D．5个
【解答】解：∵∠BAC＝90°，
∴∠BAC+∠CAD＝90°，∠B+∠C＝180°﹣90°＝90°．
∵∠CDA＝90°，
∴∠B+∠BAD＝90°，
即与∠B互余的角有：∠C，∠BAD共2个．
故选：A．
7．（3分）《算学启蒙》中有一道题，原文是：良马日行二百四十里，驽马日行一百二十里．驽马先行一十二日，问良马几何追及之？译文为：跑得快的马每天走240里，跑的慢的马每天走120里．慢马先走12天，快马几天可以追上慢马？设快马x天可以追上慢马，可列方程（ ）
A．240（x+12）＝120xB．240（x﹣12）＝120x
C．240x＝120（x+12）D．240x＝120（x﹣12）
【解答】解：设快马x天可以追上慢马，则慢马跑了（x+12）天，
依题意，得：240x＝120（x+12）．
故选：C．
8．（3分）汉字文化正在走进人们的日常消费生活．如图所示图形都是由同样大小的圆点和线段按照一定的规律排列组成的篆书简化“汉”字，其中，图①中共有12个圆点，图②中共有18个圆点，图③中共有25个圆点，图④中共有33个圆点…依此规律则，图⑩中共有圆点的个数是（ ）
A．63B．75C．88D．102
【解答】解：在图①中，圆点个数y1＝12，
在图②中，圆点个数y2＝18＝6+y1，
在图③中，圆点个数y3＝25＝7+y2，
在图④中，圆点个数y4＝33＝8+y3，
∴y5＝9+y4＝42，y6＝10+y5＝52，y7＝11+y6＝63，y8＝12+y7＝75，y9＝13+y8＝88，y10＝14+y9＝102，
∴图⑩中共有圆点的个数是102，
故选：D．
二．填空题（本大题共10小题，每题3分，共30分）
9．（3分）﹣2的绝对值是 2 ．
【解答】解：﹣2的绝对值是：2．
故答案为：2．
10．（3分）若代数式2xmy2与﹣2xy2n为同类项，则m+n的值为 2 ．
【解答】解：根据题意得：m＝1，2n＝2，
解得m＝1，n＝1，
∴m+n＝1+1＝2．
故答案为：2．
11．（3分）已知∠A＝38°30'，则∠A的补角的大小是 141°30′ ．
【解答】解：∵∠A＝38°30'，
∴∠A的补角＝180°﹣38°30′＝179°60′﹣38°30′＝141°30′，
故答案为：141°30′．
12．（3分）若x＝2是关于x的方程mx+4＝3m的解，则m＝ 4 ．
【解答】解：根据题意，得2m+4＝3m，
解得m＝4，
故答案为：4．
13．（3分）如果2a﹣3b的值为﹣1，则6b﹣4a+1的值为 3 ．
【解答】解：∵2a﹣3b＝﹣1，
∴原式＝﹣2（2a﹣3b）+1
＝﹣2×（﹣1）+1
＝2+1
＝3．
故答案为：3．
14．（3分）一件商品标价140元，若八折出售，仍可获利12%，则这件商品的进价为 100 元．
【解答】解：设这件商品的进价为x元，
由题意得140×80%﹣x＝12%x，
解得x＝100，
答：这件商品的进价为100元．
故答案为100．
15．（3分）已知点C在线段AB上，AB＝8，BC＝2，M是线段AC的中点，则AM的长为 3 ．
【解答】解：∵点C在线段AB上，由线段的和差，得
AC＝AB﹣BC＝8﹣2＝6．
AM＝AC＝×6＝3；
故答案为：3．
16．（3分）如图，将书页的一角斜折过去，使角的顶点A落在A′处，BC为折痕，BD平分∠A′BE，若∠A′BD＝70°，则∠ABC＝ 20° ．
【解答】解：∵BD平分∠A′BE，若∠A′BD＝70°，
∴∠A'BE＝2∠A′BD＝2×70°＝140°，
∴∠ABA'＝180°﹣∠A'BE＝180°﹣140°＝40°，
∵折叠顶点A落在A′处，BC为折痕，
∴∠ABC＝∠A'BC＝×∠ABA'＝×40°＝20°，
故答案为：20°．
17．（3分）若a＜1，|1﹣a|+|3﹣a|＝ 4﹣2a ．
【解答】解：∵a＜1，
∴1﹣a＞0，3﹣a＞0，
∴原式＝1﹣a+3﹣a＝4﹣2a．
故答案为：4﹣2a．
18．（3分）如图1，在一条可以折叠的数轴上有A，B，C三点，其中点A，点B表示的数分别为﹣8和+5，现以点C为折点，将数轴向右对折，点A对应的点A1落在B的右边；如图2，再以点B为折点，将数轴向左折叠，点A1对应的点A2落在B的左边，若A2，B两点之间的距离为2，则B，C两点之间的距离是 5.5 ．
【解答】解：设点C所表示的数为c，则AC＝c+8，BC＝5﹣c，
∵A1B＝2，B点表示的数为5，
∴点A1表示的数为5+2＝7，
根据折叠得，AC＝A1C，
∴c+8＝7﹣c，
解得c＝﹣，
∵B，C两点之间的距离为x，
∴x＝5﹣（﹣）＝5..5．
故答案为：5.5．
三．解答题（本大题共10小题，共96分）
19．（8分）计算：
（1）1.5﹣（﹣3）+2.75﹣（+4）；
（2）﹣32÷3+（+）×6﹣（﹣1）2022．
【解答】解：（1）1.5﹣（﹣3）+2.75﹣（+4）
＝1.5+3+2+（﹣4.5）
＝3；
（2）﹣32÷3+（+）×6﹣（﹣1）2022
＝﹣9÷3+×6﹣1
＝﹣3+7﹣1
＝3．
20．（8分）解方程：
（1）7x+6＝8﹣5x；
（2）＝1﹣．
【解答】解：（1）7x+6＝8﹣5x，
移项得，7x+5x＝8﹣6，
合并同类项得，12x＝2，
系数化为1得，x＝；
（2）＝1﹣，
去分母得，2（2x+1）＝6﹣3（x﹣1），
去括号得，4x+2＝6﹣3x+3，
移项得，4x+3x＝6+3﹣2，
合并同类项得，7x＝7，
系数化为1得，x＝1．
21．（8分）先化简，再求值：2x2﹣[3x﹣2（2x﹣3）+4x2]，其中x＝．
【解答】解：原式＝2x2﹣（3x﹣4x+6+4x2）
＝2x2﹣（﹣x+6+4x2）
＝2x2+x﹣6﹣4x2
＝﹣2x2+x﹣6，
当x＝时，
原式＝﹣2×+﹣6
＝﹣6．
22．（8分）已知方程6x﹣9＝10x﹣5与方程3a﹣1＝3（x+a）﹣2a的解相同；
（1）求这个相同的解；
（2）求a的值．
【解答】解：（1）6x﹣9＝10x﹣5
移项，得：
6x﹣10x＝﹣5+9，
合并同类项，得：
﹣4x＝4，
系数化为1，得：
x＝﹣1．
（2）由方程6x﹣9＝10x﹣5与方程3a﹣1＝3（x+a）﹣2a的解相同，得
3a﹣1＝3（﹣1+a）﹣2a，
解得a＝﹣1．
23．（10分）根据要求完成下列题目：
（1）图中有 8 块小正方体；
（2）请在下面方格纸中分别画出它的左视图和俯视图；
（3）用小正方形体搭一个几何体，使得它的俯视图和左视图与你在如图方格中所画的图一致，则这样的几何最多要 13 个小正方体．
【解答】解：（1）由图可知，该几何体最下面一层有5个小正方体，第2层有2个小正方体，最上面一层有1个小正方体，
故共有5+2+1＝8（块）小正方体．
故答案为：8；
（2）如图所示：
（3）这样的几何体所需正方体最多分布情况如图所示：
共需要正方体13个．
故答案为：13．
24．（10分）如图，O在直线AB上，射线OD平分∠AOC，射线OE在∠BOC内．
（1）若∠DOE＝90°，求证：射线OE是∠BOC的平分线；
（2）若∠COE＝∠EOB，∠DOE＝48°，求∠EOB的度数．
【解答】（1）证明：∵∠DOE＝90°，
∴∠DOC+∠COE＝90°，
∵∠AOB＝180°，
∴∠DOA+∠BOE＝180°﹣∠DOE＝90°，
∵射线OD平分∠AOC，
∴∠DOA＝∠DOC，
∴∠COE＝∠BOE，
∴射线OE是∠BOC的平分线；
（2）解：∵∠COE＝∠EOB，
∴设∠COE＝x，则∠EOB＝3x，
∵∠DOE＝48°，
∴∠DOC＝∠DOE﹣∠COE＝48°﹣x，
∵射线OD平分∠AOC，
∴∠AOC＝2∠DOC＝2（48°﹣x），
∵∠AOC+∠COE+∠BOE＝180°，
∴2（48°﹣x）+x+3x＝180°，
解得：x＝42°，
∴∠EOB＝126°．
25．（10分）在如图所示的方格纸中，每个小正方形的边长为1，每个小正方形的顶点都叫格点，请利用网格特征，解答下列问题
（1）过点C画AB的垂线，并标出垂线所经过的格点E；
（2）过点C画AB的平行线，并标出平行线所经过的格点F；
（3）直线CE与直线CF的位置关系是 CF⊥CE ；
（4）连接AC，BC，则△ABC的面积为 ．
【解答】解：（1）如图所示，CE即为所求；
（2）如图所示，CF即为所求；
（3）∵CE⊥AB，且AB∥CF，
∴CF⊥CE，
故答案为：CF⊥CE．
（4）△ABC的面积为4×4﹣×1×4﹣×1×3﹣×4×3＝，
故答案为：．
26．（10分）扬州树人学校初一年级某班级为了迎接新年，装扮教室，购买了2种气球，气球种类有笑脸和爱心两种．两种气球的价格不同，但同一种类的气球价格相同，由于教室布置需要，购买了的三束气球（每束4个气球），每束价格如图所示．
（1）若笑脸气球的单价是x元，则爱心气球的单价为 元；
（2）请用含x的代数式表示第②束的总价格和第③束气球的总价格；
（3）若第②束气球的总价钱比第③束气球的总价钱少2元，求这两种类的气球的单价．
【解答】解：（1）由第①束气球可知：爱心气球的单价为：（元）；
故答案为：；
（2）∵第②束的价格为：（元），第③束的价格为：（元），
∴第②束的总价格和第③束气球的总价格为：（元）；
（3）∵第②束气球的总价钱比第③束气球的总价钱少2元，
∴，
8x+14﹣4x﹣28＝6，
4x﹣14＝6，
4x＝20，
x＝5，
∴（元）
答：笑脸气球的单价是5元，则爱心气球的单价是3元．
27．（12分）定义：若m+n＝3，则称m与n是关于3的巧数．
（1）1与 2 是关于3的巧数，5﹣x与 x﹣2 是关于3的巧数（填一个含x的代数式）；
（2）若a＝x2+6x﹣1，b＝x2﹣2（x2+3x﹣1）+2，判断a与b是否是关于3的巧数，并说明理由；
（3）若c＝kx﹣1，d＝x﹣4，且c与d是关于3的巧数，若x为正整数，求非负整数k的值．
【解答】解：（1）∵1+2＝3，
∴1与2是关于3的巧数，
∵5﹣x+（x﹣2）＝3，
∴5﹣x与x﹣2是关于3的巧数，
故答案为：2，x﹣2；
（2）x2+6x﹣1+x2﹣2（x2+3x﹣1）+2
＝x2+6x﹣1+x2﹣2x2﹣6x+2+2
＝3，
∴a与b是关于3的巧数；
（3）∵c与d是关于3的巧数，
∴kx﹣1+x﹣4＝3，
∴（k+1）x＝8，
∴x＝，
∵x为正整数，k是非负整数，
∴k+1＝1或k+1＝2或k+1＝4或k+1＝8，
∴k的值为0或1或3或7．
28．（12分）如图，以直线AB上一点O为端点作射线OC，使∠AOC＝48°，在同一个平面内将一个直角三角板的直角顶点放在点O处．（注：∠DOE＝90°）
（1）如图1，如果直角三角板DOE的一边OD放在射线OA上，那么∠COE的度数为 42° ；
（2）如图2，将直角三角板DOE绕点O按顺时针方向转动到某个位置，如果OC恰好平分∠AOE，求∠COD的度数；
（3）如图3，将直角三角板DOE绕点O任意转动，如果OD始终在∠AOC的内部，请直接用等式表示∠AOD和∠COE之间的数量关系．
【解答】解：（1）∠COE＝∠DOE﹣∠AOC＝90°﹣48°＝42°，
故答案为：42°；
（2）∵OC平分∠AOE，∠AOC＝48°，
∴∠COE＝∠AOC＝48°，
∵∠DOE＝90°，
∴∠COD＝∠DOE﹣∠COE＝90°﹣48°＝42°；
（3）∠COE﹣∠AOD＝42°，
理由如下：
当OD始终在∠AOC的内部时，
有∠AOD+∠COD＝48°，∠COE+∠COD＝90°，
∴∠COE﹣∠AOD＝90°﹣48°＝42°，
∴∠COE﹣∠AOD＝42°