






人教版(2024)1.2 有理数说课课件ppt
展开1.借助数轴理解绝对值的几何意义;2.会求有理数的绝对值.3.理解绝对值的非负性,并能解决问题。
从数形两方面理解绝对值的非负性
一般的,互为相反的两个数什么是相同的?
2. 化简下列各数的符号 (1)-(+10) (2)+(-0.15) (3)+(+3) (4)-(-12)
解:(1)-(+10)=-10;
(2)+(-0.15)=-0.15;
(3)+(+3)=3;
(4)-(-12)=12;
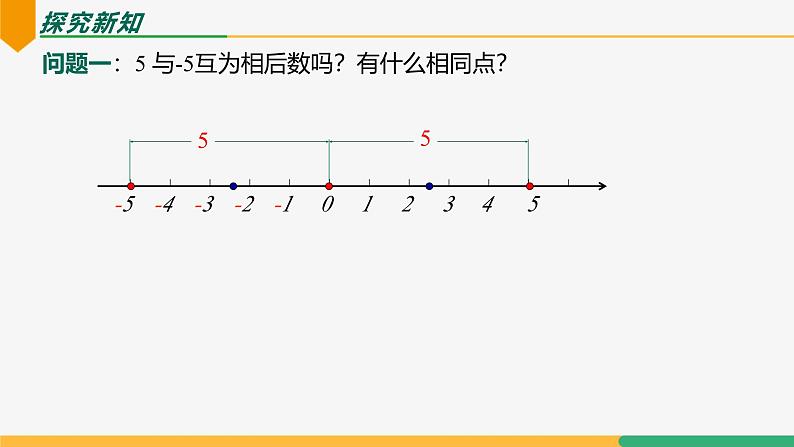
问题一:5 与-5互为相后数吗?有什么相同点?
绝对值的定义 (教材P13)
一般地,数轴上表示数 a的点与原点的距离叫做数 a的绝对值.
思考:1.任何一个数的绝对值一定是什么数?说说理由?2.怎样求一个数的绝对值?
1.任何数的绝对值是非负数. 即:| a |≥0
2.绝对值求法:(1) 一个正数的绝对值是它本身. 若 a >0,则 | a |= a(2) 0 的绝对值是0.(零)若 a =0,则 | a |= 0(3) 一个负数的绝对值是它的相反数.若 a >0,则 | a |= - a
例2 如图1.2-8,数轴上的点A,B,C,D分别表示有理数a,b,c,d,这四个数中,绝对值最小的是哪个数?
例3 已知|x-4 |+|y-3|=0,求x+y的值
解:根据题意可知因为 |x-4|≥0;|y-3|≥0所以 |x-4|=0;|y-3|=0x-4=0,y-3=0,x=4,y=3,所以x+y=7.
形:轴上表示数 a的点与原点的距离
a 绝对值表示为 |a|.
若|a|+|b|=0,则a=0,b=0
一个正数的绝对值是它本身.0 的绝对值是0.一个负数的绝对值是它的相反数
(1)一个数的绝对值是4 ,则这数是-4. (2)|3|>0. (3)|-1.3|>0.(4)有理数的绝对值一定是正数. (5)若a=-b,则|a|=|b|. (6)若|a|=|b|,则a=b.(7)若|a|=-a,则a必为负数. (8)互为相反数的两个数的绝对值相等.
1.判断下列说法是否正确.
2.下列关于|-3|的意义,说法正确的是( ) A.求-3的相反数 B.数轴上表示-3的点到原点的距离C.数轴上表示3的点到原点的距离D.以上都不对
7. (1) 绝对值是3的数有几个?是什么? (2) 绝对值是0的数有几个?是什么? (3) 绝对值是-1的数是否存在?为什么?
有两个,分别是3和-3.
不存在,到原点的距离不能是负数.
初中数学1.2 有理数教案配套课件ppt: 这是一份初中数学<a href="/sx/tb_c4050847_t3/?tag_id=26" target="_blank">1.2 有理数教案配套课件ppt</a>,共29页。PPT课件主要包含了24绝对值,路线不同正负性,绝对值的判断法则,还有0,-88,或-2,绝对值,非负数,非正数等内容,欢迎下载使用。
初中数学1.2 有理数教学ppt课件: 这是一份初中数学<a href="/sx/tb_c4050847_t3/?tag_id=26" target="_blank">1.2 有理数教学ppt课件</a>,共25页。PPT课件主要包含了学习目标及重难点,复习回顾,+10,探索一绝对值的定义,绝对值的定义,显然00,你发现了什么规律吗,探索二绝对值的性质,的绝对值是0,归纳总结等内容,欢迎下载使用。
初中数学人教版(2024)七年级上册(2024)1.2 有理数教案配套课件ppt: 这是一份初中数学人教版(2024)七年级上册(2024)<a href="/sx/tb_c4050847_t3/?tag_id=26" target="_blank">1.2 有理数教案配套课件ppt</a>,共13页。PPT课件主要包含了学习目标,新课引入,C-20°C,B20°C,A0°C,绝对值的概念,探究点1,获取新知,绝对值的性质,探究点2等内容,欢迎下载使用。













