2025高考数学一轮复习-7.2-空间点、直线、平面之间的位置关系【课件】

这是一份2025高考数学一轮复习-7.2-空间点、直线、平面之间的位置关系【课件】，共60页。PPT课件主要包含了知识诊断基础夯实，不在一条直线上，两个点，过该点的公共直线，互相平行，相等或互补，ABC，考点突破题型剖析，BCD，ABD等内容，欢迎下载使用。

ZHISHIZHENDUANJICHUHANGSHI
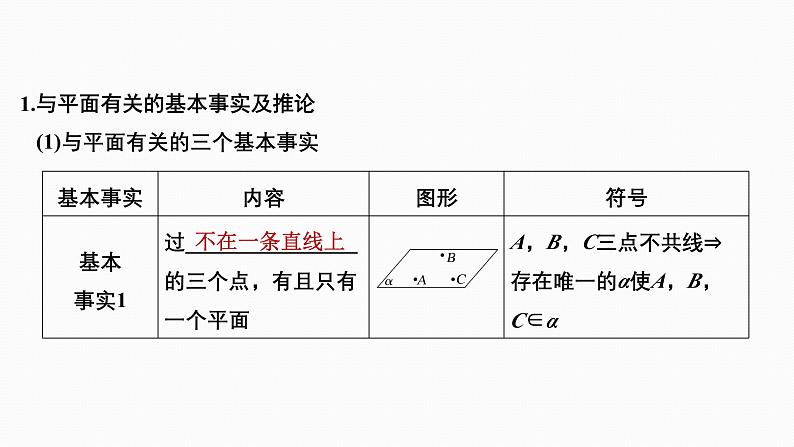
1.与平面有关的基本事实及推论(1)与平面有关的三个基本事实
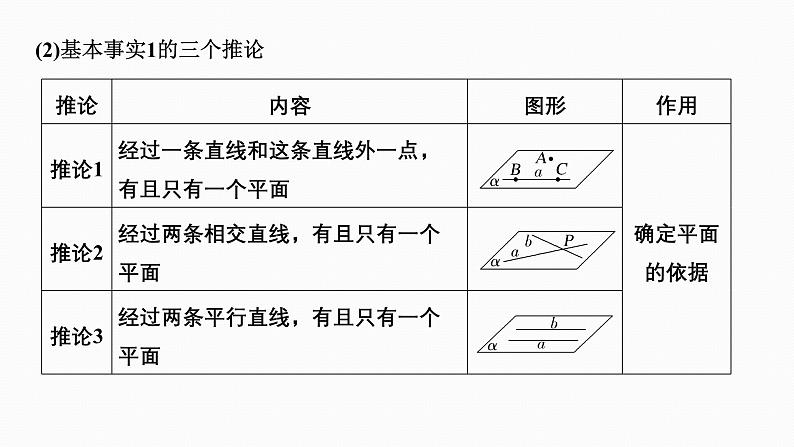
(2)基本事实1的三个推论
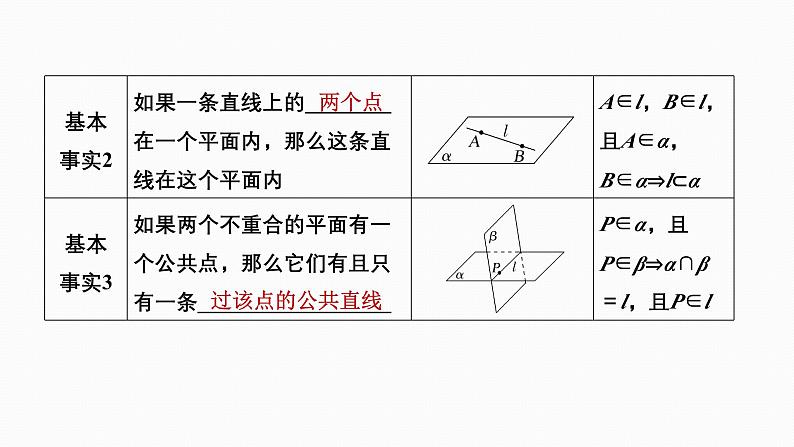
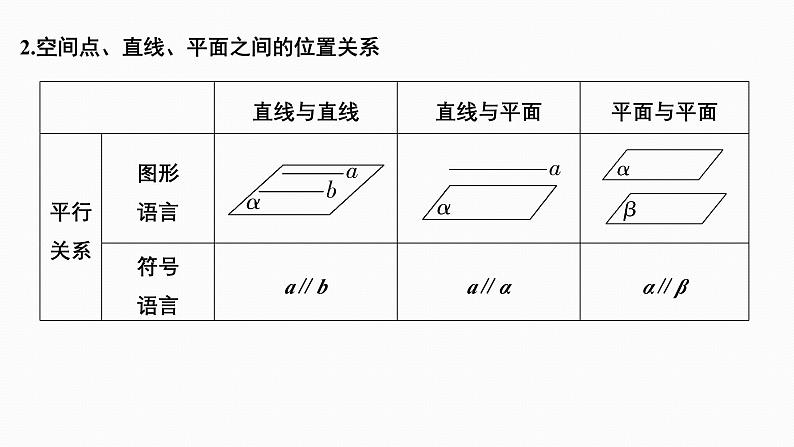
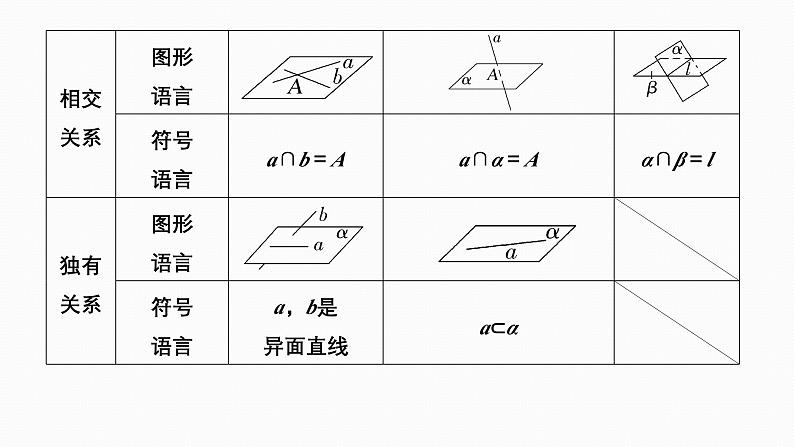
2.空间点、直线、平面之间的位置关系
3.基本事实4和等角定理平行公理：平行于同一条直线的两条直线__________.等角定理：如果空间中两个角的两边分别对应平行，那么这两个角____________.4.异面直线所成的角(1)定义：已知a，b是两条异面直线，经过空间任意一点O作直线a′∥a，b′∥b，把a′与b′所成的角叫做异面直线a与b所成的角(或夹角).
1.证明点共线与线共点都需用到基本事实3.2.两异面直线所成的角归结到一个三角形的内角时，容易忽视这个三角形的内角可能等于两异面直线所成的角，也可能等于其补角.
解析　(1)如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线，故错误.(3)如果两个平面有三个公共点，则这两个平面相交或重合，故错误.(4)由于a不平行于平面α，且a⊄α，则a与平面α相交，故平面α内有与a相交的直线，故错误.
1.思考辨析(在括号内打“√”或“×”)(1)两个平面α，β有一个公共点A，就说α，β相交于过A点的任意一条直线.(　　)(2)两两相交的三条直线最多可以确定三个平面.(　　)(3)如果两个平面有三个公共点，则这两个平面重合.(　　)(4)若直线a不平行于平面α，且a⊄α，则α内的所有直线与a异面.(　　)
解析　依题意，m∩α＝A，n⊂α，∴m与n可能异面、相交(垂直是相交的特例)，一定不平行.
2.(多选)α是一个平面，m，n是两条直线，A是一个点，若m⊄α，n⊂α，且A∈m，A∈α，则m，n的位置关系可能是(　　 )A.垂直 B.相交 C.异面 D.平行
解析　由于l与直线l1，l2分别共面，故直线l与l1，l2要么都不相交，要么至少与l1，l2中的一条相交.若l∥l1，l∥l2，则l1∥l2，这与l1，l2是异面直线矛盾.故l至少与l1，l2中的一条相交.
3.若直线l1和l2是异面直线，l1在平面α内，l2在平面β内，l是平面α与平面β的交线，则下列命题正确的是(　　)A.l与l1，l2都不相交B.l与l1，l2都相交C.l至多与l1，l2中的一条相交D.l至少与l1，l2中的一条相交
解析　如图，连接BE，因为AB∥CD，所以异面直线AE与CD所成的角等于相交直线AE与AB所成的角，即为∠EAB.
4.在正方体ABCD－A1B1C1D1中，E为棱CC1的中点，则异面直线AE与CD所成角的正切值为(　　)
解析　∵AB⊂γ，M∈AB，∴M∈γ.又α∩β＝l，M∈l，∴M∈β.根据基本事实3可知，M在γ与β的交线上.同理可知，点C也在γ与β的交线上.
5.如图，α∩β＝l，A，B∈α，C∈β，且C∉l，直线AB∩l＝M，过A，B，C三点的平面记作γ，则γ与β的交线必通过(　　)A.点A B.点BC.点C但不过点M D.点C和点M
解析　连接MP，AC(图略)，因为MP∥AC，MP≠AC，所以AP与CM是相交直线，又面A1ADD1∩面C1CDD1＝DD1，所以AP，CM，DD1相交于一点，则A不正确，B正确.
6.(多选)如图，在正方体ABCD－A1B1C1D1中，M，N，P分别是C1D1，BC，A1D1的中点，下列结论正确的是(　　)A.AP与CM是异面直线B.AP，CM，DD1相交于一点C.MN∥BD1D.MN∥平面BB1D1D
令AC∩BD＝O，连接OD1，ON.因为M，N分别是C1D1，BC的中点，
则四边形MNOD1为平行四边形，所以MN∥OD1，因为MN⊄平面BD1D，OD1⊂平面BD1D，所以MN∥平面BD1D，C不正确，D正确.
KAODIANTUPOTIXINGPOUXI
证明　∵EF是△D1B1C1的中位线，∴EF∥B1D1.在正方体AC1中，B1D1∥BD，∴EF∥BD.∴EF，BD确定一个平面，即D，B，F，E四点共面.
例1 如图所示，已知在正方体ABCD－A1B1C1D1中，E，F分别为D1C1，C1B1的中点，AC∩BD＝P，A1C1∩EF＝Q.求证：(1)D，B，F，E四点共面；
(2)若A1C交平面DBFE于R点，则P，Q，R三点共线.证明　在正方体AC1中，设平面A1ACC1为α，平面BDEF为β.∵Q∈A1C1，∴Q∈α.又Q∈EF，∴Q∈β，则Q是α与β的公共点，同理，P是α与β的公共点，∴α∩β＝PQ.又A1C∩β＝R，∴R∈A1C.∴R∈α，且R∈β，则R∈PQ，故P，Q，R三点共线.
证明　因为K∈EH，EH⊂平面ABD，所以K∈平面ABD，同理K∈平面CBD，而平面ABD∩平面CBD＝BD，因此K∈BD，所以EH，BD，FG三条直线相交于同一点.
训练1 如图，在空间四边形ABCD中，E，F分别是AB和BC上的点，G，H分别是CD和AD上的点.若EH与FG相交于点K.求证：EH，BD，FG三条直线相交于同一点.
解析　根据条件作出示意图，容易得到以下三种情况均有可能，
例2 (1)空间中有三条线段AB，BC，CD，且∠ABC＝∠BCD，那么直线AB与CD的位置关系是(　　)A.平行B.异面C.相交或平行D.平行或异面或相交均有可能
如图可知AB，CD有相交，平行，异面三种情况，故选D.
(2)(多选)如图是正四面体的平面展开图，G，H，M，N分别为DE，BE，EF，EC的中点，则在这个正四面体中(　　 )A.GH与EF平行B.BD与MN为异面直线C.GH与MN成60°角D.DE与MN垂直
解析　还原成正四面体A－DEF，如图所示，其中H与N重合，A，B，C三点重合，易知GH与EF异面，BD与MN异面.连接GM，∵△GMH为等边三角形，∴GH与MN成60°角.由图易得DE⊥AF，又MN∥AF，∴MN⊥DE，因此正确的选项是B，C，D.
解析　如图所示，取PB的中点H，连接MH，HC，
训练2 (1)(多选)四棱锥P－ABCD的所有棱长都相等，M，N分别为PA，CD的中点，下列说法正确的是(　　 )A.MN与PD是异面直线B.MN∥平面PBCC.MN∥ACD.MN⊥PB
由题意知，四边形MHCN为平行四边形，且MN∥HC，所以MN∥平面PBC，设四边形MHCN确定平面α，又D∈α，故M，N，D共面，但P∉平面α，D∉MN，因此MN与PD是异面直线；故A，B说法均正确.
若MN∥AC，由于CH∥MN，则CH∥AC，事实上AC∩CH＝C，C说法不正确；因为PC＝BC，H为PB的中点，所以CH⊥PB，又CH∥MN，所以MN⊥PB，D说法正确.
解析　连接D1E并延长，与AD交于点M，由A1E＝2ED，可得M为AD的中点，
(2)如图，在正方体ABCD－A1B1C1D1中，点E，F分别在A1D，AC上，且A1E＝2ED，CF＝2FA，则EF与BD1的位置关系是(　　)A.相交但不垂直 B.相交且垂直C.异面 D.平行
连接BF并延长，交AD于点N，因为CF＝2FA，可得N为AD的中点，
解析　如图，连接C1P，因为ABCD－A1B1C1D1是正方体，且P为B1D1的中点，所以C1P⊥B1D1，
例3 (1)在正方体ABCD－A1B1C1D1中，P为B1D1的中点，则直线PB与AD1所成的角为(　　)
又C1P⊥BB1，B1D1∩BB1＝B1，B1D1，BB1⊂平面B1BP，所以C1P⊥平面B1BP.
又BP⊂平面B1BP，所以有C1P⊥BP.连接BC1，则AD1∥BC1，所以∠PBC1为直线PB与AD1所成的角.
设正方体ABCD－A1B1C1D1的棱长为2，
(2)将正方形ABCD沿对角线AC折起，并使得平面ABC垂直于平面ACD，直线AB与CD所成的角为(　　)A.90° B.60° C.45° D.30°
解析　如图，取AC，BD，AD的中点，分别为O，M，N，
则ON∥CD，MN∥AB，
所以∠ONM或其补角即为所求的角.
因为平面ABC垂直于平面ACD，平面ABC∩平面ACD＝AC，BO⊥AC，AC⊂平面ACD，所以BO⊥平面ACD，所以BO⊥OD.
所以ON＝MN＝OM＝1.所以△OMN是等边三角形，∠ONM＝60°.所以直线AB与CD所成的角为60°.
易知AD1∥DE1，则∠B1DE1为异面直线AD1与DB1所成角.
解析　法一　如图，补上一相同的长方体CDEF－C1D1E1F1，连接DE1，B1E1.
在△B1DE1中，由余弦定理，
法二　如图，连接BD1，交DB1于O，取AB的中点M，连接DM，OM，
易知O为BD1的中点，所以AD1∥OM，则∠MOD为异面直线AD1与DB1所成角.
于是在△DMO中，由余弦定理，
解析　如图，取B1C1的中点D1，连接A1D1，则AD∥A1D1，∠CA1D1(或其补角)就是异面直线A1C与AD所成的角.
连接D1C.∵A1B1＝A1C1，∴A1D1⊥B1C1，又A1D1⊥CC1，B1C1∩CC1＝C1，∴A1D1⊥平面BCC1B1，
∴∠CA1D1＝60°.
∵D1C⊂平面BCC1B1，∴A1D1⊥D1C，∴△A1D1C为直角三角形，
立体几何中的截线、截面问题
利用平面的性质确定截面的形状是解决问题的关键.(1)作截面应遵循的三个原则：①在同一平面上的两点可引直线；②凡是相交的直线都要画出它们的交点；③凡是相交的平面都要画出它们的交线.(2)作交线的方法有如下两种：①利用基本事实3作交线；②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行，然后根据性质作出交线.
设直线C1M，CD相交于点P，直线C1N，CB相交于点Q，连接PQ交直线AD于点E，交直线AB于点F，则五边形C1MEFN为所求截面图形.
解析　先确定截面上的已知边与几何体上和其共面的边的交点，再确定截面与几何体的棱的交点.
(2)已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为(　　)
解析　如图，依题意，平面α与棱BA，BC，BB1所在直线所成角都相等，容易得到平面AB1C符合题意，进而所有平行于平面AB1C的平面均符合题意.
由对称性，知过正方体ABCD－A1B1C1D1中心的截面面积应取最大值，此时截面为正六边形EFGHIJ.
解析　如图，设B1C1的中点为E，球面与棱BB1，CC1的交点分别为P，Q，连接DB，D1B1，D1P，D1Q，D1E，EP，EQ，由∠BAD＝60°，AB＝AD，
知△ABD为等边三角形，∴D1B1＝DB＝2，∴△D1B1C1为等边三角形，
∴P，Q分别为BB1，CC1的中点，
连接EF，A1B，连接A1C1，B1D1交于点M，连接B1E，BC1交于点N，由EF∥B1D1，即E，F，B1，D1共面，由P是线段A1B上的动点，当P重合于A1或B时，C1A1，C1B与平面D1EF的交点分别为M，N，即Q的轨迹为MN，
由A1B＝BC1＝A1C1，得∠A1C1B＝60°，
FENCENGXUNLIAN GONGGUTISHENG
解析　若直线a，b异面，b，c异面，则a，c相交、平行或异面；若a，b相交，b，c相交，则a，c相交、平行或异面；若a⊥b，b⊥c，则a，c相交、平行或异面；由异面直线所成的角的定义知C正确.
1.a，b，c是两两不同的三条直线，下面四个命题中，真命题是(　　)A.若直线a，b异面，b，c异面，则a，c异面B.若直线a，b相交，b，c相交，则a，c相交C.若a∥b，则a，b与c所成的角相等D.若a⊥b，b⊥c，则a∥c
2.给出以下四个命题：①依次首尾相接的四条线段必共面；②过不在同一条直线上的三点，有且只有一个平面；③空间中如果一个角的两边与另一个角的两边分别平行，那么这两个角必相等；④垂直于同一直线的两条直线必平行.其中正确命题的个数是(　　)A.0 B.1 C.2 D.3
解析　①中，空间四边形的四条线段不共面，故①错误；②中，由基本事实1知道，过不在同一条直线上的三点，有且只有一个平面，故②正确；③中，由空间角的等角定理知，空间中如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补，故③错误；④中，空间中，垂直于同一直线的两条直线可相交，可平行，可异面，故④错误.
解析　图A中，直线GH∥MN；图B中，G，H，N三点共面，但M∉平面GHN，N∉GH，因此直线GH与MN异面；图C中，连接MG，GM∥HN，因此GH与MN共面；图D中，G，M，N共面，但H∉平面GMN，G∉MN，因此GH与MN异面.
3.(多选)下图中，G，N，M，H分别是正三棱柱(两底面为正三角形的直棱柱)的顶点或所在棱的中点，则表示直线GH，MN是异面直线的图形有(　　)
解析　∵M∈A1C，A1C⊂平面A1ACC1，∴M∈平面A1ACC1，又∵M∈平面AB1D1，∴M在平面AB1D1与平面A1ACC1的交线AO上，即A，M，O三点共线，∴A，M，O，A1共面且A，M，C，O共面，∵平面BB1D1D∩平面AB1D1＝B1D1，∴M在平面BB1D1D外，即B，B1，O，M不共面，故选A，B，C.
4.(多选)如图所示，在正方体ABCD－A1B1C1D1中，O是B1D1的中点，直线A1C交平面AB1D1于点M，则下列结论正确的是(　　 )A.A，M，O三点共线 B.A，M，O，A1共面C.A，M，C，O共面 D.B，B1，O，M共面
A.E，F，G，H四点共面B.FG∥平面ADCC.若直线FG，HE交于点P，则P，A，C三点共线D.若△ABD的面积为6，则△BCD的面积为3
因此E，F，G，H共面，A项正确；假设FG∥平面ADC成立，因为平面ABC∩平面DAC＝AC，
因为FG⊂平面ABC，P∈FG，所以P∈平面ABC，同理P∈平面ADC，因为平面ABC∩平面ADC＝AC，所以P∈AC，所以P，A，C三点共线，因此C正确；
解析　延长AN，与CC1的延长线交于点P，则P∈平面BB1C1C，连接PM，与B1C1交于点E，连接NE，
6.我国古代的数学著作《九章算术·商功》中，将底面是直角三角形的直三棱柱称为“堑堵”.在如图所示的“堑堵”ABC－A1B1C1中，AB＝AC＝AA1＝2，M、N分别是BB1和A1C1的中点，则平面AMN截“堑堵”ABC－A1B1C1所得截面图形的面积为(　　)
得到的四边形AMEN是平面AMN截“堑堵”ABC－A1B1C1所得截面图形，
∴△AMN中MN边上的高
∴AMN截“堑堵”ABC－A1B1C1所得截面图形的面积
解析　因为AB∥CD，由图可以看出EF平行于正方体左右两个侧面，与另外四个侧面相交.
7.如图，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，则直线EF与正方体的六个面所在的平面相交的平面个数为________.
解析　如图所示，设正方体的表面ABB1A1的中心为P，容易证明OP∥A1D，所以直线l即为直线OP，角θ即∠POC1.
8.在正方体ABCD－A1B1C1D1中，点O是底面ABCD的中心，过O点作一条直线l与A1D平行，设直线l与直线OC1的夹角为θ，则cs θ＝________.
设正方体的棱长为2，则
解析　如图，过点B作BM∥C1E交B1C1于点M，过点M作BD的平行线，交C1D1于点N，连接DN，则平面BDNM即为符合条件的平面α，
9.在正方体ABCD－A1B1C1D1中，E是BC的中点，平面α经过直线BD且与直线C1E平行，若正方体的棱长为2，则平面α截正方体所得的多边形的面积为________.
由图可知M，N分别为B1C1，C1D1的中点，
∴等腰梯形MNDB的高为
证明　由已知FG＝GA，FH＝HD，
∴四边形BCHG为平行四边形.
由(1)知BG綉CH，∴EF∥CH，∴EF与CH共面.又D∈FH，∴C，D，F，E四点共面.
(2)C，D，F，E四点是否共面？为什么？
解　由已知可求得正方形ABCD的面积S＝4，所以四棱锥O－ABCD的体积
11.如图，在四棱锥O－ABCD中，底面ABCD是边长为2的正方形，OA⊥底面ABCD，OA＝2，M为OA的中点.(1)求四棱锥O－ABCD的体积；
即DE2＋EM2＝MD2，
(2)求异面直线OC与MD所成角的正切值.解　如图，连接AC，设线段AC的中点为E，连接ME，DE，又M为OA中点，
则∠EMD(或其补角)为异面直线OC与MD所成的角，
∴△DEM为直角三角形，且∠DEM＝90°，
解析　如图，分别取BC，AA1，CC1的中点为H，M，N，连接EH，HN，GN，FM，ME，容易得出FG∥EH，GN∥ME，HN∥FM，
12.如图，正方体ABCD－A1B1C1D1的棱长为1，E，F，G分别为棱AB，A1D1，C1D1的中点，经过E，F，G三点的平面被正方体所截，则截面图形的面积为(　　)
则点E，F，G，H，M，N共面，
即经过E，F，G三点的截面图形为正六边形EHNGFM.连接MN，EG，FH，且相交于点O，
连接AO1，O1D，OD，O1E，OE，
解析　如图，设△BDC的中心为O1，球O的半径为R，
在Rt△OO1D中，R2＝3＋(3－R)2，解得R＝2，
∵BD＝3BE，DE＝2，在△DEO1中，
过点E作球O的截面，当截面与OE垂直时，截面圆的面积最小，
解　∵正方形ABCD的边长为4，且△PAB为等边三角形，E为AB的中点，
14.如图，在四棱锥P－ABCD中，底面ABCD为正方形，边长为4，E为AB的中点，PE⊥平面ABCD.(1)若△PAB为等边三角形，求四棱锥P－ABCD的体积；
又PE⊥平面ABCD，
(2)若CD的中点为F，PF与平面ABCD所成角为45°，求PC与AD所成角的正切值.
解　∵AD∥BC，∴∠PCB即PC与AD所成的角.如图，连接EF，∵PE⊥平面ABCD，EF，BC⊂平面ABCD，
∴PE⊥EF，PE⊥BC，又PF与平面ABCD所成角为45°，即∠PFE＝45°，∴PE＝EF·tan ∠PFE＝4，